汽车使用性能与试验-随机振动基本概念

1.随机过程

事物的运动过程有确定性过程和随机过程两类。前者可以用函数关系式精确描述；而随机变化规律却不能用确定的函数关系式表达。

如在某一公路上行驶的汽车，由于随机因素（如路面高低不平）的影响，路面对汽车产生的激励每时每刻都在变动，并围绕某一平均值上下波动，如图7-3所示。平顺性分析所讨论的随机过程，都具有平稳的可用一个样本函数代表整个过程的各态历经性，这就给平顺性分析带来了很大的便利。

2.加速度均方根值

对于具有各态历经性的平稳随机过程，样本函数X（t）时刻都在变化，其均方根值为

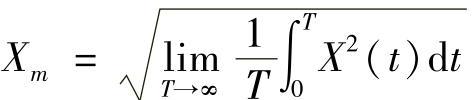
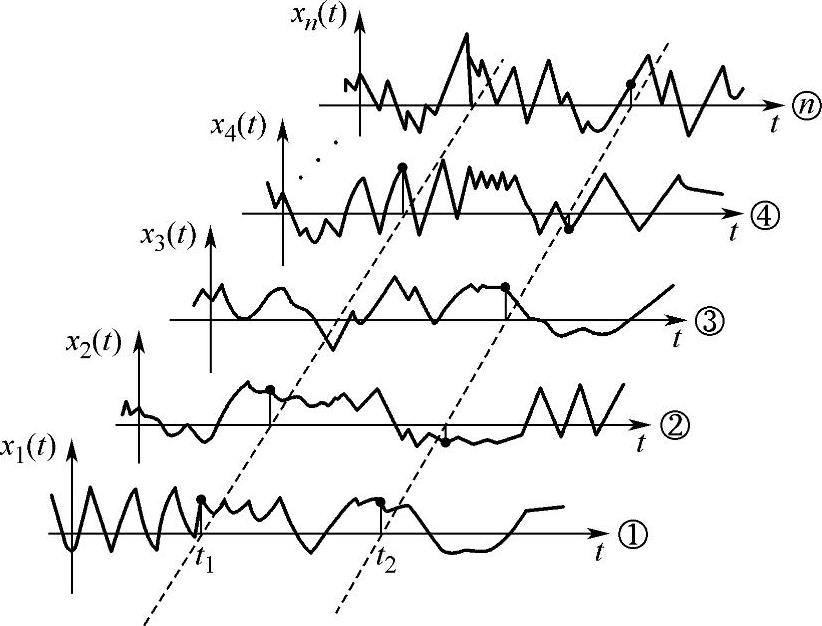
图7-3 随机过程

如果X（t）表示振动的加速度α（t），那么X_m就是加速度均方根值a。

3.功率谱密度

在平顺性分析中，需要利用傅里叶变换作为工具确定时间（或空间）函数的频率结构，并得到频率f的函数G_x（f），反映不同频率上的振动能量和振幅，代表单位频带上所具有的平均功率，即平均功率密度，被称为功率谱密度函数，简称谱密度。谱密度与均方根值之间的关系式为

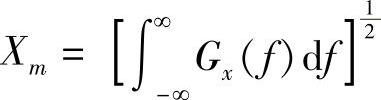
所以，谱密度可用以表示一个系统受到的激励及其响应。

4.1/3倍频带

由数学分析的理论可知，随机过程这样的非周期函数可以看成是频率连续变化的周期函数叠加而成的，即随机过程的样本函数X（t）实际上包含了频率连续变化的周期性函数成分。为了分析方便，常将连续频率按一定规则划分成一些频段，这些频段被称为频带，频带所表示的频率范围称为频带宽，如图7-4所示，每个频带由其中心频率f_c表示，频带宽Δf为

Δf=f_u-f_l(https://www.daowen.com)

式中 f_u——上限频率；

f_l——下限频率。

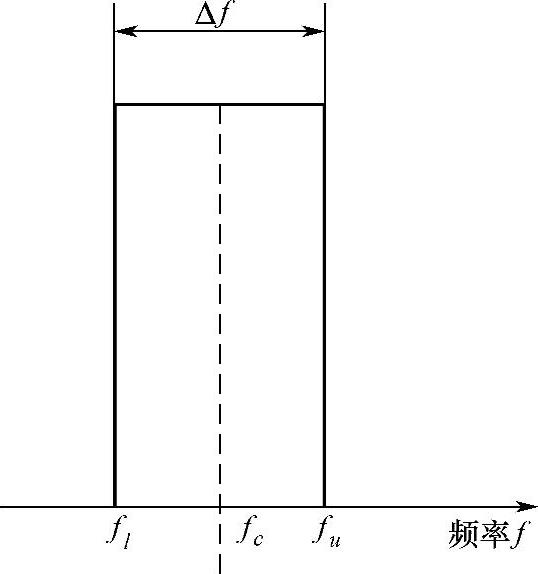
图7-4

若每个频带范围按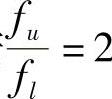确定，这样的频带称为“倍频带”，把“倍频带”按等比关系分成三个频带，称为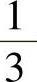倍频带，此时：

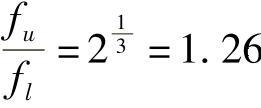
其中心频率为

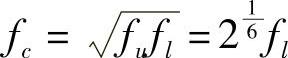
5.常系数线性系统

在汽车平顺性研究中，通常将汽车近似看成常系数线性系统。所谓常系数，是指系统的质量、刚度和阻尼等不随时间变化；而所谓线性，则是指能够满足叠加原理，其运动微分方程是线性常系数微分方程。对于线性系统来说，系统的固有传递特性，不会因激励的不同而变化，若输入是频率为f的正弦波，输出也必然是同频率的正弦波。

6.频响函数

对于一个振动系统，输出与输入的幅值比和相位角反映了系统的传递特性，取决于系统固有的参数。一个复数具有模和相角两个参数，因此一个系统的传递特性可以用一个复数H（jω）表示，称H（jω）为频率响应函数，简称频响函数。频响函数与输入、输出之间有如下十分重要的关系：

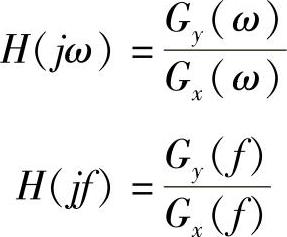
式中 G_y——输出功率谱密度；

G_x——输入功率谱密度。