计算二重极限的几种方法
苏燕玲
1 利用函数的四则运算性质及函数的连续性求极限
由于多元初等函数在其定义区域上是连续的,结合多元函数的四则运算与复合运算,定义区域内各点处的极限等于函数在该点的函数值。
例1 求极限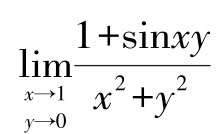
解:由于函数f(x,y)=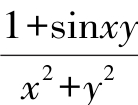 是多元初等函数,点(1,0)是函数f(x, y)定义区域内的点,所以函数在该点连续,故
是多元初等函数,点(1,0)是函数f(x, y)定义区域内的点,所以函数在该点连续,故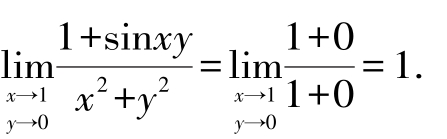
例2 求极限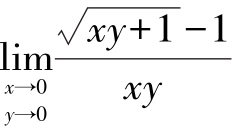
解:对函数有理化后有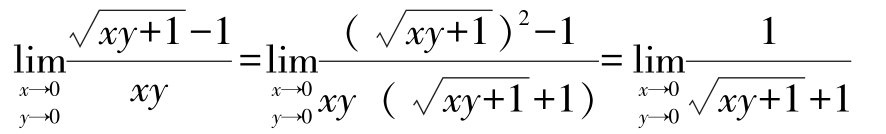
而函数在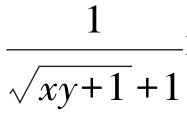
在(0,0)点连续,所以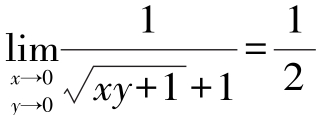
2 利用无穷小性质求极限(一元函数关于无穷小性质求极限的方法可以推广到多元函数)
例3 求极限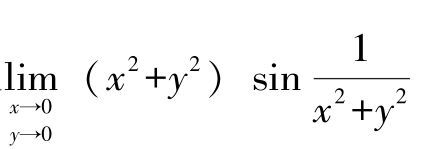
解:由于x2+y2在(x,y)→(0,0)时是无穷小,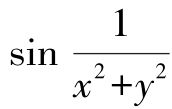 是有界变量,
是有界变量,
所以
这里用到了有界变量与无穷小量的乘积仍为无穷小的性质,注意这里使用一元函数关于无穷小性质求极限的方法时,已经将多元函数转化为一元函数。
例4 求极限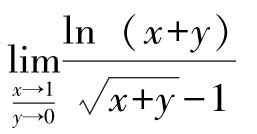
解:当(x,y)→(1,0)时,ln(x+y)→0,所以ln(x+y)~[(x+y)-1]
于是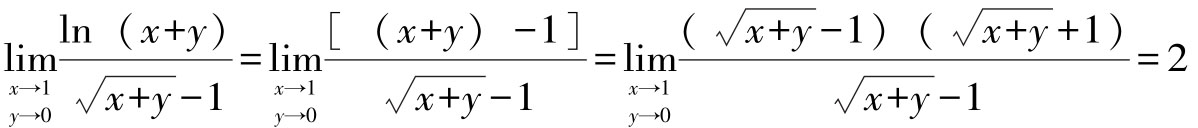
例5 求极限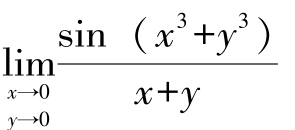
解:当(x,y)→(0,0)时,sin(x3+y3)~(x3+y3)
于是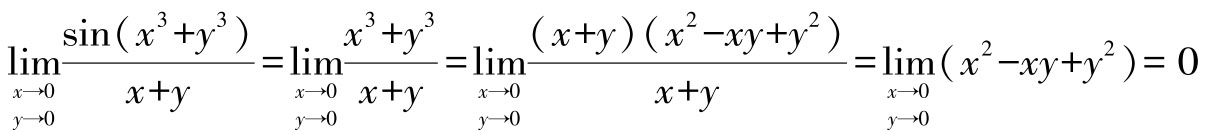
这里例4、例5都用到等价无穷小替换的性质。
3 用夹逼准则求极限
例6 求极限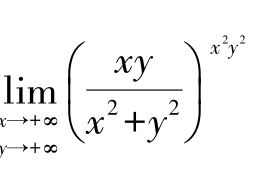
解:因为x2+ y2≥2xy,x> 0,y> 0,所以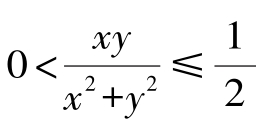 ,从而
,从而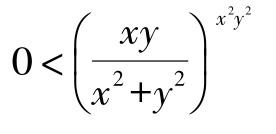
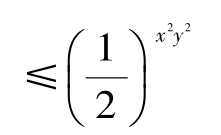
例7 求极限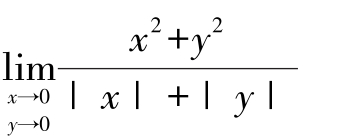
解:因为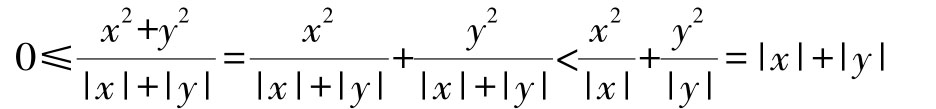
而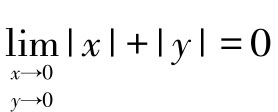 ,所以
,所以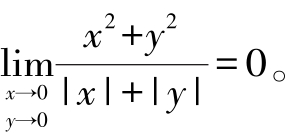
4 通过变量替换化为一元函数求极限
例8 求极限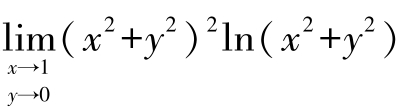
解:令t= x2+y2,则(x,y)→(0,0)时,t→0
所以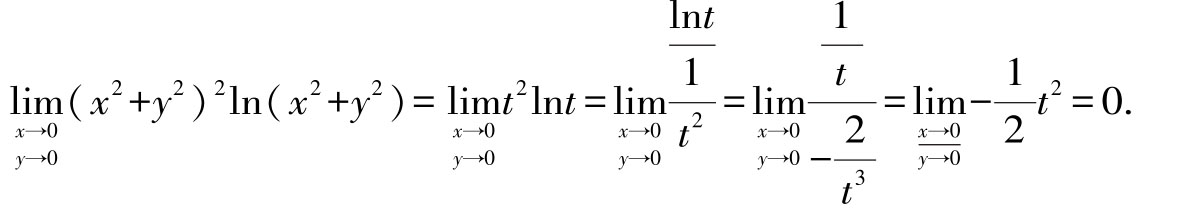
只有通过变量替换将二元函数化为一元函数,罗比达法则才可以使用,也就是说不能对二元函数直接使用罗比达法则求极限。
5 利用取对数求极限
例9 求极限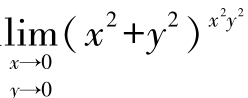 。
。
解:此极限为幂指函数的极限,令u=(x2+y2)x2y2,则ln u= x2 y2 ln(x2+y2)(https://www.daowen.com)
又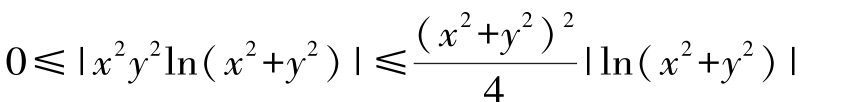
再令t= x2+y2,则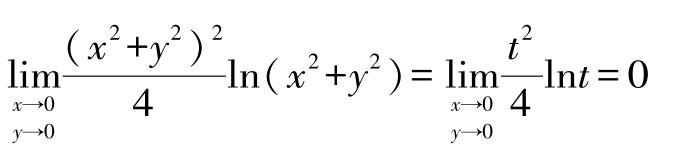
所以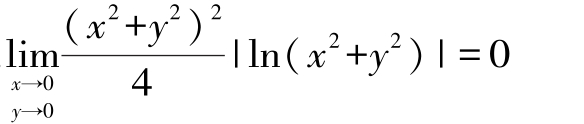
由夹逼准则得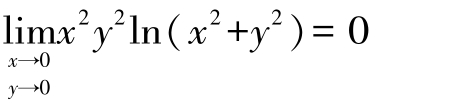
所以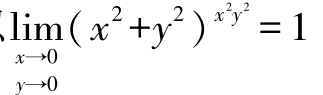
6 通过简单变形求极限
例10 求极限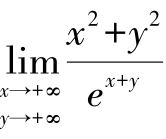
解:注意到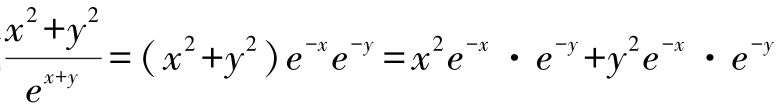
又x2 e-x→0(x→+∞),e-y→0(y→+∞)
所以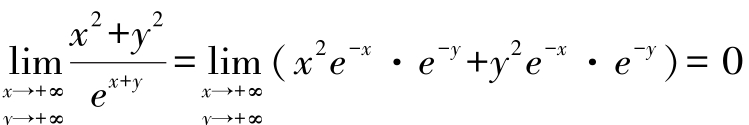
例11 求极限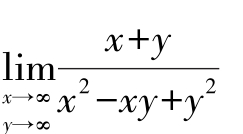 解:由于
解:由于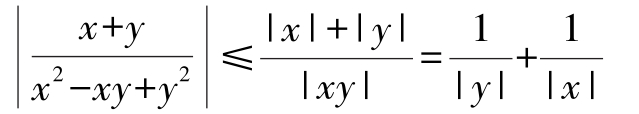
而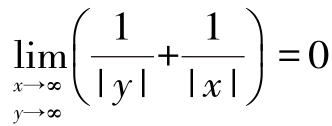 ,所以
,所以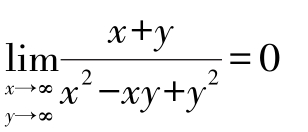
7 用极坐标求极限
若(x,y)→(0,0)时,二元函数中含有x2+ y2,可以考虑极坐标变换法,即令x= r cosθ,y= r sinθ,将f(x,y)的极限问题转换为f(r,θ)的极限问题,但要注意用极坐标求极限时极限过程要适用θ的所有取值。
例12 求极限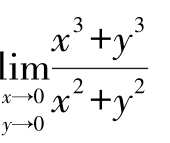
解:令x= r cosθ,y= r sinθ,则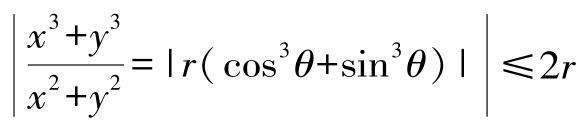
当(x,y)→(0,0)时,r→0又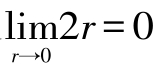 ,所以
,所以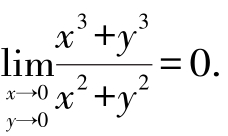
8 用定义求极限
例13 求极限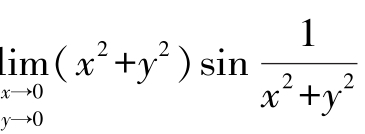
解:因为∀ε>0,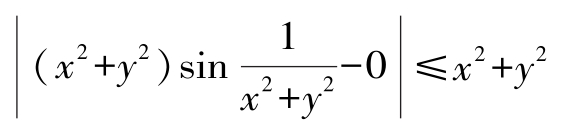
只须取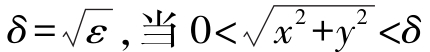 时
时
总有x2+y2<ε,即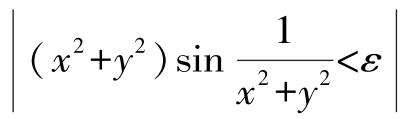
所以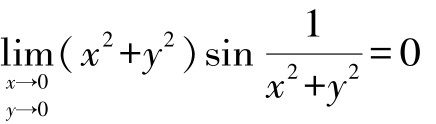
9 极限不存在情况的判断
多元函数极限不存在的判断一般可以从以下两个方面考虑,当点p(x,y)沿着直线y= kx趋于(0,0)点时,如果极限不存在或者极限与k值有关,则极限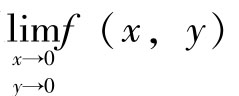 不存在;如果点p(x,y)沿着直线y= kx趋于(0,0)点时,极限存在且与k值无关,这时还不能判断极限存在,需要考虑点p(x,y)沿着不同的曲线趋于(0,0)点时的变化趋势,即找两种不同的曲线,如果其中一种曲线极限不存在或者两种曲线极限都存在但不相等,则极限
不存在;如果点p(x,y)沿着直线y= kx趋于(0,0)点时,极限存在且与k值无关,这时还不能判断极限存在,需要考虑点p(x,y)沿着不同的曲线趋于(0,0)点时的变化趋势,即找两种不同的曲线,如果其中一种曲线极限不存在或者两种曲线极限都存在但不相等,则极限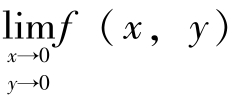 不存在。
不存在。
例14 判断极限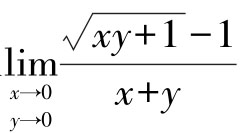 是否存在.
是否存在.
解:很显然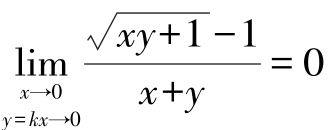 ,但这并不能说明极限存在,也不能说明极限不存在,因为
,但这并不能说明极限存在,也不能说明极限不存在,因为
考虑曲线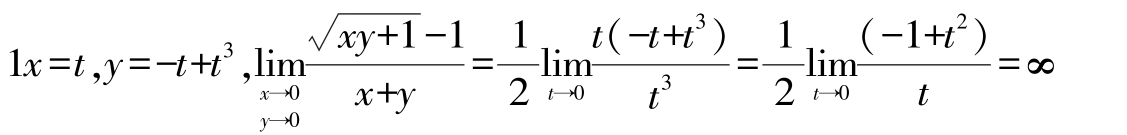
考虑曲线2 x= t,y= t+t3,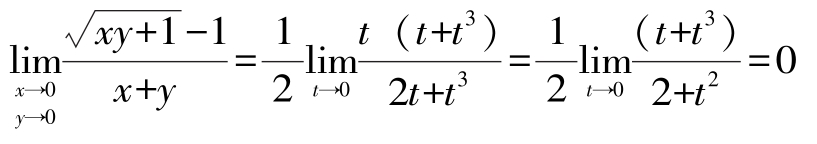
所以极限不存在。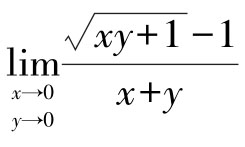
参考文献
[1]同济大学应用数学系主编.高等数学(第六版).高等教育出版社出版.
[2]华东示范大学数学系主编.数学分析(第三版).高等教育出版社出版.
[3]朱来义主编.微积分中的典型例题分析与习题(第一版).高等教育出版社出版.
[4]辛春元.二重极限计算方法的研究.长春教育学院学报,2011(7).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






