答 案
移动8次
(1)在大正方形内取出12根火柴,将它们摆成新的相同正方形,如图1—01;
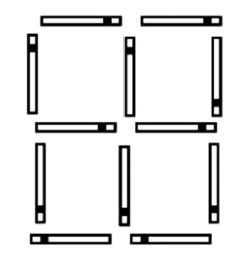
图1—01
(2)见图1—02;
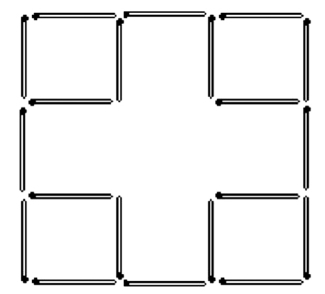
图1—02
(3)见图1—03a、b和c。去掉4根火柴如图a;去掉6根火柴如图b;去掉8根火柴如图c。
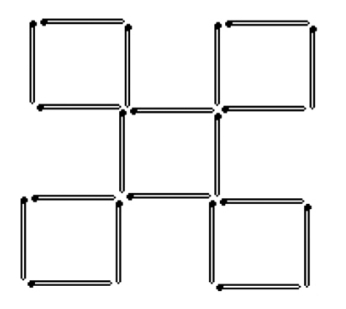
图1—03a
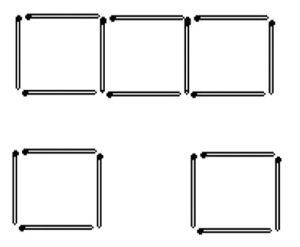
图1—03b
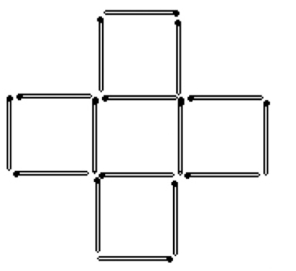
图1—03c
(4)见图1—04a、b。
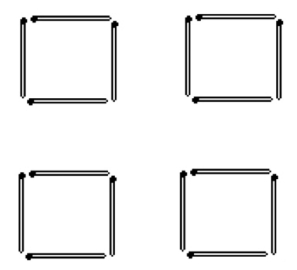
图1—04a
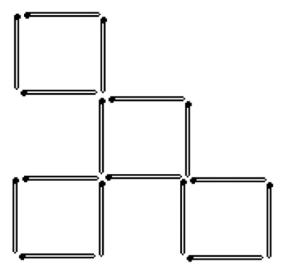
图1—04b
(5)见图1—05。
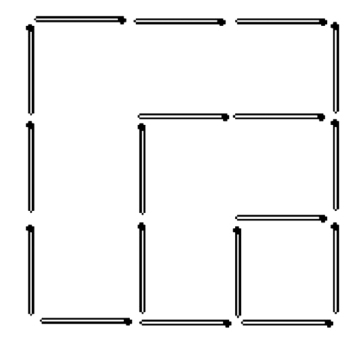
图1—05
(6)见图1—06a、b。
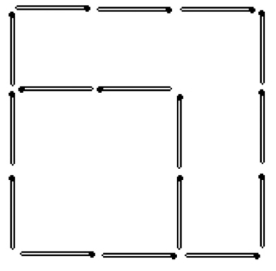
图1—06a
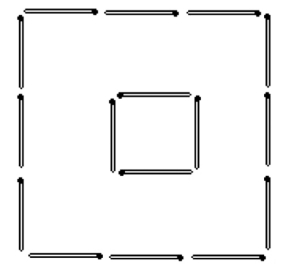
图1—06b
(7)见图1—07。
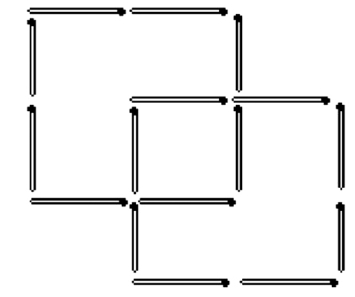
图1—07
(8)见图1—08。
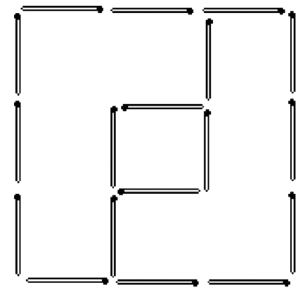
图1—08
螺旋变三角形
详见图1—09。
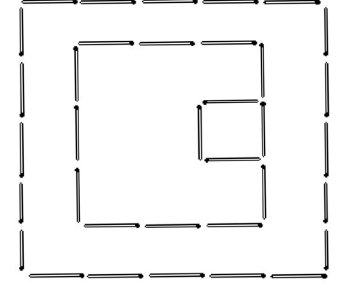
图1—09
房子变正方形
见图1—10。重摆两根如图a,重摆4根如图b。
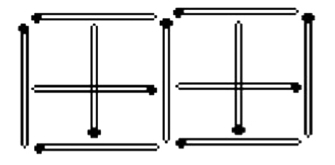
图1—10a
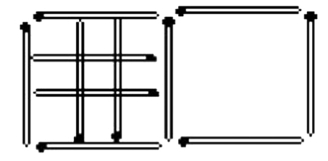
图1—10b
至少拿掉几根
见图1—11,至少取出9根火柴。
图1—11
搭 桥
详见图1—12。
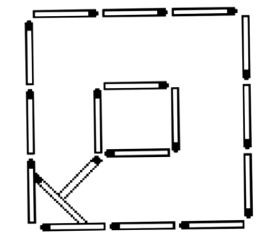
图1—12
变幻的箭
详见图1—13a、b,a为重摆8根火柴,b为重摆7根火柴。
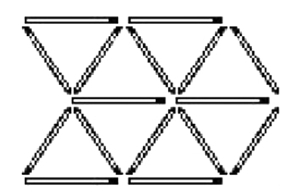
图1—13a
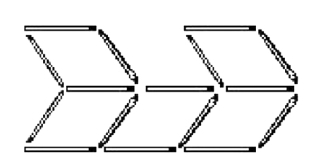
图1—13b
有水井的花园
详见图1—14a、b。
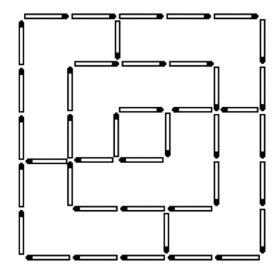
图1—14a

图1—14b
等边三角形
详见图1—15,可连接成7个等边三角形,若仅限于平面,则无解。
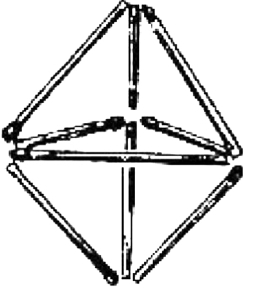
图1—15
先拿哪一根
先拿头朝向硬币的右绕第五根火柴(头朝向硬币火柴不算)。
每列3个
三个棋子一列的共有8列,详见图1—16a;两个棋子一列的共有12列,详见图1—16b;如果去掉三个棋子后,把剩下的六个棋子摆成三角形,详见图1—16c,则每列有三个棋子。
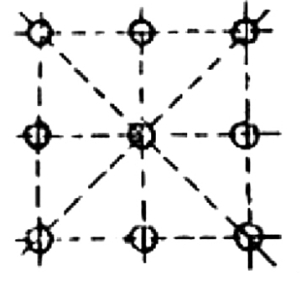
图1—16a
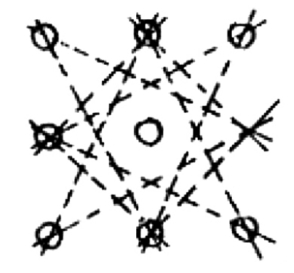
图1—16b
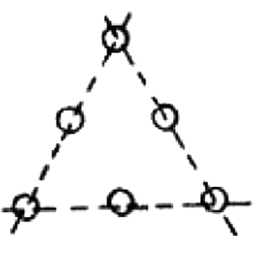
图1—16c
8个棋子
只有一答案,如图1—17所示。不能乱摆,摆的规律是:在第二纵行方格从上至下考虑在一方格放一个棋子,而且尽量摆在下面的方格内,使第一纵行的方格有按条件放棋子的位置。然后如前述,在第三纵行尽可能低的方格放棋子,以后以此类推,力求在该行尽可能低的方格放棋子,目的是使后一纵行有按条件放棋子的位置。当在纵行出现没有按条件放棋子的位置时,应按游戏规定的条件以最少的格数升高前一纵行所摆棋子的位置。如果没有方格升高,就应去掉所有8个棋子,重新按上述升高位置摆第一纵行的棋子,并按前述摆其余各纵行的棋子。必须指出,只有右边没有按条件摆棋子的位置时,才能这样做。
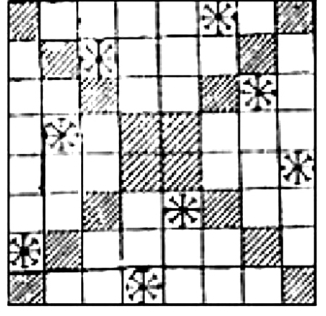
图1—17
这种摆棋子的方法,虽然时间长,但系统,一定能达到游戏的要求。
四步围成圆
共有24个答案。现用数字表示:
(1)1—2,3;2—6,5;6—1,3;1—6,2
(2)1—2,3;4—1,3;3—6,5;5—3,4
(3)1—4,5;3—4,1;4—2,6;2—3,4
(4)1—4,5;5—2,6;6—4,1;1—6,5
(5)2—3,4;3—1,6.5;6—2,4;2—1,6
(6)2—3,4;5—2,3;3—1,6;1—3,5
(7)2—4,5;5—1,3,6;6—2,4;2—1,6
(8)2—4,5;3—2,5;5—1,6;1—5,3
(9)3—1,2;5—3,2;2—2,6;4—5,2
(10)3—1,2;4—3,1;1—6,5;5—1,4
(11)3—1,2;1—2,6,4;6—2,3;3—6,5
(12)3—1,2;2—1,6,5;6—3,1;3—6,4
(13)3—4,5;2—3,5;5—1,6;1—2,5
(14)3—4,5;1—3,4;4—2,6;2—1,4
(15)3—4,5;4—1,6,5;6—5,3;3—2,6
(16)3—4,5;5—2,6,4;6—3,4;3—1,6
(17)4—3,2;3—1,6,5;6—2,4;4—5,6
(18)4—3,2;1—4,3;3—5,6;5—3,1
(19)4—1,2;1—3,6,5;6—2,4;4—6,5
(20)4—1,2;3—1,4;1—6,5;5—1,3
(21)5—3,4;4—1,6;6—3,5;5—6,4
(22)5—3,4;2—3,5;3—1,6;1—2,3
(23)5—1,2;3—2,5;2—6,4;4—3,2
(24)5—1,2;1—4,6;6—2,5;5—1,6
交换棋子的位置
最少的交换次数是19次。
最省的交换法是链式(位置)交换。例如棋子1和7交换后,7和第7方格内占据的那个棋子交换,即和棋子20交换。之后棋子20和第20方格内占据的那个棋子16交换。之后,棋子16和占据在第16方格棋子11交换。以此类推,直到链终了为止。所谓链终,就是两个应交换的棋子按顺序占据在自己的位置上。
链终了时,进行新的交换链,直到链终。
这个游戏必需交换的棋子是5个链:
(1)1和7;7和20;20和16;16和11;11和2;2和24。
(2)3和10;10和23;23和14;14和18;18和5。
(3)4和19;19和9;9和22。
(4)6和12;12和15;15和13;13和25。
如果按所有棋子最初位置依次写成一排,并在它的下面写出顺序数,则能事先确定它们的交换方式:
7、24、10、19、3、12、20、8、22……6
1、2、3、4、5、6、7、8、9……25
删去第一对1和7,确定为第一次的交换数。然后在下面的一排数中找出7上面的数20,删去20和7这一对数,确定为第二次交换。然后在下面的这一排数找到20,它上面的数是16,删去20和16,确定为第三次交换。以此类推。
当链终时,从未删去数最左边开始,进行新的链交换。
在最坏的时候只有一个链,这时要交换的棋子至少要进行25-1=24次交换。最后一次交换,两个棋子占据在它自己的位置上。
图—18
我们的情况是5条链,但有一个棋子(8号棋子)开始就占据在它自己的位置上,所以必须而且最少交换次数应是25-5-1=19。
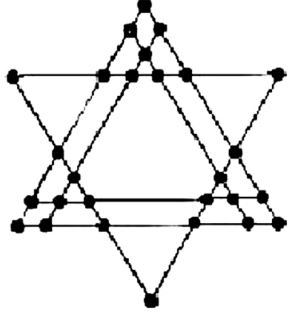
黑白棋子
详见图1—18。白棋子只能往上移动或向上跳,黑棋子只往下移动或往下跳。走的顺序是黑白白黑黑黑白白白黑黑黑白白黑,共15步。
拼成一个圆片
答案详见图1—19。
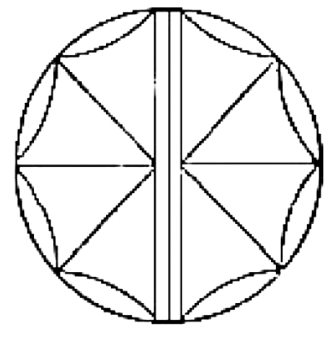
图1—19
一笔把9个圆点连起来
这题的答案并不唯一,图1—20只是答案之一,其他的答案请你来画一画。
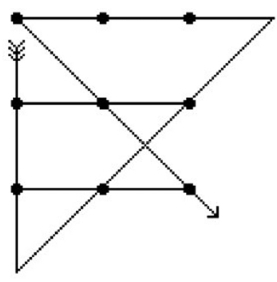
图1—20
按另一种方式栽橡树
详见图1—21。
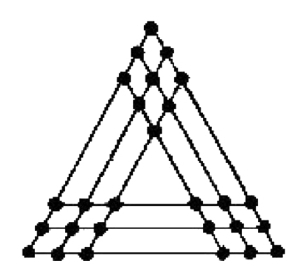
图1—21
栽玫瑰花
详见图1—22。
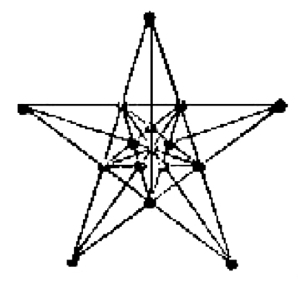
图1—22
一朵八瓣花
详见图1—23。
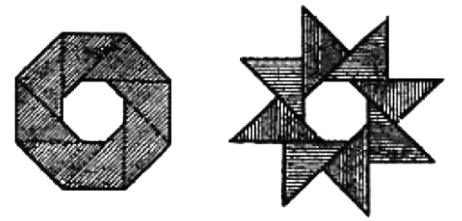
图1—23
用棋子摆方阵
详见图1—24a和b。a方阵在4顶角各放2个棋子。b是用9个棋子摆成方阵。获得了3条垂直线和3条水平线。剩余的3个棋子摆在方阵一对角线上。

图1—24a

图1—24b
确定木材直径
直接测量树节切处从胶合板的一边到另一边的距离,它约为整张胶合板的2/3。
胶合板宽度150厘米,由此可知两切处的距离,或木料这一层的周边为100厘米,故厚木料的直径约32厘米。
纸 虾
详见图1—25a、b。
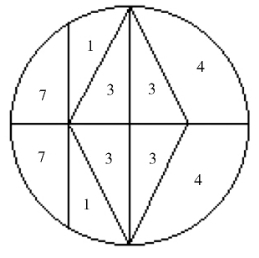
图1—25a
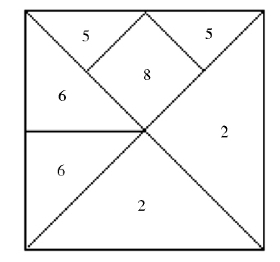
图1—25b
保持面积成比例
详见图1—26。
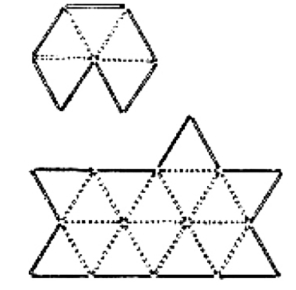
图1—26
篱 笆
详见图1—27。
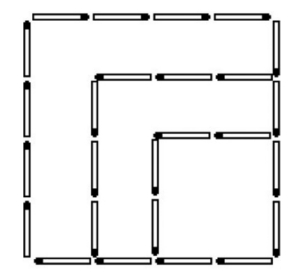
图1—27
数正方形
大大小小的正方形共36个。
向左转
详见图1—28。
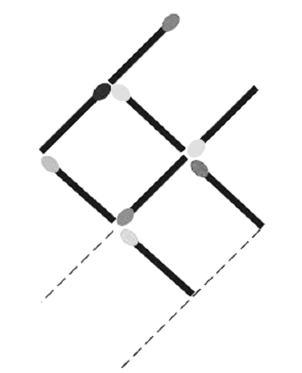
图1—28
做个小建筑师
详见图1—29。
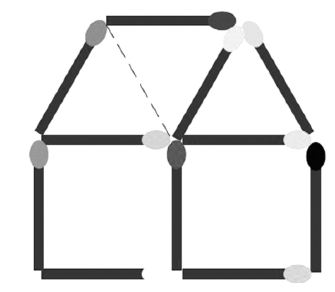
图1—29
奇怪的锁
这把锁的设计在于如果你把钥匙拔出来,锁栓就变成了一条直线,那样你不用钥匙就可以开门了。事实上。只有你把钥匙插进去才能把门锁住。
玻璃钢里的鱼
详见图1—30。
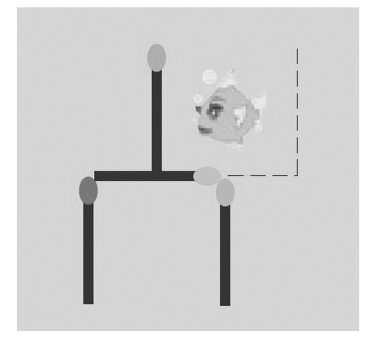
图1—30
单笔画
不能一笔画成的是图—34、图—36、图—38。告诉你一个小窍门,我们能一笔画成的图形,一定时那些没有交叉点或只有两个交叉点的图形,而汇集在这两个交叉点上的直线段或曲线段又必须是奇数的。用这个方法你就能判定哪些图形能一笔画成,而哪些图形不能一笔画成。
本题中能够一笔画成的图形可以按下面的方法来画。
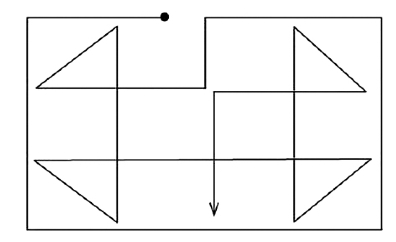
图1—31
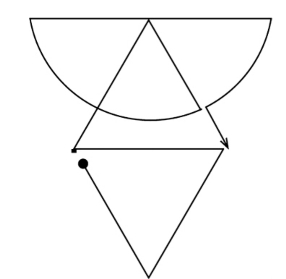
图1—32
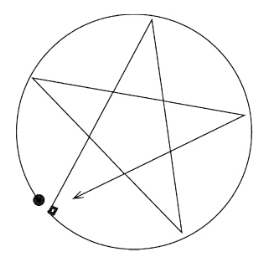
图1—33
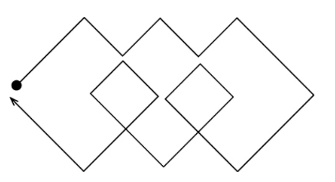
图1—35
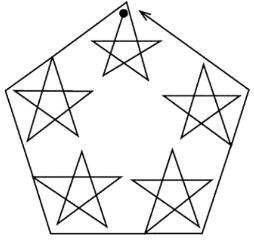
图1—37
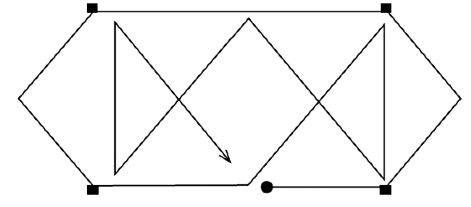
图1—39
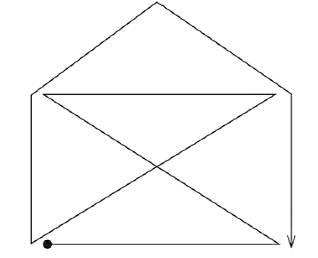
图1—40
处决犯人
求这个问题的通用公式困扰了数学家们几个世纪。而最好的解法是尝试。在36个人中,你应该把你的敌人安排在这些位置:4、10、15、20、26和30。
老实的骗子
如图1—41所示。从爷爷的左边开始。依次是儿子、女儿、爸爸、妈妈。
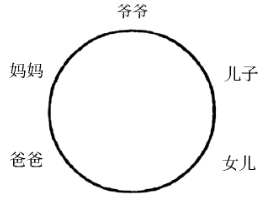
图1—41
谁在前面谁在后面
他们的顺序以此是:戊、丙、己、丁、甲、乙。
多变的三角形
经过观察可以发现,原图中每个三角形的其中两边,都是另两个三角形一边的延长。线能延长,顶点能否连接?这样思维便突破了原图的框架。如果将顶点连接线再继续延长,势必又会出现3个交点,于是这3个交点也就可以成为新三角形的顶点了。
所以答案是可以。如图1—42所示,再加一个大正三角形,大小不一的正三角形就可以有14个了。
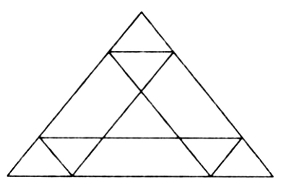
图1—42
火柴游戏
详见图1—43。
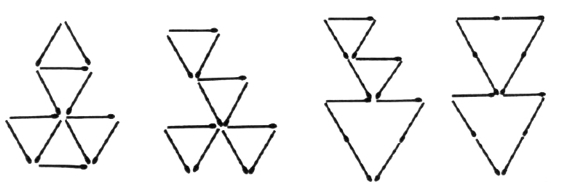
图1—43
快乐七巧板
详见图1—44。
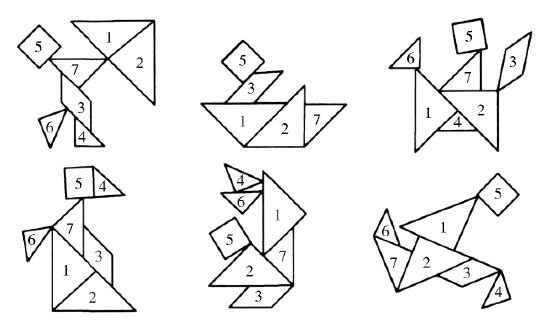
图1—44
杯子游戏
将第二只杯子与第四只杯子里的水分别倒入第七只与第九只空杯子中。
有趣的类比
8。图中的方格被编以1到9之间的号,从左上角开始,先从左到右,再从右到左,最后又从左到占。

图1—45
枪 眼
一块板上能构造出的洞的最大数目不可能超过多米诺骨牌的数量。实际上,如果板的一边长可以被3整除,那么洞的最大数目就是两边长的乘积再除以3。
芭芭拉偷点心
芭芭拉从第8扇门进去,这样能一次吃完所有点心且路线不重复。其路线如图1—46。
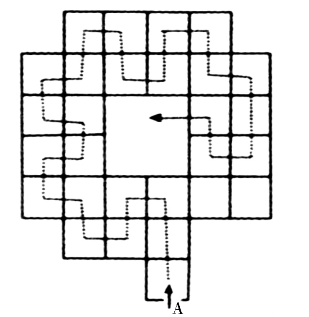
图1—46
“十”字标记
详见图1—47。
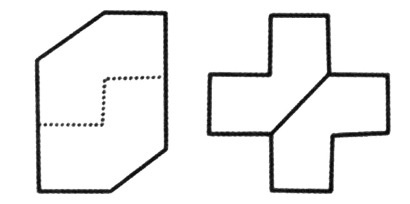
图1—47
一笔画图
这个图可以经过13个转折一笔画成:
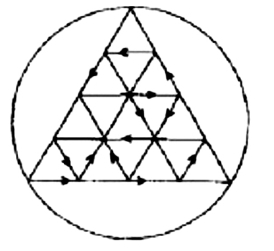
图1—48
变方块
详见图1—49。
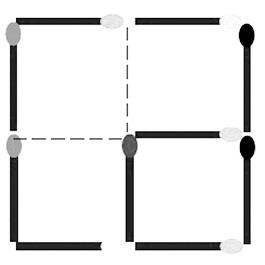
图1—49
