3.概率计算
上面关于扩散的讨论只是把概率的统计定律应用于分子运动的一个简单例子。在深入讨论之前,我们要尽力理解有关熵的所有重要理论,它适用于所有物质的热运动,小到一滴液体,大到由恒星组成的宇宙。我们要先学习一点计算各种简单和复杂事件的可能性(即概率)的方法。
到目前为止,最简单的概率计算问题应该是掷硬币问题。我们都知道,抛出的硬币正面朝上和反面朝上的机会是相等的(如果不作弊的话)。在数学上我们说这种机会是均等的。如果把得正面的机会和得反面的机会相加,就得到![]() 。在概率论中,1 意味着必然发生。在抛掷硬币时,你可以肯定地判断,不是得正面就是得反面,除非硬币滚到沙发下找不到了。
。在概率论中,1 意味着必然发生。在抛掷硬币时,你可以肯定地判断,不是得正面就是得反面,除非硬币滚到沙发下找不到了。
假设你把一枚硬币抛掷2次,或者同时抛掷2 枚硬币(这两种情况是一样的),那么不难看出,会有图84所示的4种可能性。
第一种情形是得到2 个正面,最后一种情形是得到2 个反面,中间的两种情形实际是同一种,因为哪枚是正面,哪枚是反面是无所谓的。这样,我们可以说,得到2 个正面的机会是1∶4,即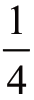 ;得到2 个反面的机会是1∶4,即
;得到2 个反面的机会是1∶4,即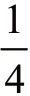 ;得到一个正面一个反面的机会是2∶4,即
;得到一个正面一个反面的机会是2∶4,即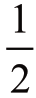 ;因此可以得到
;因此可以得到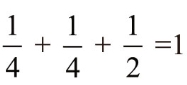 。这就是说,抛掷2 枚硬币,三种情形必定会出现一种。再来看抛掷3 枚硬币的情形,可能性概括起来如下:
。这就是说,抛掷2 枚硬币,三种情形必定会出现一种。再来看抛掷3 枚硬币的情形,可能性概括起来如下:

图84 抛掷2次硬币的4 种可能组合
第一枚 正 正 正 正 反 反 反 反
第二枚 正 正 反 反 正 正 反 反
第三枚 正 反 正 反 正 反 正 反
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ
可以看出,三枚硬币均为正面的概率为 ,三枚硬币均为反面的概率也为
,三枚硬币均为反面的概率也为 ,剩余的两正一反和两反一正的概率相等,均为
,剩余的两正一反和两反一正的概率相等,均为 。
。
我们再看看抛掷4 枚硬币的情形。这时有以下16 种可能性:
第一枚 正 正 正 正 正 正 正 正 反 反 反 反 反 反 反 反
第二枚 正 正 正 正 反 反 反 反 正 正 正 正 反 反 反 反
第三枚 正 正 反 反 正 正 反 反 正 正 反 反 正 正 反 反
第四枚 正 反 正 反 正 反 正 反 正 反 正 反 正 反 正 反
Ⅰ Ⅱ Ⅱ Ⅲ Ⅱ Ⅲ Ⅲ Ⅳ Ⅱ Ⅲ Ⅲ Ⅳ Ⅲ Ⅳ Ⅳ Ⅴ
因此,我们得到4 个正面的概率为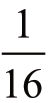 ,得到4 个反面的概率也为
,得到4 个反面的概率也为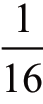 ,三正一反和三反一正都各有
,三正一反和三反一正都各有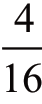 即
即 的概率,正反相等的概率为
的概率,正反相等的概率为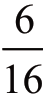 ,即
,即 。
。
如果你试图用相同的方式抛掷硬币许多次,这个表格就会非常长,很快你的纸上就会写不下。例如,抛掷10次会得到1 024种可能性(即2×2×2×2×2×2×2×2×2×2)。不过,我们根本不必要罗列这么长的表格,只要从前面列过的几张简单情况的表格中,就可以观察出判断概率大小的简单法则,并把它运用到较复杂的情况中去。
首先,我们可以看到,抛掷两次得到2 个正面的概率等于第一次和第二次分别得到正面的概率的乘积,具体说来就是
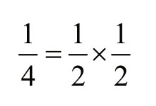
同样,连得3 个正面和连得4 个正面的概率也为每次抛掷得正面的概率的乘积:
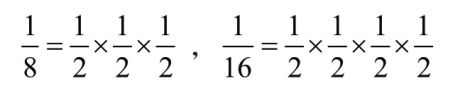
如果有人问连掷10次均得正面的概率有多大,你可以毫不费力地把10 个 相乘的结果告诉他,这个数是0.000 98。它表明出现这种情况的可能性很小,大概只有千分之一的机会!这就是概率乘法法则。具体地说,如果你需要同时得到几个不同的时间的概率,你可以把单独一个时间发生的概率相乘得到总的概率。如果你有许多事件,每一个事件实现的概率都很低,那么,你希望它们全部实现的概率实在是低得令人沮丧。
相乘的结果告诉他,这个数是0.000 98。它表明出现这种情况的可能性很小,大概只有千分之一的机会!这就是概率乘法法则。具体地说,如果你需要同时得到几个不同的时间的概率,你可以把单独一个时间发生的概率相乘得到总的概率。如果你有许多事件,每一个事件实现的概率都很低,那么,你希望它们全部实现的概率实在是低得令人沮丧。
另外,还有一个法则,那就是概率的加法法则。内容是:如果你需要事件中的一个(任意一个都行),这个概率就等于所需的各个事件单独实现的概率之和。
概率的加法法则可以用将一枚硬币抛掷2次,得到正反各一的概率相等的例子来说明。你所需要的“先正后反”或者“先反后正”这两个事件,每个单独实现的概率均为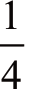 ,因此“先正后反”或者“先反后正”事件发生的概率为
,因此“先正后反”或者“先反后正”事件发生的概率为![]() 。总之,如果你要求的是“某事,和某事,还有某事……”同时发生的概率,就应该把各事单独实现的概率相乘;如果是求“或者某事,或者某事,或者某事……”的概率,就应该把各个概率相加。
。总之,如果你要求的是“某事,和某事,还有某事……”同时发生的概率,就应该把各事单独实现的概率相乘;如果是求“或者某事,或者某事,或者某事……”的概率,就应该把各个概率相加。
第一种情况,所有事件都发生的概率,要求的事件越多,实现的可能性越小;第二种情况,即只求某一事件发生的情况,供选择的事件越多,得到满足的可能性越大。
当实验的次数很多时,概率定律就变得很精确了。抛掷硬币的实验很好地证明了这一点。图85 给出了抛掷2次、3次、4次、10次和100次硬币时,得到不同正、反面分布的概率。可以看出,抛掷的次数越多,概率曲线就变得越陡峭,正、反面均以0.5 的概率出现的峰值也就越突出。
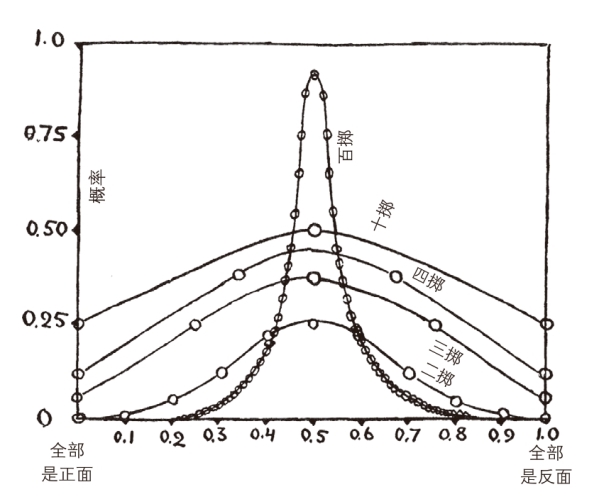
图85 得到正面、反面的相对次数
因此,在投掷2次、3次以至4次的情况下,出现全是正面或全是反面的概率是可计算的。在投掷10次的情况下,出现90%是正面或反面的概率也是很低的。如果次数更多,例如投掷100次或1 000次,概率曲线会变得像一根针,即使在对半的分布上稍微偏离一点点,实际上也是不可能实现的。
现在,我们用刚刚学过的概率计算的简单法则,判断在一种有名的扑克游戏中,5 张牌出现各种组合的可能性。
如果你还不会玩这种扑克游戏,我先简单介绍一下规则:参加者每人摸5 张牌,得到最好的组合牌型者为赢家。这里我们忽略为了凑成一手好牌而交换几张牌所引起的附加变化,也不讨论用诈术给对方造成你得到好牌的错觉而自动认输的心理学战术——其实诈术才是这种牌的核心所在,并使丹麦著名物理学家玻尔设计了全新的玩法:根本无须用牌,参加者只需要说出自己想象的组合,并相互蒙诈就行。这已全然超出概率计算的范畴,成了纯心理学的问题。
现在让我们以计算出现某些组合的概率作为练习。有一种组合叫作“同花”,即5 张牌都属于同一花色(见图86)。

图86 同花(黑桃)
如果想要摸到一副同花,第一张牌是什么无所谓,只要计算另外4 张和第一张属于同一个花色的概率就行了。一副牌共52张,每一种花色有13 张[7],在你摸去第一张以后,这种花色只剩下12 张。因此,第2 张也属于这一花色的机会为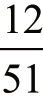 。同样,第三、第四、第五张属于同一花色的概率分别为
。同样,第三、第四、第五张属于同一花色的概率分别为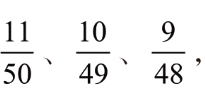 既然我们求5 张牌为同一花色的概率,就要用概率的乘法法则。这样,你会发现,得到同花的概率为:
既然我们求5 张牌为同一花色的概率,就要用概率的乘法法则。这样,你会发现,得到同花的概率为:
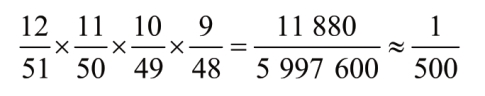
但是,不要以为每摸500次,一定会得到一次同花,你可能一次也摸不到,也可能摸到两次,我们这里仅仅是在计算可能性。有可能你连摸500 多次,一次同花也摸不到;也可能恰恰相反,你第一次就摸到同花。概率论所能告诉你的,只是在500次游戏中,可能碰到一次同花。用同样的方法可以计算出,在三千万次游戏中,可能有10次得到5 张“爱司”(包括一张“百搭”在内)的机会。
另一种更为少见,因而也就有更为宝贵的组合就是所谓的“福尔豪斯”,又称为“三头两只”。它包括一个“对”和一个“对半”(即有2 张牌同一点数,另外的3 张牌为相同的另一点数,如图87 所示的2 张5、3 张Q)。

图87 三头两只
做成“三头两只”时,前两张牌为什么点数是无所谓的,但在后面的3 张牌中,则应有两张与前面的两张之一的点数相同,第三张与前面两张中的另一张点数相同。因为除了前两张牌,还剩下六张牌(如果已摸到1 张5、1 张Q,那就还剩下3张5 和3 张Q)可供组合,所以第三张满足要求的概率是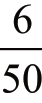 ;在剩余的49 张牌中还有5 张合格的牌,所以第四张也满足条件的概率为
;在剩余的49 张牌中还有5 张合格的牌,所以第四张也满足条件的概率为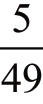 ;第五张也满足要求的概率为
;第五张也满足要求的概率为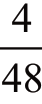 。因此,得到“三头两只”的概率为:
。因此,得到“三头两只”的概率为:
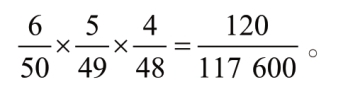
数值大约是同花概率的一半[8]。
同样,我们还能计算出其他组合如“顺子”(即点数连续的五张牌)等的概率,以及算出包括“百搭”在内和进行交换所表现的概率来。
通过计算可以看出,扑克中一副牌的好坏正是与它的数学概率值相对应的。这究竟是以前的某位数学家整理提出的,还是靠聚集在全世界的各个豪华或破烂赌窟里数以百万计的赌徒们用钱财冒险总结经验得来的?我们不得而知。如果是后者,我们必须承认对于复杂事件的相对概率来说,我们有一个相当好的统计素材。
另一个有趣而结果出乎意料的概率计算的例子是所谓的“生日重合”问题。回忆一下,你是否在同一天被邀请参加两个不同的生日聚会。你可能会说这种可能性很小,因为你大概只有24位朋友会邀请你参加他们的生日聚会。而一年有365 天,既然有这么多的天数可供选择,因此,你的24 个朋友中,两个人在同一天吃生日蛋糕的机会一定是非常小的吧!
然而,你的判断大错特错。尽管听起来似乎不能令人置信,但实际情况却是:24 人中,有两个人、甚至几组两个人生日相重合的概率是相当高的,实际上要比不出现重合的概率还要大。
你可以通过列出24 人的生日表来证明这一点或者直接从《美国名人录》之类的书中任选一项,随意点出24 个人来查查看。当然,我们也可以用在投掷硬币和玩扑克这两个例子中的简单概率运算法则,来计算这道题目的概率。
我们先来计算24 个人生日各不相同的概率,先看第一个人,她的生日可以是365 天中的任意一天。那么,第二个人与第一个人生日不在同一天的概率有多大呢?第二个人可能出生在一年中的任何一天,他有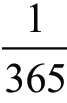 的概率与第一个人重合,当然有
的概率与第一个人重合,当然有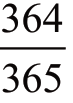 的概率不重合。同样,第三个人与前面两人都不在同一天出生的概率为
的概率不重合。同样,第三个人与前面两人都不在同一天出生的概率为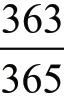 ,这是排除前两天的缘故。再后面的人,生日不与前面任何一个人生日相同的概率依次为
,这是排除前两天的缘故。再后面的人,生日不与前面任何一个人生日相同的概率依次为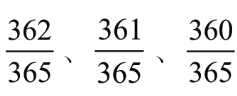 ,等等。最后一个人的概率为
,等等。最后一个人的概率为
把所有这些分数相乘,得到所有人的生日都不相重合的概率为:
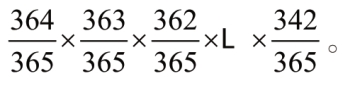
用高等数学的方法进行计算,几分钟就可以得出乘积来。如果不用高等数学,那只能用直接相乘的办法一步一步算出来,这费不了多长时间。结果约为0.46,这说明生日不相重合的概率稍小于0.5。换句话说在这24 个朋友中,没有两个人在同一天过生日的可能性为46%,而有重合的可能性是54%。所以,你有25个朋友或更多些,但却从来没有在同一天被两个人邀请去赴生日聚会,那么你可以做出肯定的判断,要么他们大多数人不搞生日聚会,要么他们没有邀请你参加。
这个生日重合的问题可以作为一个很好的例子,来说明通过常识想当然地来判断复杂事件的概率是多么不靠谱。我本人曾问过好多人这个问题,其中还有不少是卓越的科学家,结果除一人外,其他人都下了从2 对1 到15 对1 的赌注打赌说,不会发生这种可能性。如果某个人跟他们都打了赌,他一定可以靠此发财。
有一点需要再次强调,尽管我们能够依据给定你的规则把不同事物发生的概率计算出来,并找出其中最大的概率,但这并不等于我们能够确定接下来会发生什么。除非我们把试验重复做上千遍、上万遍,重复上亿遍更好,否则我们只能推测说“大概”会怎么样,而不能说“一定”会怎么样。当只进行有限的几次试验时,概率定律就不那么管用了。我们来看一个试图用统计规律来翻译一段密码的例子。在爱伦·坡(Edgar Allan Poe)的著名小说《金甲虫》中,有一位勒格让先生,当他在南卡罗来纳州的荒凉的沙滩上溜达时,发现了一张半埋在湿沙里的羊皮纸。当在寒冷的室外时,羊皮纸上什么也没有,但在勒格让先生的房间里受了火炉的烘烤后,就显现了一些清晰可辨的神秘的红色字符。符号里有一个骷髅头,暗示着这份手稿是一个海盗所写;还有一个山羊头,说明这个海盗正是有名的基德船长;还有一些符号,无疑是指明一处埋藏珍宝的地方(见图88)。

图88 基德船长的手稿
我们不妨尊重爱伦·坡的威望,姑且承认17 世纪的海盗认识分号、引号和今天常用的各种符号,如![]() 等。
等。
为了得到那笔钱,勒格让先生绞尽脑汁想译出这段密码,最后,他按照英文中各个字母出现的相对频率来进行破译。他的依据在于:随便找一段英文,不管是莎士比亚的十四行诗还是华莱士的侦探小说,统计各个字母出现的频率,就会发现字母e 出现的频率遥遥领先,其余字母出现频率的顺序依次是:
a,o,i,d,h,n,r,s,t,u,y,c,f,g,l,m,w,b,k,p,q,x,z。
勒格让数了数基德船长的密码,查出数字8 出现的次数最多。“啊哈,”他想,“也就是说,8 大概是e。”
是的,在这一点上他猜对了。当然,这只是大概,而不是一定。如果这段密码写的是“You will find a lot of gold and coins in iron box in woods two thousand yards south from an old hut on Bird Island′s north tip(在鸟岛北端的旧茅屋南面2 000 码处树林中的一个铁箱内,你可以找到许多金币)”,这里可就一个e 也没有!不过概率论帮了勒格让的大忙,他真的猜对了。
第一步走对了,这使得勒格让先生信心大增,他按同样的方法列出了各字母出现的次数表。表4 就是按出现频率排列的基德船长手稿中的符号表。
表4 基德船长手稿中的符号表
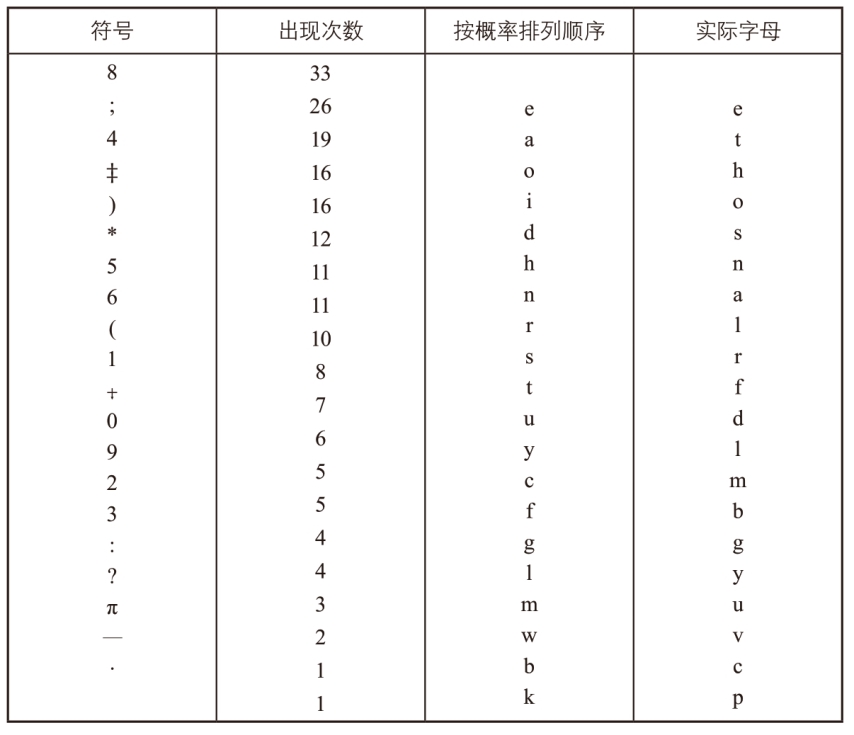
表中第三列是按各字母在英语中出现的频率排列的(由高到低),所以有理由假设第一栏中的各符号与同一行中的字母逐个对应。但是按照这样的安排,基德船长的手稿开始的部分就变成了ngiiugynddrhaoefr…
这串字母什么意思也没有!
怎么回事呢?是不是基德这个老海盗诡计多端,采用了与英语字母出现频率不相同的另一套特别的单词呢?不可能。原因很简单,这篇文字太短了,以致概率学的最大概率分布不起作用。如果基德船长把珍宝以一种很复杂的方法藏起来,然后用好几页纸写成密码,那么勒格让先生用概率论来解释这个谜就会有把握得多;如果是一本厚厚的书,那就更不成问题了。
如果抛掷硬币100次,你可以很有把握地判断正面朝上的次数约为50次,但是抛掷4次,你可能得到3次正面朝上、一次反面朝上或者3次反面朝上、一次正面朝上。试验次数越多,概率计算就越精确,这时它才能成为一条定律。
由于这篇密码的字数太少,不足以运用统计分析,勒格让先生只能凭借英语中单词的细微字母结构来进行破译。首先他依然假设出现次数最多的“8”为字母“e”,因为他注意到“8 8”组合在这小段文字中经常出现(5次)。大家知道,e 在英语中是经常双写的,如meet、fleet、speed、seen、been、agree 等。其次,如果“8”真的是e,那么它一定为作为“the”的一部分在文中经常出现。查阅手稿,我们发现“;48”这个组合在文中出现了7次,因此我们假设“;”为t,“4”为h。
读者们可以自己去破译爱伦·坡这篇故事中基德船长的秘密文字。原文如下:“A good glass in the bishop′s hostel in the devil′s seat.Forty-one degrees and thirteen minutes northeast by north.Main branch seventh limb east side.Shoot from the eye of the death′s head.A beeline from the tree through the shot fifty feet out.(主教驿站内的魔像座位下面有面镜子。北偏东41°13′。主干上朝东的第七根树枝。向骷髅的眼睛开一枪。从那棵树沿子弹方向走50 英尺)”。
勒格让先生最后译出的字母列在表上最后一栏,可以看出,它们与概率定律统计的字母分布不甚相符。不过,在这个小小的统计样品中,我们也能注意到各个字母有按概率论的要求排列的趋势,一旦字母的数量足够大,这个趋势就会变成确凿的事实。
关于用大量试验来实际检验概率论的例子大概只有一个,这就是著名的星条旗与火柴的例子(排除保险公司不会破产的事实)。
为了验证这个特殊的概率问题,你需要一面美国国旗,即那种红白条相间的旗子。如果没有这种旗子,在一张纸上画上若干道等距的平行线即可。然后再拿一盒火柴——什么火柴都行,确保它们短于平行线间的距离即可。此外,还需要一个希腊字母π。它除了是一个希腊字母,还表示圆的周长与直径的比值。你可能知道这个数值,大约等于3.141 592 653 5…(还有许多位数字,不过没必要再继续写下去)。
现在把旗子铺在桌子上,投掷一把火柴,然后看它们落在旗子上(见图89)。它们可能完全落在一条带子上,也可能全部压在两条带子上。这两种情况发生的概率各有多大呢?
要想确定概率,首先也得像其他题目一样,弄清各种可能情况发生的次数各为多少。
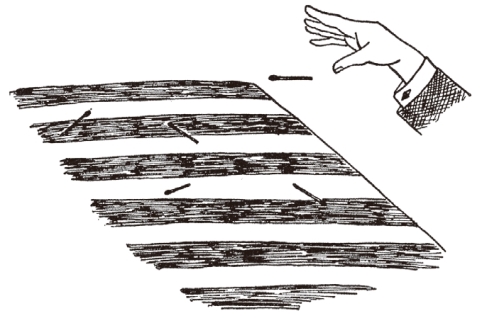
图89 在旗子上投掷火柴
但是,火柴落在旗子上有无限多种方式,怎么能确定所有的可能性呢?
让我们把这个问题仔细考虑一下。火柴落在条带上的情况,可由火柴中心点到最近条带边界的距离以及火柴与条带走向所成的角度来决定。如图90 所示,我们给出三种典型的火柴落在条带上的情况。为简便起见,把火柴的长度与条带宽度取相同的值,2 英寸。如果火柴的中点离边界很近,角度又较大(如例a),火柴便与边界相交。相反地,如果角度较小(如例b),或者距离较大(如例c),火柴就会全部落在一条条带上。更精确地说,如果火柴长度的一半在竖直方向上的投影大于从火柴中点到最近边界的距离,则火柴与边界相交(如a),反之则不相交(如b 和c)。这句话可用图90 下半部分的图形表示出来:横轴以弧度为单位,表示火柴落下的角度;纵轴是火柴的半长径在竖直方向的投影长度,在三角学中,这个长度叫作给定角度的正弦。显然,当角度为零时,正弦值也为零,这种情况时火柴呈水平状态。当角度为 即直角[9]时,火柴处于竖直位置,与其投影重合,正弦值为1。对于处于两者之间的情况,其值由大家熟悉的正弦曲线给出。
即直角[9]时,火柴处于竖直位置,与其投影重合,正弦值为1。对于处于两者之间的情况,其值由大家熟悉的正弦曲线给出。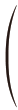 图90 只画出了从0 到
图90 只画出了从0 到 这四分之一段的曲线。
这四分之一段的曲线。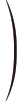
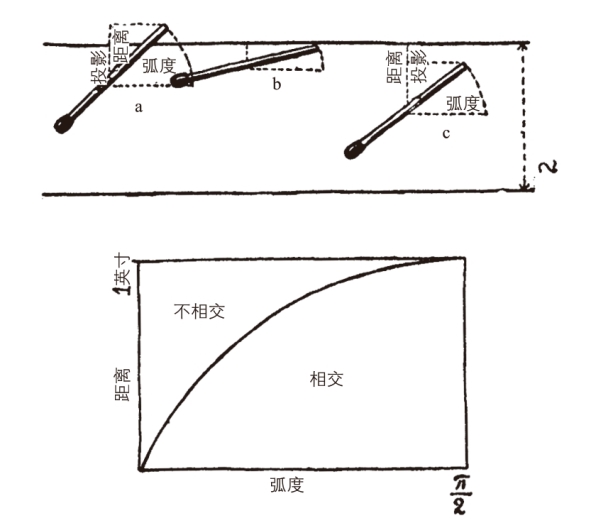
图90 三种典型的火柴落在条带上的情况
有了这条曲线,我们可以方便地计算出火柴与边界相交或不相交这两种情况的概率。实际上,正如前文我们所看到的(再看图90 上部的三个例子),火柴中点离边界的距离如果小于半根火柴的竖直投影,即小于此时的正弦值,火柴就会与边界相交。这时,代表这个距离和角度的点在正弦曲线以下。与此相反,火柴完全落在一个条带内时,相应的点在曲线之上。
按照概率计算的规则,相交的机会与不相交的机会的比值等于曲线下方的面积与曲线上方的面积的比值。也就是说,这两个事件的概率,各等于自己那一块的面积除以整个矩形的面积。可以由数学方法(第二章)证明,图中正弦曲线下方的面积为1,整个矩形的面积等于![]() 。所以我们得出结论:火柴(在长度与条带宽度相等时)与边界相交的概率为
。所以我们得出结论:火柴(在长度与条带宽度相等时)与边界相交的概率为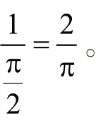
π 在这个最意想不到的场合跳了出来,这件有趣的事实是18 世纪的科学家布丰(George Louis Leclerc Buffon)最先注意到的,因此这个问题也被称作布丰问题。
具体的实验是由一位勤奋的意大利数学家拉兹瑞尼(Lazzerini)进行的,他一共抛掷了3 408 根火柴,发现有2 169根火柴与边界相交。以这个真实数据代入布丰公式,得到π 的值为3.141 592 9,与π 的精确数值相比,一直到第七位小数才不相同。
这个例子对于概率定律的适用性无疑是一个有趣的证明。但比起抛掷几千次硬币,用投掷总数除以正面朝上的总数可得2 这个结果来,却也有趣不到哪里去。在后一种场合,你一定会得到2.000 000…,误差也会和拉兹瑞尼所确定的π 值的误差一样小。
