基本思想与应用：鲍威尔法共轭方向优化

采用最优步长的坐标轮换法，对于计算一个非线性函数的极小值，其收敛速度有时是相当慢的。但是，如图4-9所示，若把前一轮搜索末点向量X₁^（2）（或X₂^（1））和这一轮搜索末点向量X₁^（2）（或X₂^（1））用向量S相连，则其方向将直指椭圆等值线族的中心。利用这个方向进行搜索，显然可加快收敛速度。由前面的“共轭梯度法”中知，向量S和S₁是关于正定矩阵A共轭的，其中S和S₁的方向为共轭方向。利用共轭方向作为搜索方向尽管可行，但如何确定每次的迭代方向，尤其对高维问题，用鲍威尔（Powell）提出的方法可较好地获得解决。

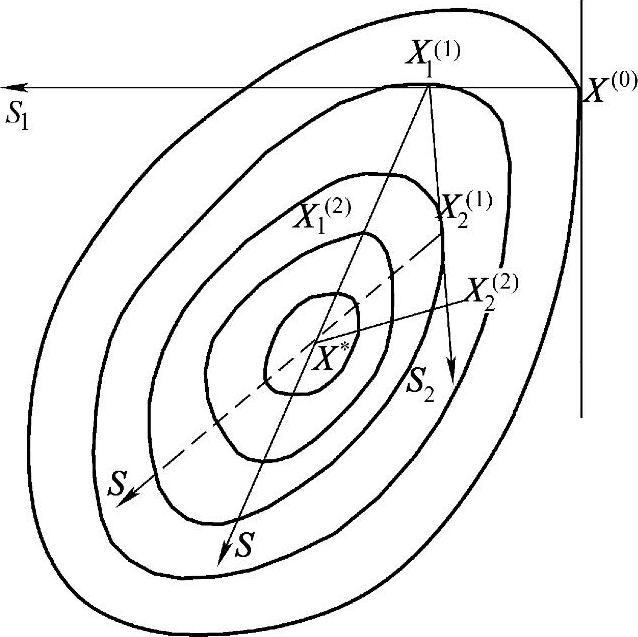
图4-9 共轭方向图解

鲍威尔法是一种改进的共轭方向法，它不需要对目标函数作求导计算。用于变量10＜n≤20或目标函数的一阶导数不连续的最优化问题时，亦能得到很好的结果。在机械优化设计中，常使用鲍威尔法配合惩罚函数法来处理约束最优化问题。

如图4-10所示的二维正定二次函数：

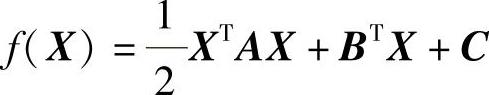
X=[X₁，X₂]^T

根据极值条件，有

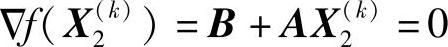
和(https://www.daowen.com)

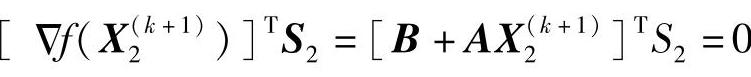
两式相减得

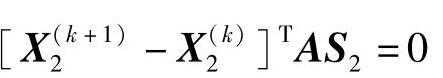
令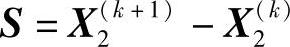，得

S^TAS₂=0 （4-26）

即构造的方向S和两平行向量S₂是关于A共轭的。按照同心椭圆族的几何特性，即是两条平行的任意方向切线，其切点的连线必通过椭圆族的共同中心（图4-10）。

利用共轭方向的性质去逐次构造方向，并以此为搜索方向形成的算法就是共轭方向法。通常，对于二维二次正定函数，使用两个共轭方向就可达到极小点；而对n维二次正定函数，则使用n个共轭方向即可达到最小点。但是n个共轭方向有可能近似或趋于线性相关，若出现这种情况，则在以后各步搜索将在维数下降了的空间内进行，从而导致计算不能收敛而失败。鉴此，鲍威尔于2025年提出了修正的共轭方向法即鲍威尔法。即在形成新的方向组时，不一定去掉方向S₁^（k），而是有选择地去掉某一方向S^（k）_m+1（1≤m≤n），以避免线性相关。

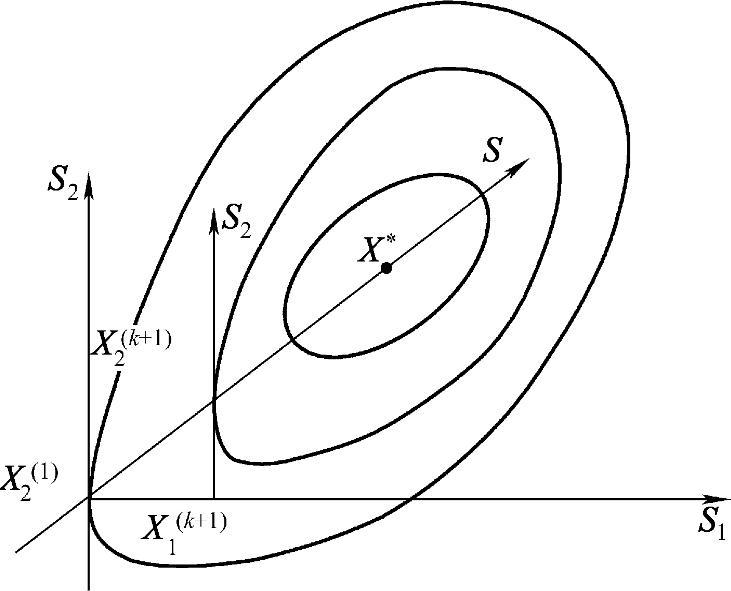
图4-10 二维二次正定函数的共轭方向