热平衡点缺陷的统计学理论分析

在4.1.1节，我们提到，晶体中总是有一定量的缺陷存在。现在我们从热力学角度分析体系为什么有少量缺陷才是稳定的。

1.热力学依据

在一定温度下，一个原子可能会离开正常点阵位置，产生空位。如果这个原子离空位较近，则又可很快回到原来的空位上产生复合。这样就不会有缺陷产生。然而有一些原子能量较高，可以离空位较远，不会很快复合而保持很长时间。同时新的热缺陷还在不断出现，已有热缺陷也在消失。单位时间内产生和消失的热缺陷数目相同时，达到动态平衡。为什么这些热缺陷不会全部消失呢？

根据点缺陷统计理论，我们可将晶体点缺陷的形成看成是等温、等容过程。在其他非体积功W′=0、组成不变的情况下，体系要自发朝自由能降低的方向移动，必须满足亥姆霍尔兹（Helmholtz）自由能ΔA≤0，即ΔA=ΔU-TΔS≤0。若体积变化不能忽略，则由吉布斯（Gibbs）自由能作判据，使ΔG=ΔH-TΔS≤0（适用条件为等温、等压，其他非体积功W′=0，组成不变）。

产生热缺陷，要么需要断键，要么这些缺陷周围有畸变现象（图4.1）。这会引起体系内能U或焓H增加，即ΔU＞0或ΔH＞0。根据熵判据，在封闭体系中，自发变化总是朝熵增加的方向发生。与理想晶格相比，产生缺陷，增大了晶体中原子的无序度。系统原子重新布局，构型熵增加，即ΔS＞0。以上两方面的综合结果，决定了整个晶体体系以什么结构稳定存在。

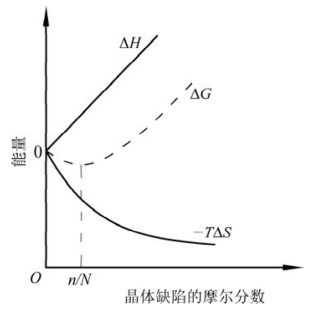
图4.2　体系的ΔS、ΔH、ΔG与缺陷摩尔分数n/N的关系（缺陷数目为n，晶体原子数为N）（引自刘培生，2010）

当缺陷很少，特别是理想晶体产生微量缺陷时，与ΔU、ΔH相比，熵的增量很大，即ΔS值较大。这就导致ΔA=ΔU-TΔS≤0或ΔG=ΔH-TΔS≤0，体系自由能降低而处于稳定态。但随着缺陷量的增多，ΔU、ΔH之值逐渐大于ΔS，体系能量反而增加，使得ΔA、ΔG开始大于0，体系变得不稳定。图4.2表示了在一定温度下，晶体体系的Gibbs自由能与缺陷摩尔分数的关系。在体系自由能ΔG的最低处，缺陷摩尔分数达成动态平衡，此时的缺陷数目n为平衡数目。可见，少量的缺陷可维持体系自由能最低，而无缺陷和过多的缺陷都会使系统能量升高。比如，纳米材料，其缺陷远超过缺陷物理和缺陷化学的研究范畴。这些缺陷使得纳米材料很不稳定，容易团聚在一起以降低能量。但也正是它的缺陷很多，表现出与常规材料不同的性能而引起人们的关注。

根据以上分析，我们可知，无缺陷的晶体材料很难获得，或者说没有无缺陷的实际材料存在。

2.热缺陷的形成及种类

（1）弗仑克尔缺陷

弗仑克尔缺陷是因温度高于0K而形成的点缺陷。在离子晶体中，人们常认为半径大的阴离子作密堆，半径小的阳离子填充在堆积形成的空隙中。因此，是否能形成弗仑克尔缺陷，与结构中的空隙和离子之相对大小有关。比如NaCl型的MgO，其中较大的八面体空隙全部被填满，只剩下较小的四面体空隙。较大的O2-进入间隙位需要的能量高，因此，较难形成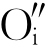。但对于CaF2结构，较大的八面体空隙全空，F-较小，故可形成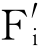和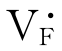。因而CaF2结构比NaCl结构更易形成弗仑克尔缺陷。弗仑克尔缺陷的间隙、空位是成对出现的，故空位和间隙原子数目相等。

离子晶体的弗仑克尔缺陷为离子空位和间隙离子，如MgO晶体中的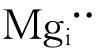和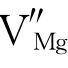。图4.3（a）表示离子晶体中弗仑克尔缺陷的形成。金属单质晶体中的弗仑克尔缺陷为金属原子空位和在间隙位的金属原子，如图4.4（a）所示。有时，晶体表面的原子由于热运动也可进入邻近的间隙位，并在晶体中保持下来。这种间隙原子缺陷也属于弗仑克尔缺陷，如图4.4（c）所示。

（2）肖特基缺陷

原子脱离晶格后，不留在晶体点阵间的间隙位，而是迁移到表面的正常点阵位置，构成新的表面原子层，并在晶体内部阵点处留下空位，如图4.3（b）所示。这种因温度原因引起的空位称为肖特基缺陷。在一定温度下，内部空位与表面原子（离子）达成动态平衡。此外，晶体阵点上的原子还可迁移到位错或晶界处。

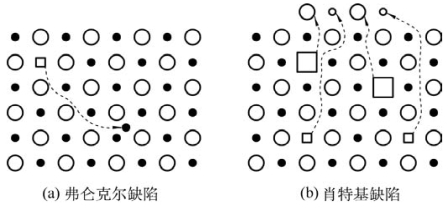
图4.3　离子晶体的弗仑克尔缺陷和肖特基缺陷示意图（空心球表示大半径离子；实心球表示小半径离子；大、小方框分别代表它们的空位）（引自Kingery，2010）

对于离子晶体，由于局部电中性的要求，肖特基缺陷为等电量的正、负离子空位。比如，NaCl晶体，肖特基缺陷为一个钠离子空位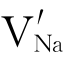和一个氯离子空位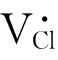。而Al2O3晶体中的肖特基缺陷为两个铝离子空位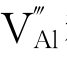和三个氧离子空位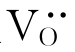。金属晶体中的肖特基缺陷为金属原子的空位，如图4.4（b）所示。

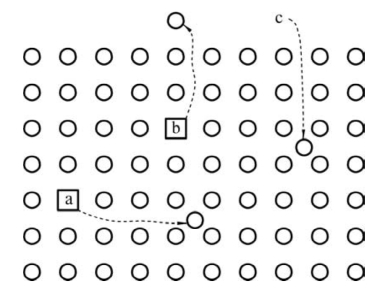
图4.4　金属单质的弗仑克尔缺陷和肖特基缺陷示意图（a为弗仑克尔缺陷；b为肖特基缺陷；c为只有间隙原子的弗仑克尔缺陷；方框代表空位）

综上所述，基本热缺陷有两大类：弗仑克尔缺陷为“空位+间隙原子”，或只有间隙原子；肖特基缺陷为“空位”。实际上，这两种缺陷可能同时存在于一个晶体中。而且，其中的空位还可通过迁移而形成两个或多个空位结合在一起的双空位或空位团。

3.热缺陷的平衡摩尔分数

在热平衡条件下，热缺陷的多少与温度有关，故可用热力学自由能的最小原理计算热缺陷的平衡摩尔分数。假设各点缺陷之间无相互作用，且点缺陷对点阵振动频率无影响；热缺陷数目n≪晶体原子数N。在等温、等压过程中，热缺陷的产生引起的Gibbs自由能变化为ΔG=ΔH-TΔS。如图4.2所示，对ΔG求导，获得极值并求出平衡时热缺陷数目与晶体原子数之比n/N，即平衡摩尔分数。

1）弗仑克尔缺陷

（1）先求ΔG=ΔH-TΔS中的熵增ΔS。由于缺陷很少，我们从微观状态来求ΔS。其中，熵S可由Boltzmann熵定理求得

其中kB为Boltzmann常数；W为粒子总的组合方式数，在统计热力学中称为总微态数。

设某一单质晶体有N个相同原子，N′个间隙位，有n个原子脱离正常点阵进入间隙位n≪N′。在这N个点阵位置中，产生n个空位的组合方式有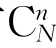种，即

n个原子在N′个间隙位的组合方式有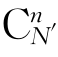种，即

综合空位和间隙原子各自的组合，总的组合方式数，即总微态数有W=W′W″种，即

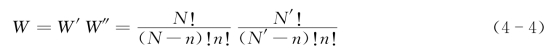
产生n个间隙位、n个空位后的晶体，相对于理想晶体，其熵的增量为

S为产生n个间隙位、n个空位后晶体的熵；S0为理想晶体的熵。对于特定的某种晶型，其理想结构中的原子只有一种排布方式，即W=1。根据式（4-1），S0=kBln 1=0。故ΔS=S-0=S，即

将式（4-4）代入式（4-6）得

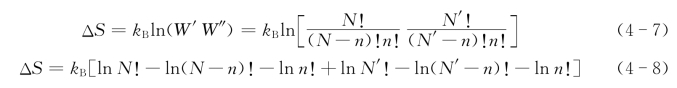
根据Stirling公式lnx！≈xlnx-x，改写式（4-8）并整理得

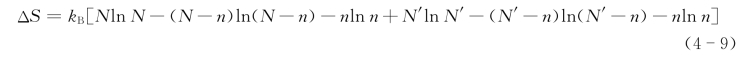
（2）接着求ΔG=ΔH-TΔS中的ΔH

设把一个原子从正常点阵位置移到较远间隙位置，产生一个弗仑克尔缺陷所做的功为hF（含同时产生一个间隙原子所需能量，也就是形成能），则产生n个弗仑克尔缺陷的焓变为

将式（4-9）和式（4-10）代入ΔG=ΔH-TΔS，晶体的吉布斯自由能增量为

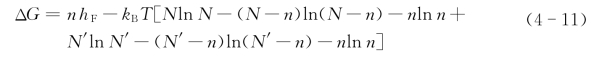
则在一定温度下，对式（4-11）中的ΔG求导，∂ΔG/∂n=0获得极值，整理后得

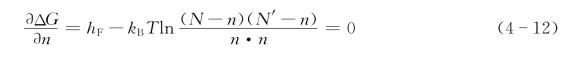
即

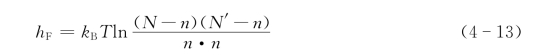
因为缺陷很少，且n≪N，n≪N′，所以N-n≈N，N′-n≈N′，上式变为

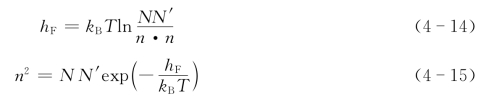
两边同除以N2，得

(https://www.daowen.com)

再开方，得

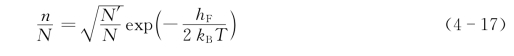
这就是单质晶体（如纯金属）在一定温度下产生n个弗仑克尔缺陷的平衡摩尔分数。

对于二元以上的晶体，如离子晶体，其中的每种离子都可形成弗仑克尔缺陷，且平衡摩尔分数也符合式（4-17）。但相对而言，哪种离子的弗仑克尔缺陷形成能hF低，那么在晶体中这种离子的弗仑克尔缺陷就占优势。

2）肖特基缺陷

同样，先考虑单质晶体。肖特基缺陷只有空位，没有间隙原子。我们仍然作和弗仑克尔缺陷一样的假设则在N个点阵位置中，产生n个空位的组合方式也如式（4-2）所示。与弗仑克尔缺陷不同的是，没有间隙原子的排布，故产生n个空位的ΔS为式（4-9）的前三项

在求ΔH时，假设产生一个肖特基空位的形成能为hS，则产生n个空位所需能量为

将式（4-18）和式（4-19）代入ΔG=ΔH-TΔS，晶体的吉布斯自由能增量为

在一定温度下达成平衡时，求极值：

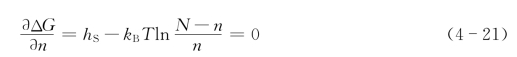
同样，n≪N，所以N-n≈N，式（4-21）变为

整理后得

式（4-23）为单质晶体在一定温度下产生n个肖特基缺陷的平衡摩尔分数。

而对于离子晶体，正、负离子空位成对出现。在推导它们的肖特基缺陷时，与弗仑克尔缺陷类似，要考虑正离子空位和负离子空位的排布引起的熵增，总的微态数可表示为W=W+W-。请读者自行推导，其缺陷的平衡摩尔分数为

3）只有间隙原子的弗仑克尔缺陷

如图4.4（c）所示，假设晶体有N′个间隙位，有n个间隙原子，n≪N′。n个原子在N′个间隙位的组合方式有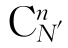种。结果，其ΔS为式（4-9）的后三项，即

假设产生一个间隙原子的形成能为hi，则产生n个间隙原子所需能量为

将式（4-25）和式（4-26）代入ΔG=ΔH-TΔS，晶体的吉布斯自由能增量为

由∂ΔG/∂n=0，且n≪N′，得

综合式（4-17）、式（4-23）、式（4-24）和式（4-28），热缺陷的平衡摩尔分数可统一写成

与Arrhenius方程A exp（-Ea/（kBT））作对比，u为缺陷活化能；根据前面的推导，我们可知热缺陷的活化能与形成能有联系。由式（4-17）知，弗仑克尔缺陷的活化能为形成能的一半即u=hF/2；由式（4-23）知，单质晶体的肖特基缺陷活化能就是其形成能u=hS；由式（4-24）知，二元离子晶体的肖特基缺陷活化能为其形成能的一半即u=hS/2；由式（4-28）知，只有间隙原子的弗仑克尔缺陷，其活化能为其形成能u=hi。

式（4-29）中，A为材料常数，它与缺陷附近的原子振动频率之变化对熵的贡献有关。我们在前文做了点缺陷对点阵振动频率无影响的假设，故这部分的ΔS为零，由此得到A=1。如果要考虑除前面介绍的构型熵外的其他熵增，则A值在大多数情况下处于1～100之间。

4）影响热缺陷平衡摩尔分数的主要因素

由式（4-29）我们可知这些主要因素有以下几方面。

（1）温度。温度升高，热缺陷平衡摩尔分数也增加，故通过控制温度来控制晶体中的热缺陷是一种常用方法。

（2）缺陷形成能。形成能大，说明形成缺陷所需能量高，比较难形成。而形成能主要与晶体结构、晶体组成和离子极化等因素有关。NaCl结构比较致密，只有较小的四面体空隙空着，故较难生成弗仑克尔缺陷，弗仑克尔缺陷在NaCl结构中的形成能约7～8 eV。即使在2000℃，间隙离子的浓度也难以测量。而CaF2结构中的八面体空隙全空着，生成间隙离子较容易。生成间隙F离子F′i的形成能为2.8 eV，而生成肖特基缺陷的形成能为5.5 eV。

通常，弗仑克尔缺陷因有间隙原子产生，其形成能较肖特基缺陷大，特别是结构比较致密的晶体。因此，肖特基缺陷的形成比较容易。

例4.1 Cu晶体单原子的肖特基空位形成能为0.9 eV。计算500℃时，每立方米Cu的平衡空位的摩尔分数及空位数目。A取1，Cu的摩尔质量M=63.54 g/mol，密度为8.96×106g/m3。

解：根据式（4-23），25℃时肖特基缺陷的平衡摩尔分数为

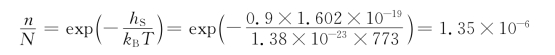
即在500℃时，每100万个原子中才有约1.35个空位。由此可见，热缺陷确实非常少。

要计算空位数目n，根据平衡摩尔分数的关系式n/N，我们需要知道总原子数N。由密度关系式：

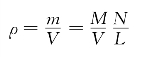
式中，L为阿伏伽德罗常数；V=1，则总原子数N为

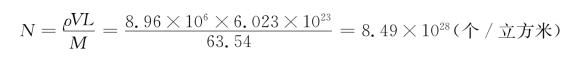
则空位数目n=8.49×1028×1.35×10-6=1.15×1023（个/立方米）。

例4.2 MgO晶体中，肖特基缺陷的形成能为6 eV，分别计算在25℃和1600℃时的肖特基缺陷平衡摩尔分数，其中A取1。

解：根据式（4-24），25℃时肖特基缺陷平衡摩尔分数为

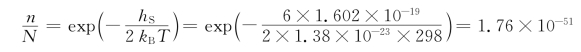
1600℃时肖特基缺陷平衡摩尔分数为

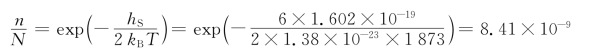
由上述可见，在低温下，热缺陷非常少。随着温度升高，热缺陷增加较多。

除了这些本征热缺陷外，在材料学科领域，更重要的是掺杂引入的杂质缺陷。引入的杂质原子不仅会进入间隙位，还会取代基体材料中正常格点处的原子。我们可把晶体（尤其是离子晶体）中的点缺陷看作是一种化学物质。这样就可像化学反应一样，用热力学函数、质量作用定律、平衡常数之类的概念来研究缺陷。既然要像化学反应式一样来研究缺陷，就需要一个缺陷之间的反应式，即缺陷反应式。