数学期望描述了随机变量取值的“平均”.有时仅知道这个平均值还不够.例如,有A,B 两名射手,他们每次射击命中的环数分别记为X,Y,已知X,Y 的分布律分别如表4.8 和表4.9 所示.
表4.8

表4.9

由于E(X)=E(Y)=9 环,可见从均值的角度是分不出谁的射击技术更高,故还需考虑其他的因素.通常的想法是:在射击平均环数相等的条件下,进一步衡量谁的射击技术更稳定些.也就是看谁命中的环数比较集中于平均值的附近,通常人们会采用命中的环数X 与它的平均值E(X)之间的离差 X-E(X)
X-E(X)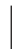 的均值E[
的均值E[ X-E(X)
X-E(X) ]来度量,E[
]来度量,E[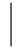 X-E(X)
X-E(X) ]越小,表明X的值越集中于E(X)的附近,即技术稳定.E[
]越小,表明X的值越集中于E(X)的附近,即技术稳定.E[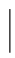 X-E(X)
X-E(X)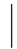 ]越大,表明X 的值越分散,即技术不稳定.但由于E[
]越大,表明X 的值越分散,即技术不稳定.但由于E[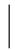 X-E(X)
X-E(X)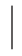 ]带有绝对值,运算不便,故通常采用X 与E(X)之间的离差
]带有绝对值,运算不便,故通常采用X 与E(X)之间的离差 X-E(X)
X-E(X)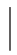 平方的平均值E{[X-E(X)]2}来度量随机变量X 取值的离散程度.上例中,由于
平方的平均值E{[X-E(X)]2}来度量随机变量X 取值的离散程度.上例中,由于
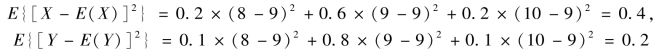
由此可见B 的技术更稳定些.
定义4.3 设X 是一个随机变量,若E[X-E(X)]2 存在,则称E[X-E(X)]2 为随机变量X 的方差(variance),记为D(X)或Var(X),即
![]()
![]() 称为X 的标准差(standard deviation)或均方差(mean square deviation),记为σ(X).
称为X 的标准差(standard deviation)或均方差(mean square deviation),记为σ(X).
可见,方差就是随机变量X 与其“中心”E(X)的偏差平方的平均.随机变量的方差总是一个非负数.若X 取值密集在它的均值周围,则方差较小.若X 取值比较分散,则方差较大.所以,方差是衡量随机变量在其均值周围取值分散程度的一个数量指标.
由随机变量函数的期望公式,我们有
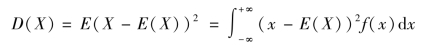
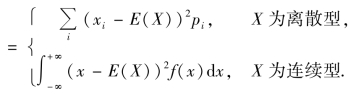
另一个关系式是D(X)=E(X2)-[E(X)]2
因为
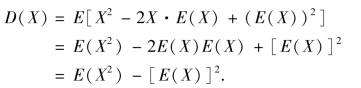
例4.10(仪器选择问题) 分别用X 和Y 两种测量仪器多次测量某一零件的直径,结果分别如表4.10 和表4.11 所示.(https://www.daowen.com)
表4.10

表4.11

试比较这两种仪器的优劣.
解 用随机变量X 和Y 的数学期望和方差作比较
E(X)=118 ×0.06+119 ×0.14+120 ×0.60+121 ×0.05=119.9,
D(X)=E(X2)-[E(X)]2≈14 398.3.
E(Y)=118 ×0.09+119 ×0.15+120 ×0.52+121 ×0.16=119.9,
D(Y)=E(Y2)-[E(Y)]2≈14 398.6.
计算结果表明,
![]()
所以X 仪器的稳定性好于Y 仪器.
例4.11 设随机变量X 的概率密度为
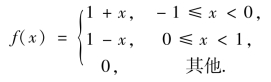
求D(X).
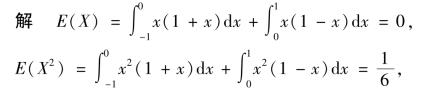
于是,D(X)=E(X2)-[E(X)]2=![]() .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







