单个正态总体数学期望的假设检验

（1）σ2 已知，关于μ 的假设检验[U 检验法（U-test）]

设总体X~N（μ，σ2），方差σ2 已知，检验假设

由

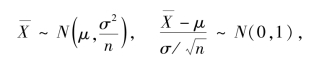
我们选取

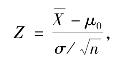
作为此假设检验的统计量，显然当假设H0 为真（即μ=μ0 正确）时，Z ~N（0，1），所以对于给定的显著性水平α，可求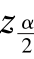使

如图8.1 所示，即

从而有

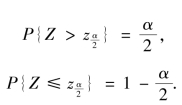
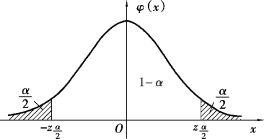
图8.1

利用概率1-，反查标准正态分布函数表，得上α 分位点（即临界值）及上1-分位点（即临界值）-.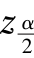

另一方面，利用样本观察值x1，x2，…，xn 计算统计量Z 的观察值

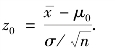
如果：①，则在显著性水平α 下，拒绝原假设H0（接受备择假设H1），所以便是H0 的拒绝域.

②，则在显著性水平α 下，接受原假设H0，认为H0 正确.

这里我们是利用H0 为真时服从N（0，1）分布的统计量Z 来确定拒绝域的，这种检验法称为U 检验法（或称Z 检验法）.例8.1 中所用的方法就是U 检验法.为了熟悉这类假设检验的具体做法，现在我们再举两例.

例8.2　在正常情况下，茅台酒厂某车间使用灌装机生产的茅台酒容量服从N（500，1），某天计量检验人员随机抽取10 瓶酒，算得平均重量499.3 mL，问这天机器是否正常？

解　①提出假设.

②检验统计量.

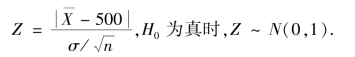
③H0 的拒绝域.给定α=0.05，C：=z0.025=1.96.

④取样判定.Z=

故拒绝H0，即这天机器工作不正常.

例8.3　根据长期经验和资料的分析，某砖厂生产的砖的“抗断强度”X 服从正态分布，方差σ2=1.21.从该厂产品中随机抽取6 块，测得抗断强度如下（单位：kg·cm -2）：

检验这批砖的平均抗断强度为32.50 kg·cm -2是否成立（取α=0.05，并假设砖的抗断强度的方差不会有什么变化）？

解　①提出假设.

②选取统计量

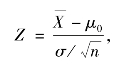
若H0 为真，则Z~N（0，1）.

③对给定的显著性水平α=0.05，求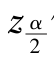使

这里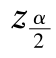=z0.025=1.96.

④计算统计量Z 的观察值

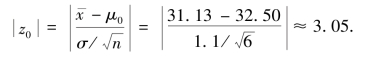
⑤判断：由于=3.05 >z0.025=1.96，所以在显著性水平α=0.05 下否定H0，即不能认为这批产品的平均抗断强度是32.50 kg·cm -2.

把上面的检验过程加以概括，得到了关于方差已知的正态总体期望值μ 的检验步骤：

①提出待检验的假设H0：μ=μ0.H1：μ≠μ0.

②构造统计量Z，并计算其观察值z0：

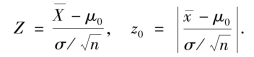
③对给定的显著性水平α，根据

查标准正态分布表，得双侧α 分位点.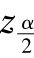

④做出判断：根据H0 的拒绝域

若，则拒绝H0，接受H1.

若，则接受H0.

（2）方差σ2 未知，检验μ （t 检验法（t-test））

设总体X~N（μ，σ2），方差σ2 未知，检验

由于σ2 未知，便不是统计量，这时我们自然想到用σ2 的无偏估计量——样本方差S2 代替σ2，由于

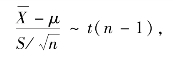
故选取样本的函数

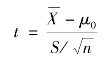
作为统计量，当H0 为真（μ=μ0）时t~t（n-1），对给定的检验显著性水平α，由

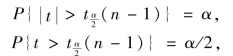(https://www.daowen.com)

如图8.2 所示，直接查t 分布表，得t 分布分位点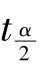（n-1），也称双侧α 分点.

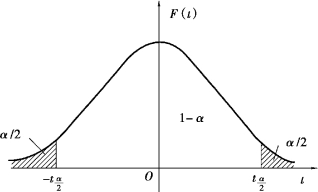
图8.2

利用样本观察值，计算统计量t 的观察值

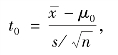
因而原假设H0 的拒绝域为

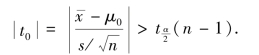
所以，若（n-1），则拒绝H0，接受H1.若（n-1），则接受原假设H0.

上述利用t 统计量得出的检验法称为t 检验法.在实际中，正态总体的方差常为未知，所以我们常用t 检验法来检验关于正态总体均值的问题.

例8.4　设检查某地区新生男婴的体重X 近似服从正态分布，μ，σ 均未知，样本数据选择随机抽取100 个男婴，样本均值为3 350，样本方差为559，在显著性水平α=0.05 下，能否认为该地区男婴体重达到了《世界卫生组织婴儿体重标准》标准体重3 300 g？

解　总体X~N（μ，σ2），μ，σ2 未知.

①H0:μ=μ0=3 300;H1:μ≠μ0.

②检验统计量t=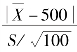，H0 为真时，t~t（99）.

③H0 的拒绝域 给定α=0.05，（99）=1.96.

④取样判定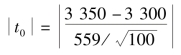=0.894 <1.96.

观察值没有落入拒绝域，故接受H0.

例8.5　用某仪器间接测量温度，重复5 次，所得的数据是

而用别的精确办法测得温度为1 277°（可看作温度的真值），试问此仪器间接测量有无系统偏差？这里假设测量值X 服从N（μ，σ2）分布.

解　问题是要检验

由于σ2 未知（即仪器的精度不知道），选取统计量

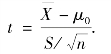
当H0 为真时，t~t（n-1），t 的观察值为

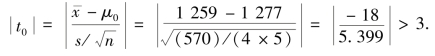
对于给定的检验水平α=0.05，由

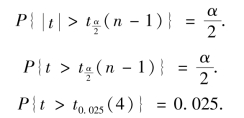
查t 分布表得双侧α 分位点

因为>3 >t0.025（4）=2.776，故应拒绝H0，认为该仪器间接测量有系统偏差.

（3）双边检验与单边检验

上面讨论的假设检验中，H0 为μ=μ0，而备择假设H1：μ≠μ0 意思是μ 可能大于μ0，也可能小于μ0，称为双边备择假设，而称形如H0：μ=μ0，H1：μ≠μ0 的假设检验为双边检验.有时只关心总体均值是否增大，例如，试验新工艺以提高材料的强度，这时所考虑的总体的均值应该越大越好，如果能判断在新工艺下总体均值较以往正常生产的大，则可考虑采用新工艺.此时，需要检验假设

（在这里做了新工艺不可能比旧的更差的假定），形如上式的假设检验，称为右边检验，类似地，有时我们需要检验假设

形如上式的假设检验，称为左边检验，右边检验与左边检验统称为单边检验.

下面来讨论单边检验的拒绝域.

设总体X~N（μ，σ2），σ2 为已知，x1，x2，…，xn 是来自X 的样本观察值.给定显著性水平α，先求检验问题

的拒绝域.

取检验统计量Z=，当H0 为真时，Z 不应太大，而在H1 为真时，由于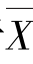是μ 的无偏估计，当μ 偏大时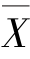，也偏大，从而Z 往往偏大，因此拒绝域的形式为

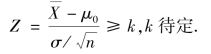
因为当H0 为真时，~N（0，1），由

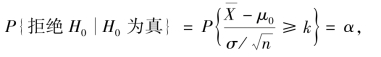
得k=zα，故拒绝域为

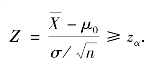
类似地，左边检验问题

的拒绝域为

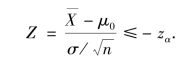
例8.6　从甲地发送一个信号到乙地，设发送的信号值为μ，由于信号传送时有噪声叠加到信号上，这个噪声是随机的，它服从正态分布N（0，22），从而乙地接到的信号值是一个服从正态分布N（μ，22）的随机变量.设甲地发送某信号5 次，乙地收到的信号值为

由以往经验可知，信号值为8，于是乙方猜测甲地发送的信号值为8，能否接受这种猜测？取α=0.05.

解　按题意需检验假设

这是右边检验问题，其拒绝域为

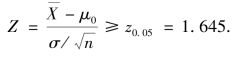
而现在

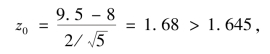
所以拒绝H0，认为发出的信号值μ>8.