祖暅原理：水平面截球体的体积相等

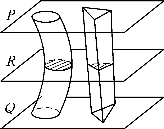
图6

南北朝时期的数学家祖暅（中国古代数学家祖冲之之子，生卒不详）发展了中国古代数学家刘徽（约225—295）的“割圆术”的思想，在求出球的体积的同时，得到了一个重要的结论（后人称之为“祖暅原理”）：“夫叠基成立积，缘幂势既同，则积不容异。”用现在的话来讲，一个几何体（“立积”）是由一系列很薄的小片（“基”）叠成的；若两个几何体相应的小片的面积（“幂势”）都相同，那它们的体积（“积”）必然相等（见图6）。

进一步有：若两个几何体相应的小片的面积（“幂势”）之比等于常数k，则它们的体积（“积”）之比也等于k。

注：西方的著作中常把祖暅原理称为卡瓦列里原理。卡瓦列里（Francesco Bonaventura Cavalieri，1598—1647）是意大利数学家，他提出这一原理比祖暅晚了约2025年。(https://www.daowen.com)

利用祖暅原理可以给出求球体体积的另一解法。

如图7所示，取上半球体｛（x，y，z）|x2+y2+z2≤R2，z≥0｝为第一个几何体，将圆柱体｛（x，y，z）|x2+y2≤R2，0≤z≤R｝挖去倒立的圆锥｛（x，y，z）|x2+y2≤z2，0≤z≤R｝，视为第二个几何体。则对任意的0≤z≤R，过点（0，0，z）作水平面去截这两个几何体，得到的截口面积相等，都是π（R2-z2），由祖暅原理可知这两个几何体的体积相等。由于第二个几何体中的圆柱体与圆锥的体积公式我们都已知道，由此得到半球体的体积为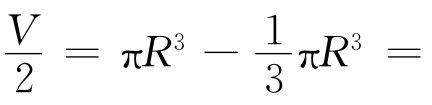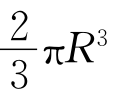，因此球体体积为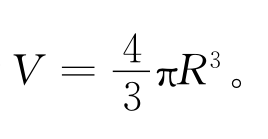

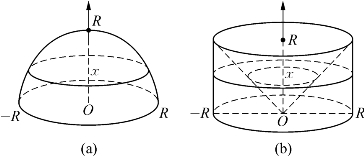
图7