3.13  如何在二叉树中找出路径最大的和

3.13 如何在二叉树中找出路径最大的和

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一棵二叉树，求各个路径的最大和，路径可以以任意结点作为起点和终点。比如给定以下二叉树：

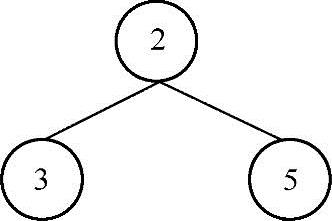
返回10。

分析与解答：

本题可以通过对二叉树进行后序遍历来解决，具体思路如下：

对于当前遍历到的结点root，假设已经求出在遍历root结点前最大的路径和为max。

（1）求出以root.left为起始结点，叶子结点为终结点的最大路径和为maxLeft。

（2）同理求出以root.right为起始结点，叶子结点为终结点的最大路径和maxRight。

包含root结点的最长路径可能包含如下三种情况：

（1）leftMax=root.val+maxLeft（左子树最大路径和可能为负）。

（2）rightMax=root.val+maxRight（右子树最大路径和可能为负）。

（3）allMax=root.val+maxLeft+maxRight（左右子树的最大路径和都不为负）。

因此，包含root结点的最大路径和为tmpMax=max（leftMax，rightMax，allMax）。

在求出包含root结点的最大路径后，如果tmpMax＞max，那么更新最大路径和为tmpMax。

实现代码如下：

程序的运行结果如下：

10

算法性能分析：

二叉树后序遍历的时间复杂度为O（N），因此，这种方法的时间复杂度也为O（N）。