8.6  如何进行希尔排序

8.6 如何进行希尔排序

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用希尔排序对数组进行升序排列。

分析与解答：

希尔排序也称为“缩小增量排序”。它的基本原理是：首先将待排序的元素分成多个子序列，使得每个子序列的元素个数相对较少，对各个子序列分别进行直接插入排序，待整个待排序序列“基本有序后”，再对所有元素进行一次直接插入排序。

具体步骤如下：

1）选择一个步长序列t1，t2，…，tk，满足ti＞tj（i＜j），tk=1。

2）按步长序列个数k，对待排序序列进行k趟排序。

3）每趟排序，根据对应的步长ti，将待排序列分割成ti个子序列，分别对各个子序列进行直接插入排序。

需要注意的是，当步长因子为1时，所有元素作为一个序列来处理，其长度为n。以数组{26，53，67，48，57，13，48，32，60，50}（假设要求为升序排列），步长序列{5，3，1}为例。具体步骤如下：

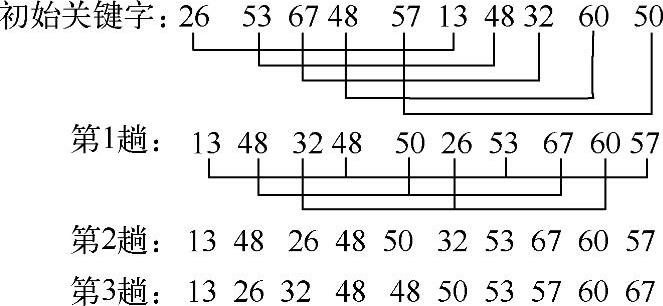
程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

算法性能分析：

希尔排序的关键并不是随便地分组后各自排序，而是将相隔某个“增量”的记录组成一个子序列，实现跳跃式的移动，使得排序的效率提高。希尔排序是一种不稳定的排序方法，平均时间复杂度为O（nlogn），最差情况下的时间复杂度为O（n^s）（1＜s＜2），空间复杂度为O（1）。