面试笔试真题解析篇

面试笔试真题解析篇主要针对近3年以来近百家顶级IT企业的面试笔试算法真题而设计，这些企业涉及业务包括系统软件、搜索引擎、电子商务、手机APP及安全关键软件等，面试笔试真题难易适中，覆盖面广，非常具有代表性与参考性。本篇对这些真题进行了合理地划分与归类（包括链表、栈、队列、二叉树、数组、字符串和海量数据处理等内容），并且对其进行了庖丁解牛式地分析与讲解，针对真题中涉及的部分重难点问题，本篇都进行了适当地扩展与延伸，力求对知识点的讲解清晰而不紊乱，全面而不啰嗦，使得读者能够通过本书不仅获取到求职的知识，同时更有针对性地进行求职准备，最终能够收获一份满意的工作。

第1章 链表

链表作为最基本的数据结构，不仅在实际应用中有着非常重要的作用，而且也是程序员面试笔试中必考的内容。具体而言，它的存储特点是：可以用任意一组存储单元来存储单链表中的数据元素（存储单元可以是不连续的），而且，除了存储每个数据元素a_i外，还必须存储指示其直接后继元素的信息。这两部分信息组成的数据元素a_i的存储映像称为结点。N个结点链在一起被称为链表，结点只包含其后继结点的信息的链表被称为单链表，而链表的第一个结点通常被称为头结点。

对于单链表，又可以将其分为有头结点的单链表和无头结点的单链表，如下图所示。

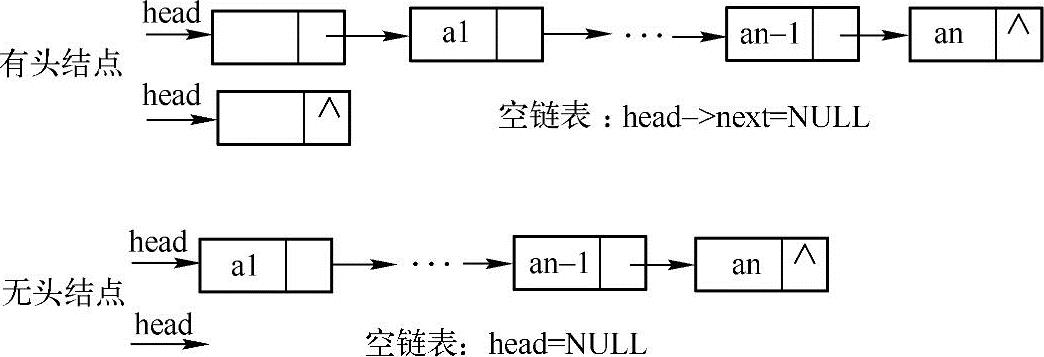
在单链表的开始结点之前附设一个类型相同的结点，称之为头结点，头结点的数据域可以不存储任何信息（也可以存放如线性表的长度等附加信息），头结点的指针域存储指向开始结点的指针（即第一个元素结点的存储位置）。需要注意的是，在Java中没有指针的概念，而类似指针的功能都是通过引用来实现的，为了便于理解，我们仍然使用指针（可以认为引用与指针是类似的）来进行描述，而在实现的代码中，都是通过引用来建立结点之间的关系。

具体而言，头结点的作用主要有以下两点：

（1）对于带头结点的链表，当在链表的任何结点之前插入新结点或删除链表中任何结点时，所要做的都是修改前一个结点的指针域，因为任何结点都有前驱结点。若链表没有头结点，则首元素结点没有前驱结点，在其前面插入结点或删除该结点时操作会复杂些，需要进行特殊的处理。

（2）对于带头结点的链表，链表的头指针是指向头结点的非空指针，因此，对空链表与非空链表的处理是一样的。

由于头结点有诸多的优点，因此，本章中所介绍的算法都使用了带头结点的单链表。

如下是一个单链表数据结构的定义示例：

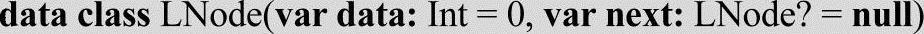
1.1 如何实现链表的逆序

【出自TX笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个带头结点的单链表，请将其逆序。即如果单链表原来为head-＞1-＞2-＞3-＞4-＞5-＞6-＞7，则逆序后变为head-＞7-＞6-＞5-＞4-＞3-＞2-＞1。

分析与解答：

由于单链表与数组不同，单链表中每个结点的地址都存储在其前驱结点的指针域中，因此，对单链表中任何一个结点的访问只能从链表的头指针开始进行遍历。在对链表的操作过程中，需要特别注意在修改结点指针域的时候，记录下后继结点的地址，否则会丢失后继结点。

方法一：就地逆序

主要思路：在遍历链表的时候，修改当前结点的指针域的指向，让其指向它的前驱结点。为此需要用一个指针变量来保存前驱结点的地址。此外，为了在调整当前结点指针域的指向后还能找到后继结点，还需要另外一个指针变量来保存后继结点的地址，在所有的结点都被保存好以后就可以直接完成指针的逆序了。除此之外，还需要特别注意对链表首尾结点的特殊处理。具体实现方式如下图所示。

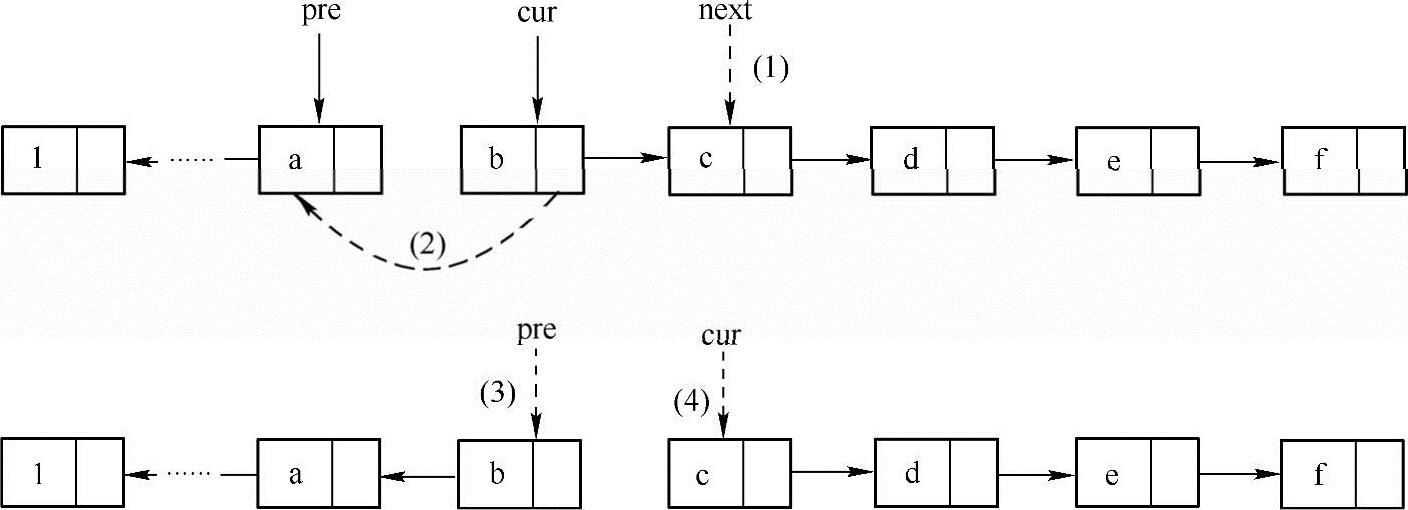
在上图中，假设当前已经遍历到cur结点，由于它所有的前驱结点都已经完成了逆序操作，因此，只需要使cur.next=pre即可完成逆序操作，在此之前为了能够记录当前结点的后继结点的地址，需要用一个额外的指针next来保存后继结点的信息，通过上图中的步骤（1）～（4）把实线的指针调整为虚线的指针就可以完成当前结点的逆序；当前结点完成逆序后，通过向后移动指针来对后续的结点用同样的方法进行逆序操作。算法实现如下：

程序的运行结果如下：

逆序前：0 1 2 3 4 5 6 7

逆序后：7 6 5 4 3 2 1 0

算法性能分析：

以上这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（N），其中，N为链表的长度。但是需要常数个额外的变量来保存当前结点的前驱结点与后继结点，因此，空间复杂度为O（1）。

方法二：递归法

假定原链表为1-＞2-＞3-＞4-＞5-＞6-＞7，递归法的主要思路：先逆序除第一个结点以外的子链表（将1-＞2-＞3-＞4-＞5-＞6-＞7变为1-＞7-＞6-＞5-＞4-＞3-＞2），接着把结点1添加到逆序的子链表的后面（1-＞7-＞6-＞5-＞4-＞3-＞2变为7-＞6-＞5-＞4-＞3-＞2-＞1）。同理，在逆序链表2-＞3-＞4-＞5-＞6-＞7时，也是先逆序子链表3-＞4-＞5-＞6-＞7（逆序为2-＞7-＞6-＞5-＞4-＞3），接着实现链表的整体逆序（2-＞7-＞6-＞5-＞4-＞3转换为7-＞6-＞5-＞4-＞3-＞2）。实现代码如下：

算法性能分析：

由于递归法也只需要对链表进行一次遍历，因此，算法的时间复杂度也为O（N），其中，N为链表的长度。递归法的主要优点是思路比较直观，容易理解，而且也不需要保存前驱结点的地址；缺点是算法实现的难度较大，此外，由于递归法需要不断地调用自己，需要额外的压栈与弹栈操作，因此，与方法一相比性能会有所下降。

方法三：插入法

插入法的主要思路：从链表的第二个结点开始，把遍历到的结点插入到头结点的后面，直到遍历结束。假定原链表为head-＞1-＞2-＞3-＞4-＞5-＞6-＞7，在遍历到2的时候，将其插入到头结点后，链表变为head-＞2-＞1-＞3-＞4-＞5-＞6-＞7，同理将后序遍历到的所有结点都插入到头结点head后，就可以实现链表的逆序。实现代码如下：

算法性能分析：

以上这种方法也只需要对单链表进行一次遍历，因此，时间复杂度为O（N），其中，N为链表的长度。与方法一相比，这种方法不需要保存前驱结点的地址，与方法二相比，这种方法不需要递归地调用，效率更高。

引申：

（1）对不带头结点的单链表进行逆序

（2）从尾到头输出链表

分析与解答：

对不带头结点的单链表的逆序读者可以自己练习（方法二已经实现了递归的方法），这里主要介绍单链表逆向输出的方法。

方法一：就地逆序+顺序输出

首先对链表进行逆序，然后顺序输出逆序后的链表。这种方法的缺点是改变了链表原来的结构。

方法二：逆序+顺序输出

申请新的存储空间，对链表进行逆序，然后顺序输出逆序后的链表。逆序的主要思路：每当遍历到一个结点的时候，申请一块新的存储空间来存储这个结点的数据域，同时把新结点插入到新的链表的头结点后。这种方法的缺点是需要申请额外的存储空间。

方法三：递归输出

递归输出的主要思路：先输出除当前结点外的后继子链表，然后输出当前结点，假如链表为：1-＞2-＞3-＞4-＞5-＞6-＞7，那么先输出2-＞3-＞4-＞5-＞6-＞7，再输出1。同理，对于链表2-＞3-＞4-＞5-＞6-＞7，也是先输出3-＞4-＞5-＞6-＞7，接着输出2，直到遍历到链表的最后一个结点7的时候会输出结点7，然后递归地输出6，5，…，1。实现代码如下：

程序的运行结果如下：

顺序输出：0 1 2 3 4 5 6 7

逆序输出：7 6 5 4 3 2 1 0

算法性能分析：

以上这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（N），其中，N为链表的长度。

1.2 如何从无序链表中移除重复项

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个没有排序的链表，去掉其重复项，并保留原顺序，例如链表1-＞3-＞1-＞5-＞5-＞7，去掉重复项后变为1-＞3-＞5-＞7。

分析与解答：

方法一：顺序删除

主要思路：通过双重循环直接在链表上进行删除操作。外层循环用一个指针从第一个结点开始遍历整个链表，然后内层循环用另外一个指针遍历其余结点，将与外层循环遍历到的指针所指结点的数据域相同的结点删除。如下图所示：

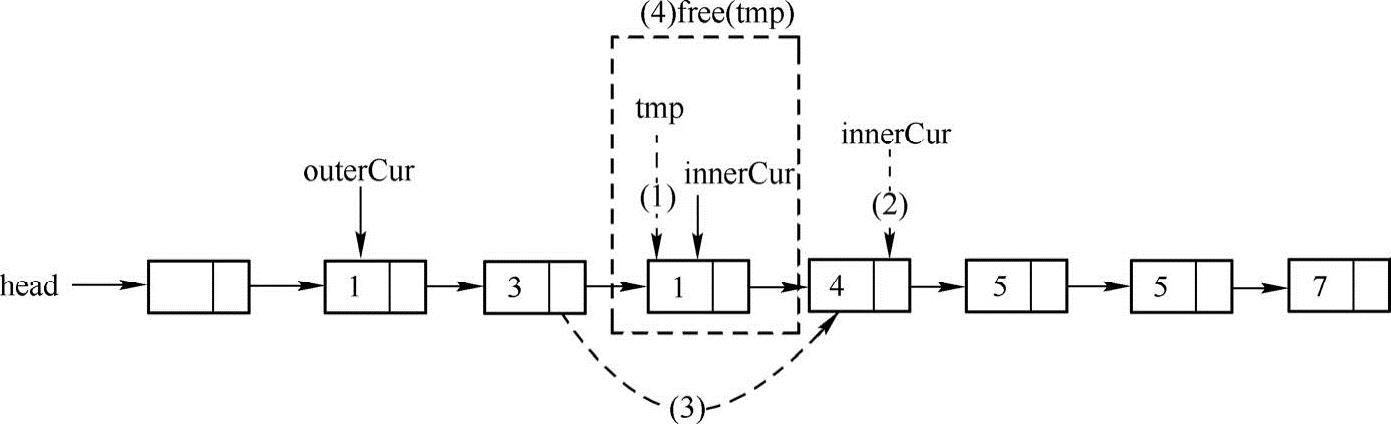
假设外层循环从outerCur开始遍历，当内层循环指针innerCur遍历到上图实线所示的位置（outerCur.data==innerCur.data）时，需要把innerCur指向的结点删除。具体步骤如下：

（1）用tmp记录待删除的结点的地址。

（2）为了能够在删除tmp结点后继续遍历链表中其余的结点，使innerCur指向它的后继结点：innerCur=innerCur.next。

（3）从链表中删除tmp结点。

实现代码如下：

程序的运行结果如下：

删除重复结点前：1 3 1 5 5 7

删除重复结点后：1 3 5 7

算法性能分析：

由于这种方法采用双重循环对链表进行遍历，因此，时间复杂度为O（N^2），其中，N为链表的长度，在遍历链表的过程中，使用了常量个额外的指针变量来保存当前遍历的结点、前驱结点和被删除的结点，因此，空间复杂度为O（1）。

方法二：递归法

主要思路：对于结点cur，首先递归地删除以cur.next为首的子链表中重复的结点，接着从以cur.next为首的子链表中找出与cur有着相同数据域的结点并删除，实现代码如下：

算法性能分析：

这种方法与方法一类似，从本质上而言，由于这种方法需要对链表进行双重遍历，因此，时间复杂度为O（N^2），其中，N为链表的长度。由于递归法会增加许多额外的函数调用，因此，从理论上讲，该方法效率比方法一低。

方法三：空间换时间

通常情况下，为了降低时间复杂度，往往在条件允许的情况下，通过使用辅助空间实现。具体而言，主要思路如下：

（1）建立一个HashSet，HashSet中的内容为已经遍历过的结点内容，并将其初始化为空。

（2）从头开始遍历链表中的所以结点，存在以下两种可能性：

1）如果结点内容已经在HashSet中，则删除此结点，继续向后遍历。

2）如果结点内容不在HashSet中，则保留此结点，将此结点内容添加到HashSet中，继续向后遍历。

引申：如何从有序链表中移除重复项

分析与解答：

上述介绍的方法也适用于链表有序的情况，但是由于以上方法没有充分利用到链表有序这个条件，因此，算法的性能肯定不是最优的。本题中，由于链表具有有序性，因此，不需要对链表进行两次遍历。所以，有如下思路：用cur指向链表第一个结点，此时需要分为以下两种情况讨论：

（1）如果cur.data==cur.next.data，那么删除cur.next结点。

（2）如果cur.data！=cur.next.data，那么cur=cur.next，继续遍历其余结点。

1.3 如何计算两个单链表所代表的数之和

【出自HW笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定两个单链表，链表的每个结点代表一位数，计算两个数的和。例如：输入链表（3-＞1-＞5）和链表（5-＞9-＞2），输出：8-＞0-＞8，即513+295=808，注意个位数在链表头。

分析与解答：

方法一：整数相加法

主要思路：分别遍历两个链表，求出两个链表所代表的整数的值，然后把这两个整数进行相加，最后把它们的和用链表的形式表示出来。这种方法的优点是计算简单，但是有个非常大的缺点：当链表所代表的数很大的时候（超出了longint的表示范围），就无法使用这种方法了。

方法二：链表相加法

主要思路：对链表中的结点直接进行相加操作，把相加的和存储到新的链表中对应的结点中，同时还要记录结点相加后的进位。如下图所示：

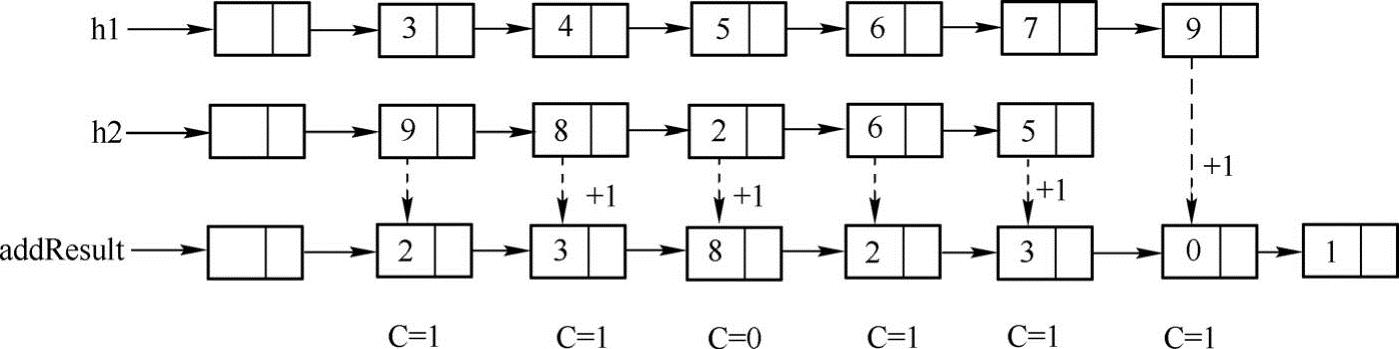
使用这种方法需要注意以下几个问题：

（1）每组结点进行相加后需要记录其是否有进位。

（2）如果两个链表h1与h2的长度不同（长度分别为L1和L2，且L1＜L2），当对链表的第L1位计算完成后，接下来只需要考虑链表L2剩余的结点的值（需要考虑进位）。

（3）对链表所有结点都完成计算后，还需要考虑此时是否还有进位，如果有进位，则需要增加新的结点，此结点的数据域为1。实现代码如下：

程序的运行结果如下：

Head1：3 4 5 6 7 8

Head2：9 8 7 6 5

相加后：2 3 3 3 3 9

运行结果分析：

前五位可以按照整数相加的方法依次从左到右进行计算，第五位7+5+1（进位）的值为3，进位为1。此时Head2已经遍历结束，由于Head1还有结点没有被遍历，所以，依次接着遍历Head1剩余的结点：8+1（进位）=9，没有进位。因此，运行代码可以得到上述结果。

算法性能分析：

由于这种方法需要对两个链表都进行遍历，因此，时间复杂度为O（N），其中，N为较长的链表的长度，由于计算结果保存在一个新的链表中，因此，空间复杂度也为O（N）。

1.4 如何对链表进行重新排序

【出自WR笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定链表L0-＞L1-＞L2…Ln-1-＞Ln，把链表重新排序为L0-＞Ln-＞L1-＞Ln-1-＞L2-＞Ln-2…。要求：（1）在原来链表的基础上进行排序，即不能申请新的结点；（2）只能修改结点的next域，不能修改数据域。

分析与解答：

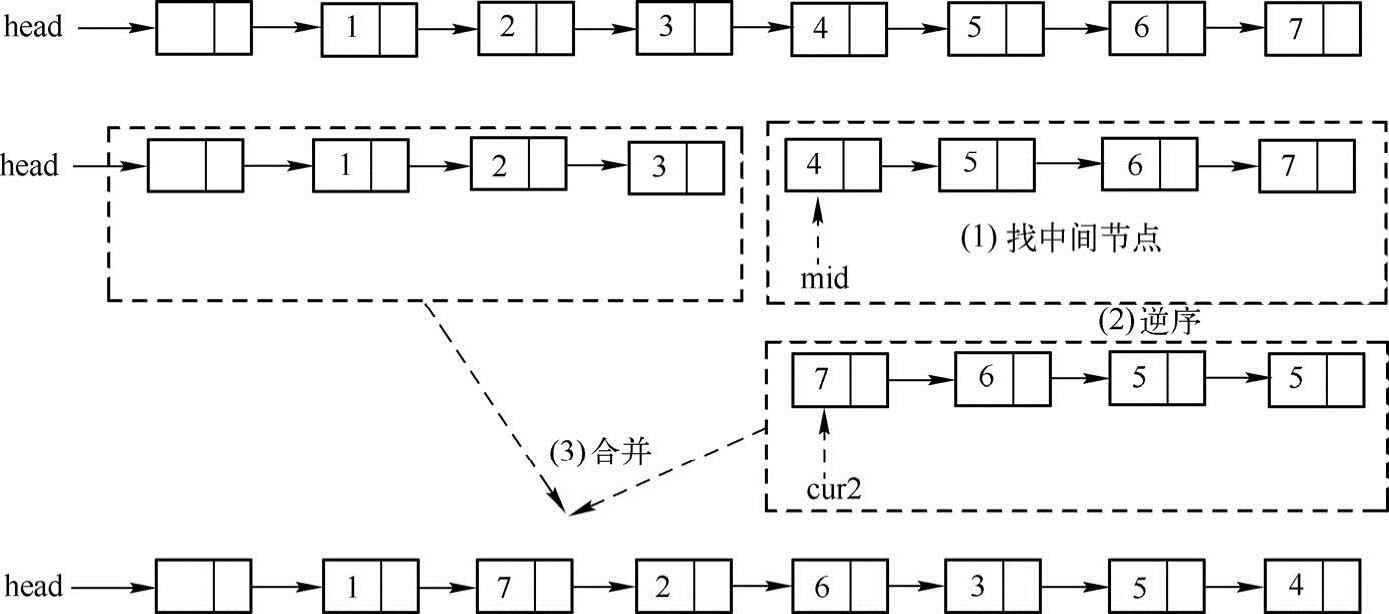
主要思路：（1）首先找到链表的中间结点。（2）对链表的后半部分子链表进行逆序。（3）把链表的前半部分子链表与逆序后的后半部分子链表进行合并，合并的思路：分别从两个链表各取一个结点进行合并。实现方法如下图所示：

实现代码如下：

程序的运行结果如下：

排序前：1 2 3 4 5 6 7

排序后：1 7 2 6 3 5 4

算法性能分析：

查找链表的中间结点的方法的时间复杂度为O（N），逆序子链表的时间复杂度也为O（N），合并两个子链表的时间复杂度也为O（N），因此，整个方法的时间复杂度为O（N），其中，N表示的是链表的长度。由于这种方法只用了常数个额外指针变量，因此，空间复杂度为O（1）。

引申：如何查找链表的中间结点

分析与解答：

主要思路：用两个指针从链表的第一个结点开始同时遍历结点，一个快指针每次走2步，另外一个慢指针每次走1步；当快指针先到链表尾部时，慢指针则恰好到达链表中部。（快指针到链表尾部时，当链表长度为奇数时，慢指针指向的即是链表中间指针，当链表长度为偶数时，慢指针指向的结点和慢指针指向结点的下一个结点都是链表的中间结点），上面的代码FindMiddleNode就是用来求链表的中间结点的。

1.5 如何找出单链表中的倒数第k个元素

【出自WR笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★★

题目描述：

找出单链表中的倒数第k个元素，例如给定单链表：1-＞2-＞3-＞4-＞5-＞6-＞7，则单链表的倒数第k=3个元素为5。

分析与解答：

方法一：顺序遍历两遍法

主要思路：首先遍历一遍单链表，求出整个单链表的长度n，然后把求倒数第k个元素转换为求顺数第n-k个元素，再去遍历一次单链表就可以得到结果。但是该方法需要对单链表进行两次遍历。

方法二：快慢指针法

由于单链表只能从头到尾依次访问链表的各个结点，因此，如果要找链表的倒数第k个元素，也只能从头到尾进行遍历查找，在查找过程中，设置两个指针，让其中一个指针比另一个指针先前移k步，然后两个指针同时往前移动。循环直到先行的指针值为null时，另一个指针所指的位置就是所要找的位置。程序代码如下：

程序的运行结果如下：

链表：1 2 3 4 5 6 7

链表倒数第3个元素为：5

算法性能分析：

这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（N）。另外，由于只需要常量个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

引申：如何将单链表向右旋转K个位置

题目描述：给定单链表1-＞2-＞3-＞4-＞5-＞6-＞7，k=3，那么旋转后的单链表变为5-＞6-＞7-＞1-＞2-＞3-＞4。

分析与解答：

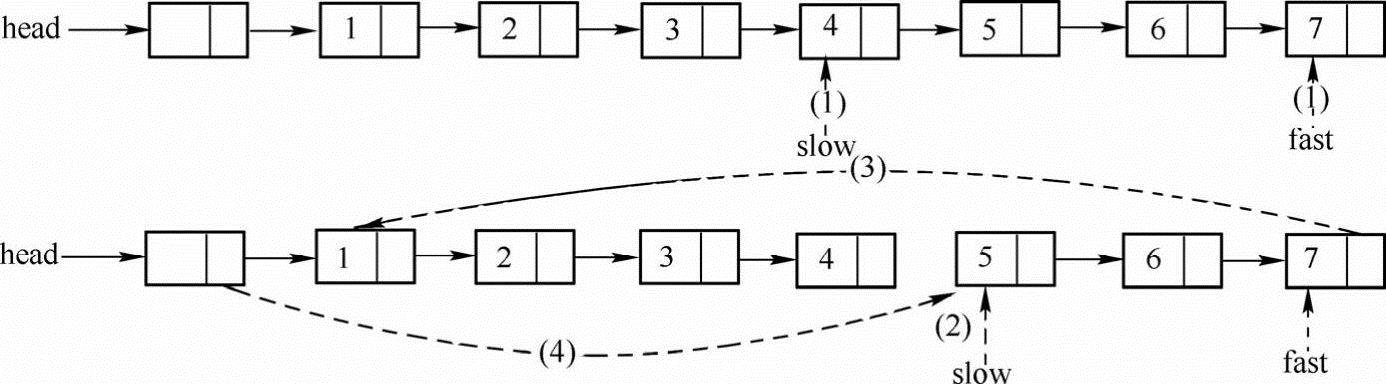
主要思路：（1）首先找到链表倒数第k+1个结点slow和尾结点fast（如下图所示）。（2）把链表断开为两个子链表，其中，后半部分子链表结点的个数为k。（3）使原链表的尾结点指向链表的第一个结点。（4）使链表的头结点指向原链表倒数第k个结点。

实现代码如下：

程序的运行结果如下：

旋转前：1 2 3 4 5 6 7

旋转后：5 6 7 1 2 3 4

算法性能分析：

这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（n）。另外，由于只需要几个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

1.6 如何检测一个较大的单链表是否有环

【出自ALBB笔试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

单链表有环指的是单链表中某个结点的next域指向的是链表中在它之前的某一个结点，这样在链表的尾部形成一个环形结构。如何判断单链表是否有环存在？

分析与解答：

方法一：蛮力法

定义一个HashSet用来存放结点的引用，并将其初始化为空，从链表的头结点开始向后遍历，每遍历到一个结点就判断HashSe中是否有这个结点的引用，如果没有，说明这个结点是第一次访问，还没有形成环，那么将这个结点的引用添加到指针HashSet中去。如果在HashSet中找到了同样的结点，那么说明这个结点已经被访问过了，于是就形成了环。这种方法的时间复杂度为O（N），空间复杂度也为O（N）。

方法二：快慢指针遍历法

定义两个指针fast（快）与slow（慢），二者的初始值都指向链表头，指针slow每次前进一步，指针fast每次前进两步，两个指针同时向前移动，快指针每移动一次都要跟慢指针比较，如果快指针等于慢指针，就证明这个链表是带环的单向链表，否则，证明这个链表是不带环的循环链表。实现代码见后面引申部分。

引申：如果链表存在环，那么如何找出环的入口点

分析与解答：

当链表有环的时候，如果知道环的入口点，那么在需要遍历链表或释放链表所占的空间的时候，方法将会非常简单，下面主要介绍查找链表环入口点的思路。

如果单链表有环，那么按照上述方法二的思路，当走得快的指针fast与走得慢的指针slow相遇时，slow指针肯定没有遍历完链表，而fast指针已经在环内循环了n圈（1＜=n）。如果slow指针走了s步，则fast指针走了2s步（fast步数还等于s加上在环上多转的n圈），假设环长为r，则满足如下关系表达式：

2s=s+nr

由此可以得到：s=nr

设整个链表长为L，入口环与相遇点距离为x，起点到环入口点的距离为a。则满足如下关系表达式：

a+x=nr

a+x=（n-1）r+r=（n-1）r+L-a

a=（n-1）r+（L-a-x）

（L-a-x）为相遇点到环入口点的距离，从链表头到环入口点的距离=（n-1）*环长+相遇点到环入口点的长度，于是从链表头与相遇点分别设一个指针，每次各走一步，两个指针必定相遇，且相遇第一点为环入口点。实现代码如下：

程序的运行结果如下：

有环

环的入点为：3

运行结果分析：

示例代码中给出的链表为：1-＞2-＞3-＞4-＞5-＞6-＞7-＞3（3实际代表链表第三个结点）。因此，IsLoop函数返回的结果为两个指针相遇的结点，所以，链表有环，通过函数FindLoopNode可以获取到环的入口点为3。

算法性能分析：

这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（n）。另外由于只需要几个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

1.7 如何把链表相邻元素翻转

【出自TX笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

把链表相邻元素翻转，例如给定链表为1-＞2-＞3-＞4-＞5-＞6-＞7，则翻转后的链表变为2-＞1-＞4-＞3-＞6-＞5-＞7。

分析与解答：

方法一：交换值法

最容易想到的方法就是交换相邻两个结点的数据域，这种方法由于不需要重新调整链表的结构，因此，比较容易实现，但是这种方法并不是考官所期望的解法。

方法二：就地逆序

主要思路：通过调整结点指针域的指向来直接调换相邻的两个结点。如果单链表恰好有偶数个结点，那么只需要将奇偶结点对调即可，如果链表有奇数个结点，那么只需要将除最后一个结点外的其他结点进行奇偶对调即可。为了便于理解，下图给出了其中第一对结点对调的方法。

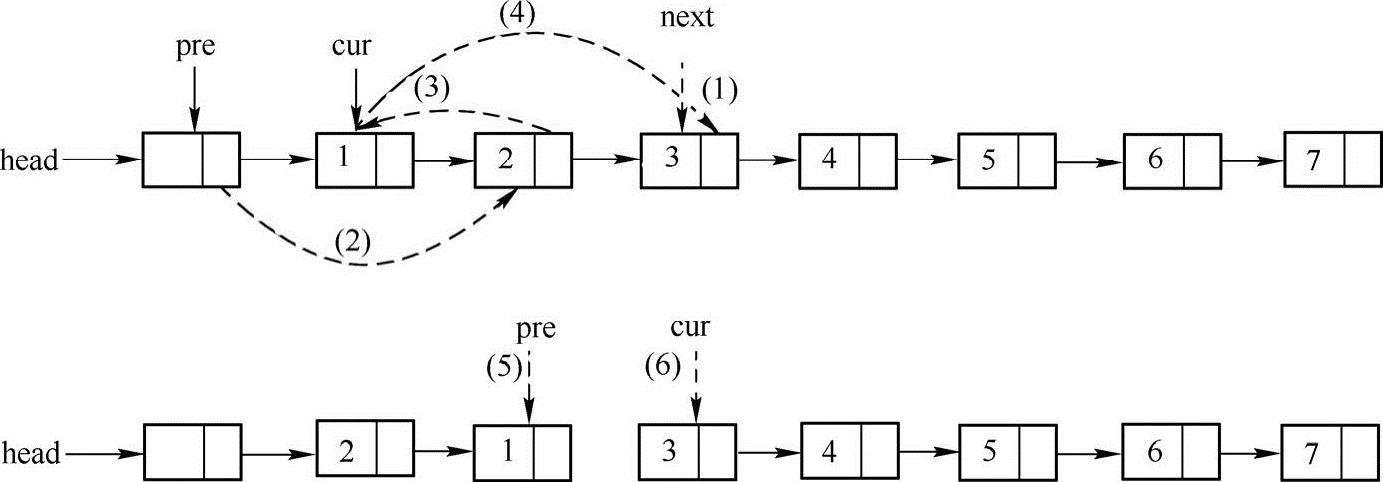
在上图中，当前遍历到结点cur，通过（1）～（6）6个步骤用虚线的指针来代替实线的指针实现相邻结点的逆序。其中，（1）～（4）实现了前两个结点的逆序操作，（5）和（6）两个步骤向后移动指针，接着可以采用同样的方式实现后面两个相邻结点的逆序操作。实现代码如下：

程序的运行结果如下：

顺序输出：1 2 3 4 5 6 7

逆序输出：2 1 4 3 6 5 7

上例中，由于链表有奇数个结点，因此，链表前三对结点相互交换，而最后一个结点保持在原来的位置。

算法性能分析：

这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（n）。另外由于只需要几个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

1.8 如何把链表以K个结点为一组进行翻转

【出自MT笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

K链表翻转是指把每K个相邻的结点看成一组进行翻转，如果剩余结点不足K个，则保持不变。假设给定链表1-＞2-＞3-＞4-＞5-＞6-＞7和一个数K，如果K的值为2，那么翻转后的链表为2-＞1-＞4-＞3-＞6-＞5-＞7。如果K的值为3，那么翻转后的链表为3-＞2-＞1-＞6-＞5-＞4-＞7。

分析与解答：

主要思路：首先把前K个结点看成一个子链表，采用前面介绍的方法进行翻转，把翻转后的子链表链接到头结点后面，然后把接下来的K个结点看成另外一个单独的链表进行翻转，把翻转后的子链表链接到上一个已经完成翻转子链表的后面。具体实现方法如下图所示。

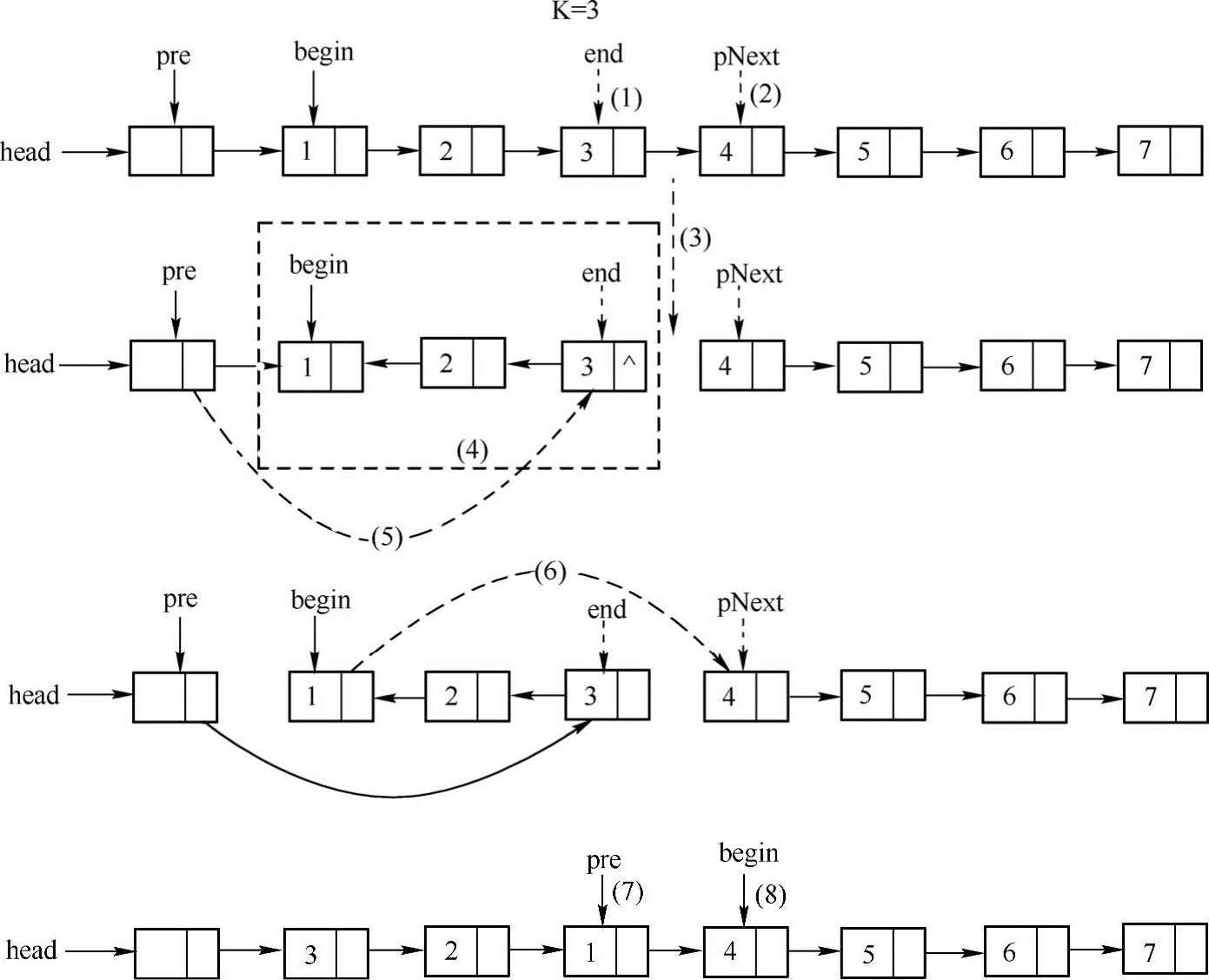
下面K=3为例介绍具体实现的方法：

（1）首先设置pre指向头结点，然后让begin指向链表第一个结点，找到从begin开始第K=3个结点end。

（2）为了采用本章第一节中链表翻转的算法，需要使end.next=null，在此之前需要记录下end指向的结点，用pNext来记录。

（3）使end.next=null，从而使得从begin到end为一个单独的子链表，从而可以对这个子链表采用1.1节介绍的方法进行翻转。

（4）对以begin为第一个结点，end为尾结点所对应的K=3个结点进行翻转。

（5）由于翻转后子链表的第一个结点从begin变为end，因此，执行pre.next=end，把翻转后的子链表链接起来。

（6）把链表中剩余的还未完成翻转的子链表链接到已完成翻转的子链表后面（主要是针对剩余的结点的个数小于K的情况）。

（7）让pre指针指向已完成翻转的链表的最后一个结点。

（8）让begin指针指向下一个需要被翻转的子链表的第一个结点（通过begin=pNext来实现）。

接下来可以反复使用步骤（1）～（8）对链表进行翻转。实现代码如下：

程序的运行结果如下：

顺序输出：1 2 3 4 5 6 7

逆序输出：3 2 1 6 5 4 7

运行结果分析：

由于K=3，因此，链表可以分成三组（123）、（456）、（7）。对（123）翻转后变为（3 21），对（456）翻转后变为（654），由于（7）这个子链表只有1个结点（小于3个），因此，不进行翻转，所以，翻转后的链表就变为3-＞2-＞1-＞6-＞5-＞4-＞7。

算法性能分析：

这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（n）。另外由于只需要几个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

1.9 如何合并两个有序链表

【出自ALBB笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

已知两个链表head1和head2各自有序（例如升序排列），请把它们合并成一个链表，要求合并后的链表依然有序。

分析与解答：

分别用指针head1、head2来遍历两个链表，如果当前head1指向的数据小于head2指向的数据，则将head1指向的结点归入合并后的链表中，否则，将head2指向的结点归入合并后的链表中。如果有一个链表遍历结束，则把未结束的链表连接到合并后的链表尾部。

下图以一个简单的示例为例介绍合并的具体方法：

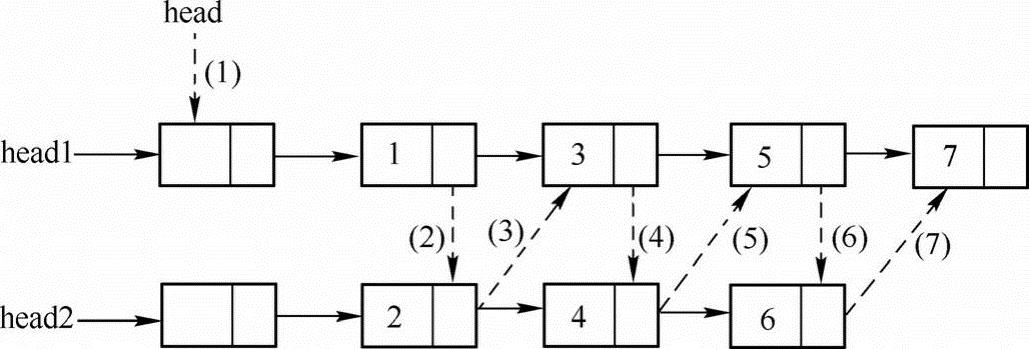
由于链表按升序排列，首先通过比较链表第一个结点中元素的大小来确定最终合并后链表的头结点；接下来每次都找两个链表中剩余结点的最小值链接到被合并的链表后面，如上图中的虚线所示。在实现的时候需要注意，要释放head2链表的头结点，具体实现代码如下：

程序的运行结果如下：

head1：1 3 5

head2：2 4 6

合并后的链表：1 2 3 4 5 6

算法性能分析：

以上这种方法只需要对链表进行一次遍历，因此，时间复杂度为O（n）。另外由于只需要几个指针变量来保存结点的地址信息，因此，空间复杂度为O（1）。

1.10 如何在只给定单链表中某个结点的指针的情况下删除该结点

【出自XM笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

假设给定链表1-＞2-＞3-＞4-＞5-＞6-＞7中指向第5个元素的指针，要求把结点5删掉，删除后链表变为1-＞2-＞3-＞4-＞6-＞7。

分析与解答：

一般而言，要删除单链表中的一个结点p，首先需要找到结点p的前驱结点pre，然后通过pre.next=p.next来实现对结点p的删除。对于本题而言，由于无法获取到结点p的前驱结点，因此，不能采用这种传统的方法。

那么如何解决这个问题呢？可以分如下两种情况来分析：

（1）如果这个结点是链表的最后一个结点，那么无法删除这个结点。

（2）如果这个结点不是链表的最后一个结点，可以通过把其后继结点的数据复制到当前结点中，然后删除后继结点的方法来实现。实现方法如下图所示：

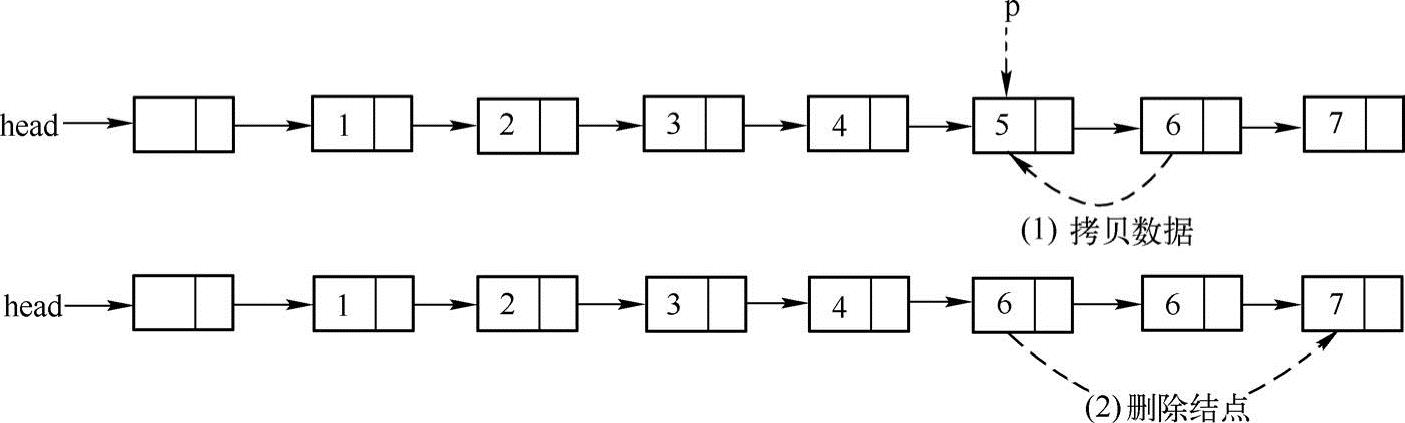
在上图中，第（1）步把结点p的后继结点的数据复制到结点p的数据域中；第（2）步把结点p的后继结点删除。实现代码如下：

程序的运行结果如下：

删除结点5前链表：1 2 3 4 5 6 7

删除该结点后链表：1 2 3 4 6 7

算法性能分析：

由于这种方法不需要遍历链表，只需要完成一个数据复制与结点删除的操作，因此，时间复杂度为O（1）。由于这种方法只用了常数个额外指针变量，因此，空间复杂度也为O（1）。

引申：只给定单链表中某个结点p（非空结点），如何在p前面插入一个结点

分析与解答：

主要思路：首先分配一个新结点q，把结点q插入在结点p后，然后把p的数据域复制到结点q的数据域中，最后把结点p的数据域设置为待插入的值。

1.11 如何判断两个单链表（无环）是否交叉

【出自WR笔试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

单链表相交指的是两个链表存在完全重合的部分，如下图所示：

在上图中，这两个链表相交于结点5，要求判断两个链表是否相交。如果相交，找出相交处的结点。

分析与解答：

方法一：Hash法

如上图所示，如果两个链表相交，那么它们一定会有公共的结点，由于结点的地址或引用可以作为结点的唯一标识，因此，可以通过判断两个链表中的结点是否有相同的地址或引用来判断链表是否相交。具体可以采用如下方法实现：首先遍历链表head1，把遍历到的所有结点的地址存放到HashSet中；接着遍历链表head2，每遍历到一个结点，就判断这个结点的地址在HashSet中是否存在，如果存在，那么说明两个链表相交并且当前遍历到的结点就是它们的相交点，否则直接将链表head2遍历结束，说明这两个单链表不相交。

算法性能分析：

由于这种方法需要分别遍历两个链表，因此，算法的时间复杂度为O（n1+n2），其中，n1与n2分别为两个链表的长度。此外，由于需要申请额外的存储空间来存储链表head1中结点的地址，因此，算法的空间复杂度为O（n1）。

方法二：首尾相接法

主要思路：将这两个链表首尾相连（例如把链表head1尾结点链接到head2的头指针），然后检测这个链表是否存在环，如果存在，则两个链表相交，而环入口结点即为相交的结点，如下图所示。具体实现方法以及算法性能分析见1.6节。

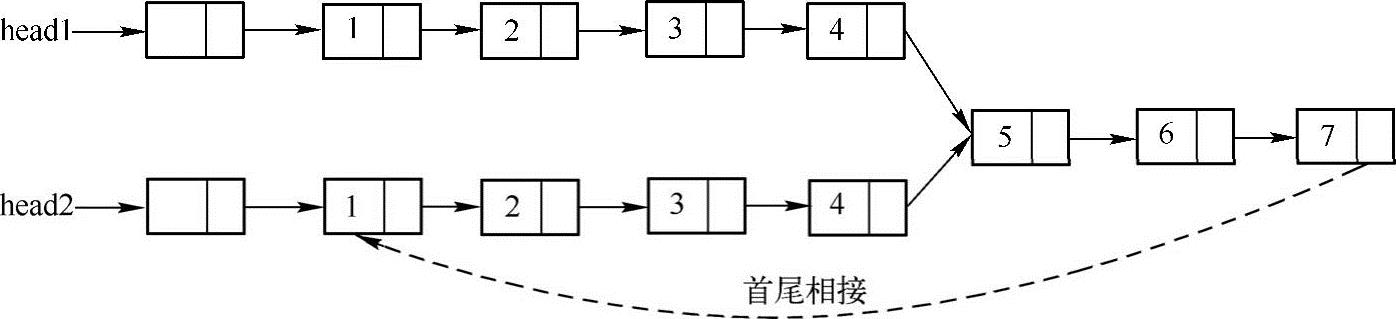
方法三：尾结点法

主要思路：如果两个链表相交，那么两个链表从相交点到链表结束都是相同的结点，必然是Y字形（如上图所示），所以，判断两个链表的最后一个结点是不是相同即可。即先遍历一个链表，直到尾部，再遍历另外一个链表，如果也可以走到同样的结尾点，则两个链表相交，这时记下两个链表的长度n1、n2，再遍历一次，长链表结点先出发前进|n1-n2|步，之后两个链表同时前进，每次一步，相遇的第一点即为两个链表相交的第一个点。实现代码如下：

程序运行结果为

这两个链表相交点为5

运行结果分析：

在上述代码中，由于构造的两个单链表相交于结点5，因此，输出结果中它们的相交结点为5。

算法性能分析：

假设这两个链表长度分别为n1，n2，重叠的结点的个数为L（0＜L＜min（n1，n2）），则总共对链表进行遍历的次数为n1+n2+L+n1-L+n2-L=2（n1+n2）-L，因此，算法的时间复杂度为O（n1+n2）；由于这种方法只使用了常数个额外指针变量，因此，空间复杂度为O（1）。

引申：如果单链表有环，如何判断两个链表是否相交

分析与解答：

（1）如果一个单链表有环，另外一个没环，那么它们肯定不相交。

（2）如果两个单链表都有环并且相交，那么这两个链表一定共享这个环。判断两个有环的链表是否相交的方法：首先采用本章第1.6节中介绍的方法找到链表head1中环的入口点p1，然后遍历链表head2，判断链表中是否包含结点p1，如果包含，则这两个链表相交，否则不相交。找相交点的方法：把结点p1看作两个链表的尾结点，这样就可以把问题转换为求两个无环链表相交点的问题，可以采用本节介绍的求相交点的方法来解决这个问题。

1.12 如何展开链接列表

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个有序链表，其中每个结点也表示一个有序链表，结点包含两个类型的指针：

（1）指向主链表中下一个结点的指针（在下面的代码中称为“正确”指针）。

（2）指向此结点头的链表（在下面的代码中称之为“down”指针）。

所有链表都被排序。请参见以下示例：

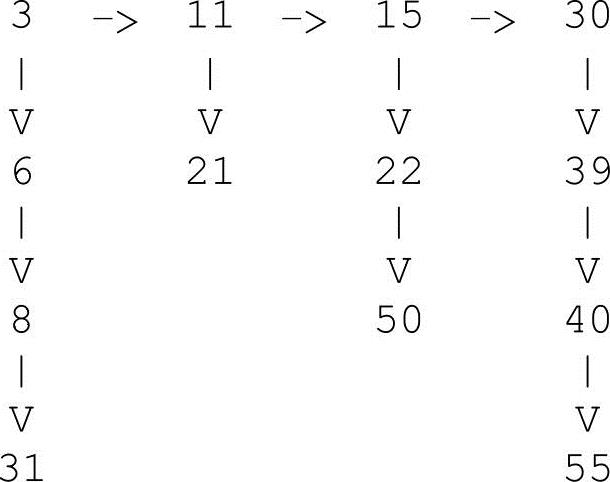
实现一个函数flatten（），该函数用来将链表扁平化成单个链表，扁平化的链表也应该被排序。例如，对于上述输入链表，输出链表应为3-＞6-＞8-＞11-＞15-＞21-＞22-＞30-＞31-＞39-＞40-＞45-＞50。

分析与解答：

本题的主要思路为使用归并排序中的合并操作，使用归并的方法把这些链表来逐个归并。具体而言，可以使用递归的方法，递归地合并已经扁平化的链表与当前的链表。在实现的过程可以使用down指针来存储扁平化处理后的链表。实现代码如下：

程序运行结果如下：

3 6 8 11 15 21 22 30 31 39 40 50 55

第2章 栈、队列与哈希

栈与队列是在程序设计中被广泛使用的两种重要的线性数据结构，都是在一个特定范围的存储单元中存储的数据，这些数据都可以重新被取出使用，与线性表相比，它们的插入和删除操作受到更多的约束和限定，故又称为限定性的线性表结构。不同的是，栈就像一个很窄的桶，先存进去的数据只能最后被取出来，是LIFO（LastInFirstOut，后进先出），它将进出顺序逆序，即先进后出，后进先出，栈结构如图2-1所示。队列像日常排队买东西的人的“队列”，先排队的人先买，后排队的人后买，是FIFO（FirstInFirstOut，先进先出），它保持进出顺序一致，即先进先出，后进后出，队列结构如图2-2所示。

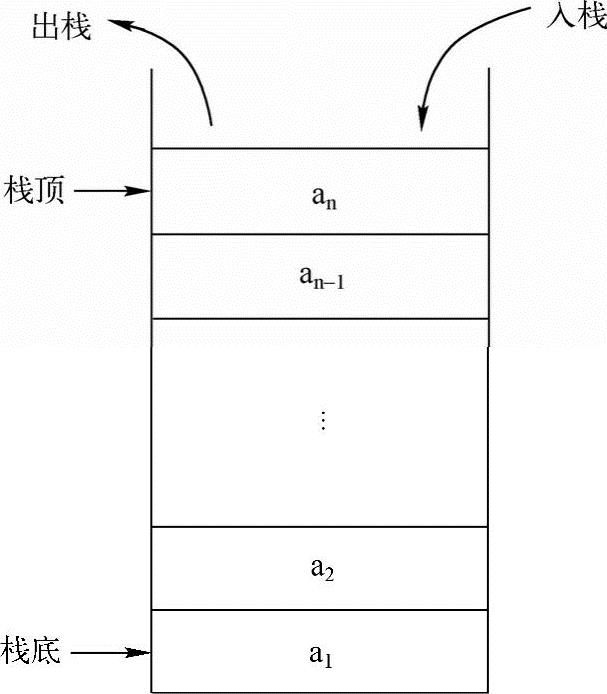
图2-1 栈结构示意图

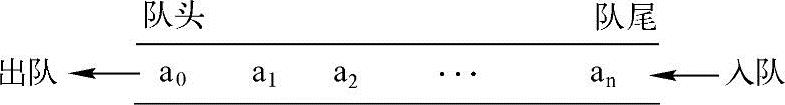
图2-2 队列结构示意图

需要注意的是，有时在数据结构中还有可能出现按照大小排队或按照一定条件排队的数据队列，这时的队列属于特殊队列，就不一定按照“先进先出”的原则读取数据了。

2.1 如何实现栈

【出自ALBB面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

实现一个栈的数据结构，使其具有以下方法：压栈、弹栈、取栈顶元素、判断栈是否为空以及获取栈中元素个数。

分析与解答：

栈的实现有两种方法，分别为采用数组来实现和采用链表来实现。下面分别详细介绍这两种方法。

方法一：数组实现

在采用数组来实现栈的时候，栈空间是一段连续的空间。实现思路如下图所示：

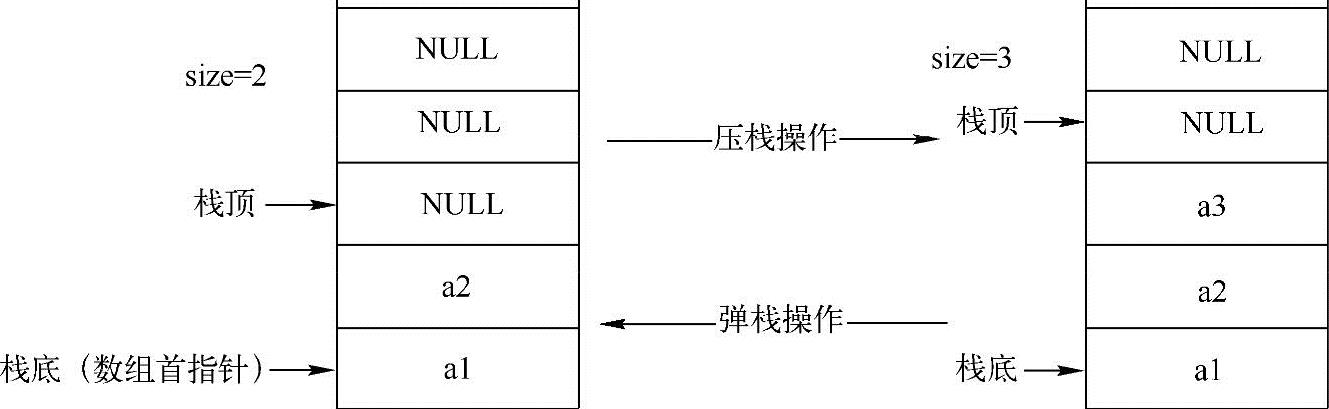
从上图中可以看出，可以把数组的首元素当作栈底，同时记录栈中元素的个数size，假设数组首地址为arr，从上图可以看出，压栈的操作其实是把待压栈的元素放到数组arr[size]中，然后执行size++操作；同理，弹栈操作其实是取数组arr[size-1]元素，然后执行size--操作。根据这个原理可以非常容易实现栈，示例代码如下：

方法二：链表实现

在创建链表的时候经常采用一种从头结点插入新结点的方法，可以采用这种方法来实现栈，最好使用带头结点的链表，这样可以保证对每个结点的操作都是相同的，实现思路如下图所示：

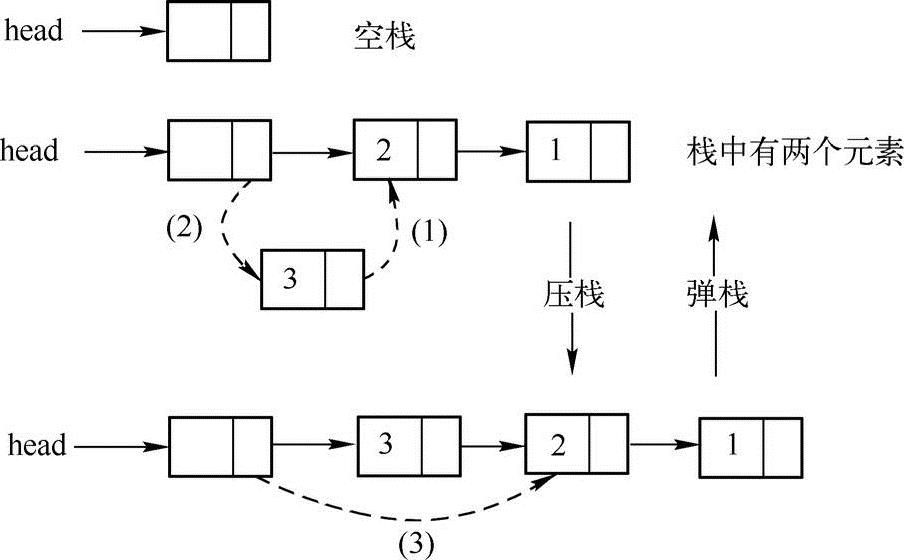
在上图中，在进行压栈操作的时候，首先需要创建新的结点，把待压栈的元素放到新结点的数据域中，然后只需要（1）和（2）两步就实现了压栈操作（把新结点加到了链表首部）。同理，在弹栈的时候，只需要进行（3）的操作就可以删除链表的第一个元素，从而实现弹栈操作。实现代码如下：

程序的运行结果如下：

栈顶元素为：1

栈大小为：1

弹栈成功

栈已经为空

两种方法的对比

采用数组实现栈的优点是：一个元素值占用一个存储空间；缺点是：如果初始化申请的存储空间太大，会造成空间的浪费；如果申请的存储空间太小，后期会经常需要扩充存储空间，扩充存储空间是个费时的操作，这样会造成性能的下降。

采用链表实现栈的优点是：使用灵活方便，只有在需要的时候才会申请空间。缺点是：除了要存储元素外，还需要额外的存储空间存储指针信息。

算法性能分析：

这两种方法压栈与弹栈的时间复杂度都为O（1）。

2.2 如何实现队列

【出自XL面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

实现一个队列的数据结构，使其具有入队列、出队列、查看队列首尾元素及查看队列大小等功能。

分析与解答：

与实现栈的方法类似，队列的实现也有两种方法，分别为采用数组来实现和采用链表来实现。下面分别详细介绍这两种方法。

方法一：数组实现

下图给出了一种最简单的实现方式，用front来记录队列首元素的位置，用rear来记录队列尾元素往后一个位置。入队列的时候只需要将待入队列的元素放到数组下标为rear的位置，同时执行rear++，出队列的时候只需要执行front++即可。

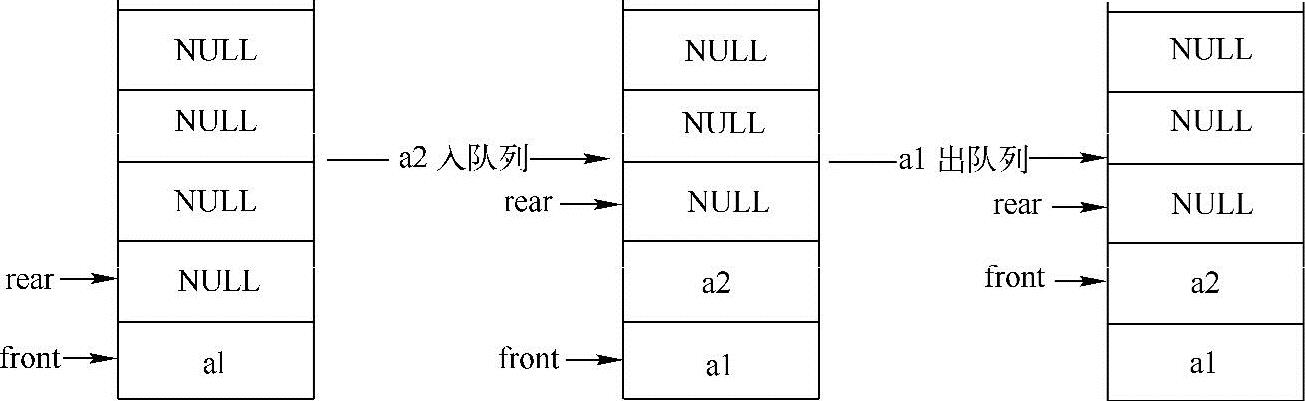
示例代码如下：

程序的运行结果如下：

队列头元素为：1

队列尾元素为：2

队列大小为：2

以上这种实现方法最大的缺点是：出队列后数组前半部分的空间不能够充分地利用，解决这个问题的方法是把数组看成一个环状的空间（循环队列）。当数组最后一个位置被占用后，可以从数组首位置开始循环利用，具体实现方法可以参考数据结构的课本。

方法二：链表实现

采用链表实现队列的方法与实现栈的方法类似，分别用两个指针指向队列的首元素与尾元素，如下图所示。用pHead来指向队列的首元素，用pEnd来指向队列的尾元素。

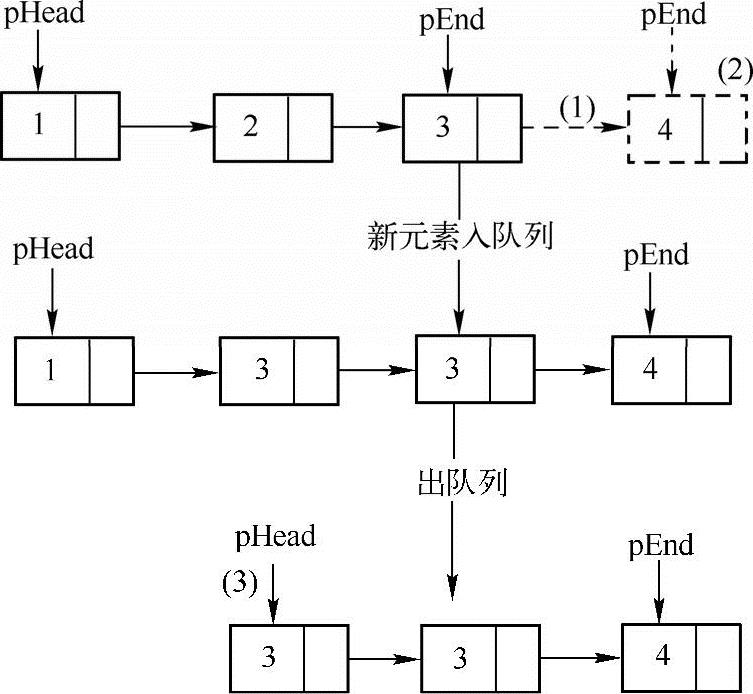
在上图中，刚开始队列中只有元素1、2和3，当新元素4要进队列的时候，只需要上图中（1）和（2）两步，就可以把新结点连接到链表的尾部，同时修改pEnd指针指向新增加的结点。出队列的时候只需要（3）一步，改变pHead指针使其指向pHead-＞next，此外也需要考虑结点所占空间释放的问题。在入队列与出队列的操作中也需要考虑队列尾空的时候的特殊操作，实现代码如下：

程序的运行结果如下：

队列头元素为：1

队列尾元素为：2

队列大小为：2

显然用链表来实现队列有更好的灵活性，与数组的实现方法相比，它多了用来存储结点关系的指针空间。此外，也可以用循环链表来实现队列，这样只需要一个指向链表最后一个元素的指针即可，因为通过指向链表尾元素可以非常容易地找到链表的首结点。

2.3 如何翻转栈的所有元素

【出自ALBB面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

翻转（也叫颠倒）栈的所有元素，例如输入栈{1，2，3，4，5}，其中，1处在栈顶，翻转之后的栈为{5，4，3，2，1}，其中，5处在栈顶。

分析与解答：

最容易想到的办法是申请一个额外的队列，先把栈中的元素依次出栈放到队列里，然后把队列里的元素按照出队列顺序入栈，这样就可以实现栈的翻转，这种方法的缺点是需要申请额外的空间存储队列，因此，空间复杂度较高。下面介绍一种空间复杂度较低的递归的方法。

递归程序有两个关键因素需要注意：递归定义和递归终止条件。经过分析后，很容易得到该问题的递归定义和递归终止条件。递归定义：将当前栈的最底元素移到栈顶，其他元素顺次下移一位，然后对不包含栈顶元素的子栈进行同样的操作。终止条件：递归下去，直到栈为空。递归的调用过程如下图所示：

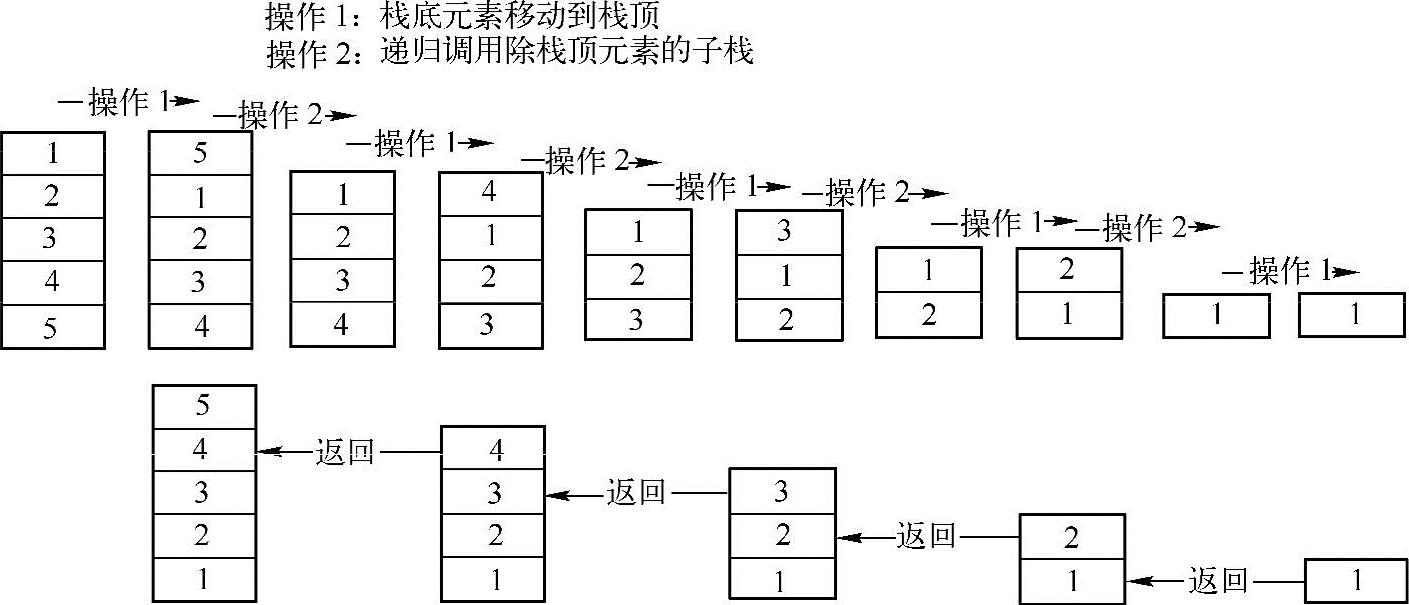
在上图中，对于栈{1，2，3，4，5}，进行翻转的操作是：首先把栈底元素移动到栈顶得到栈{5，1，2，3，4}，然后对不包含栈顶元素的子栈进行递归调用（对子栈元素进行翻转），子栈{1，2，3，4}翻转的结果为{4，3，2，1}，因此，最终得到翻转后的栈为{5，4，3，2，1}。

此外，由于栈的后进先出的特点，使得只能取栈顶的元素，因此，要把栈底的元素移动到栈顶也需要递归调用才能完成，主要思路：把不包含该栈顶元素的子栈的栈底的元素移动到子栈的栈顶，然后把栈顶的元素与子栈栈顶的元素（其实就是与栈顶相邻的元素）进行交换。

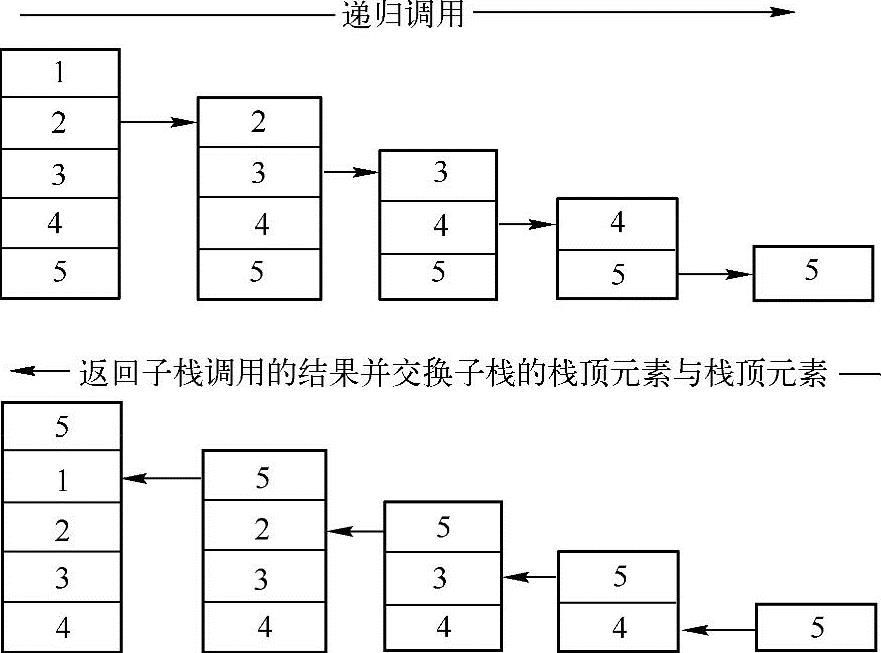
为了更容易理解递归调用，可以认为在进行递归调用的时候，子栈已经把栈底元素移动到了栈顶，在上图中，为了把栈{1，2，3，4，5}的栈底元素5移动到栈顶，首先对子栈{2，3，4，5}进行递归调用，调用的结果为{5，2，3，4}，然后对子栈顶元素5，与栈顶元素1进行交换得到栈{5，1，2，3，4}，实现了把栈底元素移动到栈顶。

实现代码如下：

程序的运行结果如下：

翻转后出栈顺序为：5 4 3 2 1

算法性能分析：

把栈底元素移动到栈顶操作的时间复杂度为O（N），在翻转操作中对每个子栈都进行了把栈底元素移动到栈顶的操作，因此，翻转算法的时间复杂度为O（N^2）。

引申：如何给栈排序

分析与解答：

很容易通过对上述方法进行修改得到栈的排序算法。主要思路：首先对不包含栈顶元素的子栈进行排序，如果栈顶元素大于子栈的栈顶元素，则交换这两个元素。因此，在上述方法中，只需要在交换栈顶元素与子栈顶元素的时候增加一个条件判断即可实现栈的排序，实现代码如下：

程序的运行结果如下：

排后出栈顺序为：1 2 3

算法性能分析：

这种方法的时间复杂度为O（N^2）。

2.4 如何根据入栈序列判断可能的出栈序列

【出自TX面试题】

难度系数：★★★☆☆ 被考察系数：★★★★★

题目描述：

输入两个整数序列，其中一个序列表示栈的push（入）顺序，判断另一个序列有没有可能是对应的pop（出）顺序。

分析与解答：

假如输入的push序列是1、2、3、4、5，那么3、2、5、4、1就有可能是一个pop序列，但5、3、4、1、2就不可能是它的一个pop序列。

主要思路是使用一个栈来模拟入栈顺序，具体步骤如下：

（1）把push序列依次入栈，直到栈顶元素等于pop序列的第一个元素，然后栈顶元素出栈，pop序列移动到第二个元素。

（2）如果栈顶继续等于pop序列现在的元素，则继续出栈并pop后移；否则对push序列继续入栈。

（3）如果push序列已经全部入栈，但是pop序列未全部遍历，而且栈顶元素不等于当前pop元素，那么这个序列不是一个可能的出栈序列。如果栈为空，而且pop序列也全部被遍历过，则说明这是一个可能的pop序列。下图给出一个合理的pop序列的判断过程。

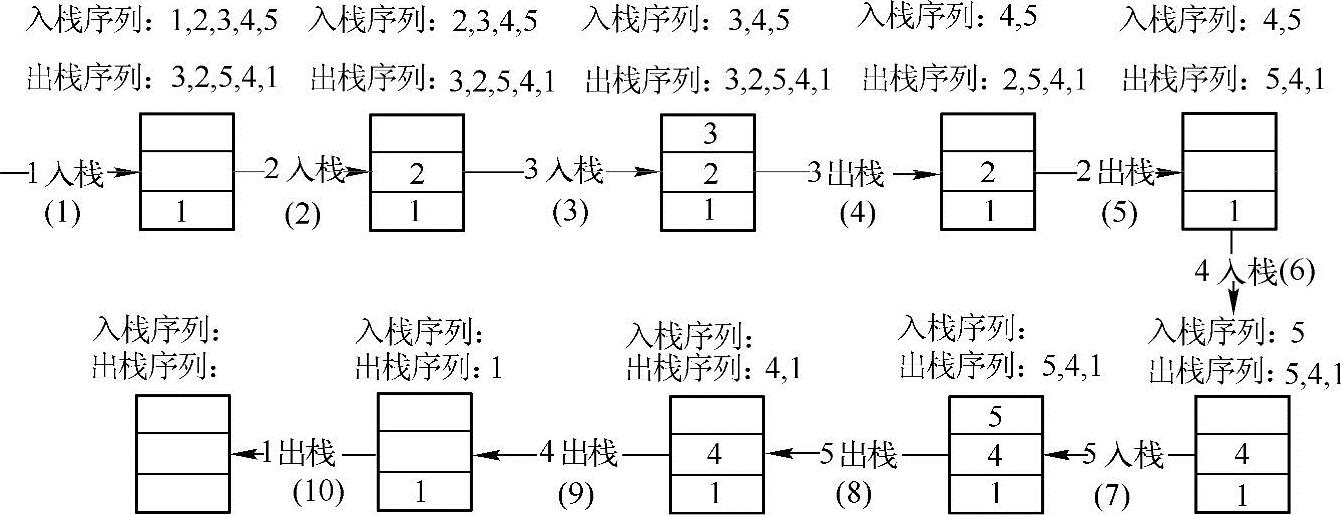
在上图中，（1）～（3）三步，由于栈顶元素不等于pop序列第一个元素3，因此，1，2，3依次入栈，当3入栈后，栈顶元素等于pop序列的第一个元素3，因此，第（4）步执行3出栈，接下来指向第二个pop序列2，且栈顶元素等于pop序列的当前元素，因此，第（5）步执行2出栈；接着由于栈顶元素4不等于当前pop序列5，因此，接下来（6）和（7）两步分别执行4和5入栈；接着由于栈顶元素5等于pop序列的当前值，因此，第（8）步执行5出栈，接下来（9）和（10）两步栈顶元素都等于当前pop序列的元素，因此，都执行出栈操作。最后由于栈为空，同时pop序列都完成了遍历，因此，{3，2，5，4，1}是一个合理的出栈序列。

实现代码如下：

程序的运行结果如下：

32541是12345的一个pop序列

算法性能分析：

这种方法在处理一个合理的pop序列的时候需要操作的次数最多，即把push序列进行一次压栈和出栈操作，操作次数为2N，因此，时间复杂度为O（N），此外，这种方法使用了额外的栈空间，因此，空间复杂度为O（N）。

2.5 如何用O（1）的时间复杂度求栈中最小元素

【出自XM面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

分析与解答：

由于栈具有后进先出的特点，因此，push和pop只需要对栈顶元素进行操作。如果使用上述的实现方式，只能访问到栈顶的元素，无法得到栈中最小的元素。当然，可以用另外一个变量来记录栈底的位置，通过遍历栈中所有的元素找出最小值，但是这种方法的时间复杂度为O（N），那么如何才能用O（1）的时间复杂度求出栈中最小的元素呢？

在算法设计中，经常会采用空间换取时间的方式来提高时间复杂度，也就是说采用额外的存储空间来降低操作的时间复杂度。具体而言，在实现的时候使用两个栈结构，一个栈用来存储数据，另外一个栈用来存储栈的最小元素。实现思路如下：如果当前入栈的元素比原来栈中的最小值还小，则把这个值压入保存最小元素的栈中；在出栈的时候，如果当前出栈的元素恰好为当前栈中的最小值，保存最小值的栈顶元素也出栈，使得当前最小值变为当前最小值入栈之前的那个最小值。为了简单起见，可以在栈中保存int类型。

实现代码如下：

程序的运行结果如下：

栈中最小值为：5

栈中最小值为：5

栈中最小值为：2

栈中最小值为：5

算法性能分析：

这种方法申请了额外的一个栈空间来保存栈中最小的元素，从而达到了用O（1）的时间复杂度求栈中最小元素的目的，但是付出的代价是空间复杂度为O（N）。

2.6 如何用两个栈模拟队列操作

【出自JD面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

分析与解答：

题目要求用两个栈来模拟队列，假设使用栈A与栈B模拟队列Q，A为插入栈，B为弹出栈，以实现队列Q。

再假设A和B都为空，可以认为栈A提供入队列的功能，栈B提供出队列的功能。

要入队列，入栈A即可，而出队列则需要分两种情况考虑：

（1）如果栈B不为空，则直接弹出栈B的数据。

（2）如果栈B为空，则依次弹出栈A的数据，放入栈B中，再弹出栈B的数据。

实现代码如下：

程序的运行结果为

队列首元素为：1

队列首元素为：2

算法性能分析：

这种方法入队操作的时间复杂度为O（1），出队列操作的时间复杂度则依赖于入队与出队执行的频率。总体来讲，出队列操作的时间复杂度为O（1），当然会有个别操作需要耗费更多的时间（因为需要从两个栈之间移动数据）。

2.7 如何设计一个排序系统

【出自TX笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

请设计一个排队系统，能够让每个进入队伍的用户都能看到自己在队列中所处的位置和变化，队伍可能随时有人加入和退出；当有人退出影响到用户的位置排名时需要及时反馈到用户。

分析与解答：

本题不仅要实现队列常见的入队列与出队列的功能，而且还需要实现队列中任意一个元素都可以随时出队列，且出队列后需要更新队列用户位置的变化。实现代码如下：

程序的运行结果如下：

User（id=2，name=user2，seq=1）

User（id=4，name=user4，seq=2）

2.8 如何实现LRU缓存方案

【出自MT面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述

LRU是Least Recently Used的缩写，它的意思是“最近最少使用”，LRU缓存就是使用这种原理实现，简单地说就是缓存一定量的数据，当超过设定的阈值时就把一些过期的数据删除掉。常用于页面置换算法，是虚拟页式存储管理中常用的算法。如何实现LRU缓存方案？

分析与解答：

可以使用两个数据结构实现一个LRU缓存。

（1）使用双向链表实现的队列，队列的最大容量为缓存的大小。在使用过程中，把最近使用的页面移动到队列头，最近没有使用的页面将被放在队列尾的位置。

（2）使用一个哈希表，把页号作为键，把缓存在队列中的结点的地址作为值。

当引用一个页面时，所需的页面在内存中，需要把这个页对应的结点移动到队列的前面。如果所需的页面不在内存中，我们将它存储在内存中。简单地说，就是将一个新结点添加到队列的前面，并在哈希表中更新相应的结点地址。如果队列是满的，那么就从队列尾部移除一个结点，并将新结点添加到队列的前面。实现代码如下：

程序运行结果为

7 6 1

2.9 如何从给定的车票中找出旅程

【出自YMX面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一趟旅途旅程中所有的车票信息，根据这个车票信息找出这趟旅程的路线。例如：给定下面的车票：（“西安”到“成都”），（“北京”到“上海”），（“大连”到“西安”），（“上海”到“大连”）。那么可以得到旅程路线为：北京-＞上海，上海-＞大连，大连-＞西安，西安-＞成都。假定给定的车票不会有环，也就是说有一个城市只作为终点而不会作为起点。

分析与解答：

对于这种题目，一般而言可以使用拓扑排序进行解答。根据车票信息构建一个图，然后找出这张图的拓扑排序序列，这个序列就是旅程的路线。但这种方法的效率不高，它的时间复杂度为O（N）。这里重点介绍另外一种更加简单的方法：hash法。主要的思路为根据车票信息构建一个HashMap，然后从这个HashMap中找到整个旅程的起点，接着就可以从起点出发依次找到下一站，进而知道终点。具体的实现思路如下：

（1）根据车票的出发地与目的地构建HashMap。

Tickets={（“西安”到“成都”），（“北京”到“上海”），（“大连”到“西安”），（“上海”到“大连”）}

（2）构建Tickets的逆向hashmap如下（将旅程的起始点反向）：

ReverseTickets={（“成都”到“西安”），（“上海”到“北京”），（“西安”到“大连”），（“大连”到“上海”）}

（3）遍历Tickets，对于遍历到的key值，判断这个值是否在ReverseTickets中的key中存在，如果不存在，那么说明遍历到的Tickets中的key值就是旅途的起点。例如：“北京”在ReverseTickets的key中不存在，因此“北京”就是旅途的起点。实现代码如下：

程序的运行结果如下：

北京-＞上海，北京-＞大连，大连-＞西安，西安-＞成都

算法性能分析：

这种方法的时间复杂度为O（N），空间复杂度也为O（N）。

2.10 如何从数组中找出满足a+b=c+d的两个数对

【出自YMX面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个数组，找出数组中是否有两个数对（a，b）和（c，d），使得a+b=c+d，其中，a、b、c和d是不同的元素。如果有多个答案，打印任意一个即可。例如给定数组：{3，4，7，10，20，9，8}，可以找到两个数对（3，8）和（4，7），使得3+8=4+7。

分析与解答：

最简单的方法就是使用四重遍历，对所有可能的数对，判断是否满足题目要求，如果满足则打印出来，但是这种方法的时间复杂度为O（N^4），很显然不满足要求。下面介绍另外一种方法——hash法，算法的主要思路是：以数对为单位进行遍历，在遍历过程中，把数对和数对的值存储在哈希表中（键为数对的和，值为数对），当遍历到一个键值对，如果它的和在哈希表中已经存在，那么就找到了满足条件的键值对。下面以HashMap为例给出实现代码：

程序的运行结果如下：

（3，8），（4，7）

算法性能分析：

这种方法的时间复杂度为O（n^2）。因为使用了双重循环，而HashMap的插入与查找操作实际的时间复杂度为O（1）。

第3章 二叉树

3.1 二叉树基础知识

二叉树（Binary Tree）也称为二分树、二元树、对分树等，它是n（n≥0）个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，称该二叉树为空二叉树。

在二叉树中，一个元素也称作一个结点。二叉树的递归定义是：二叉树或者是一棵空树，或者是一棵由一个根结点和两棵互不相交的分别称作根结点的左子树和右子树所组成的非空树，左子树和右子树又同样都是一棵二叉树。

以下是一些常见的二叉树的基本概念：

（1）结点的度。结点所拥有的子树的个数称为该结点的度。

（2）叶子结点。度为0的结点称为叶子结点，或者称为终端结点。

（3）分支结点。度不为0的结点称为分支结点，或者称为非终端结点。一棵树的结点除叶子结点外，其余的都是分支结点。

（4）左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。

（5）路径、路径长度。如果一棵树的一串结点n1，n2，…，nk有如下关系：结点ni是ni+1的父结点（1≤i＜k），就把n1，n2，…，nk称为一条由n1至nk的路径。这条路径的长度是k-1。

（6）祖先、子孙。在树中，如果有一条路径从结点M到结点N，那么M就称为N的祖先，而N称为M的子孙。

（7）结点的层数。规定树的根结点的层数为1，其余结点的层数等于它的双亲结点的层数加1。

（8）树的深度。树中所有结点的最大层数称为树的深度。

（9）树的度。树中各结点度的最大值称为该树的度，叶子结点的度为0。

（10）满二叉树。在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的一棵二叉树称作满二叉树。

（11）完全二叉树。一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

二叉树的基本性质如下所示：

性质1：一棵非空二叉树的第i层上最多有2^i-1个结点（i≥1）。

性质2：一棵深度为k的二叉树中，最多具有2^k-1个结点，最少有k个结点。

性质3：对于一棵非空的二叉树，度为0的结点（即叶子结点）总是比度为2的结点多一个，即如果叶子结点数为n0，度数为2的结点数为n2，则有n0=n2+1。

证明：用n0表示度为0（叶子结点）的结点总数，用n1表示度为1的结点总数，n2表示度为2的结点总数，n表示整个完全二叉树的结点总数。则n=n0+n1+n2，根据二叉树和树的性质，可知n=n1+2*n2+1（所有结点的度数之和+1=结点总数），根据两个等式可知n0+n1+n2=n1+2*n2+1，所以，n2=n0-1，即n0=n2+1。所以，答案为1。

性质4：具有n个结点的完全二叉树的深度为log₂n」+1。

证明：根据性质2，深度为k的二叉树最多只有2^k-1个结点，且完全二叉树的定义是与同深度的满二叉树前面编号相同，即它的总结点数n位于k层和k-1层满二叉树容量之间，即2^k-1_-1＜n≤2^k-1或2^k-1≤n＜2^k，三边同时取对数，于是有k-1≤log₂n＜k，因为k是整数，所以，k=log₂n」+1。

性质5：对于具有n个结点的完全二叉树，如果按照从上至下和从左到右的顺序对二叉树中的所有结点从1开始顺序编号，则对于任意的序号为i的结点，有：（1）如果i＞1，则序号为i的结点的双亲结点的序号为i/2（其中“/”表示整除）；如果i=1，则序号为i的结点是根结点，无双亲结点。（2）如果2i≤n，则序号为i的结点的左孩子结点的序号为2i；如果2i＞n，则序号为i的结点无左孩子。（3）如果2i+1≤n，则序号为i的结点的右孩子结点的序号为2i+1；如果2i+1＞n，则序号为i的结点无右孩子。

此外，若对二叉树的根结点从0开始编号，则相应的i号结点的双亲结点的编号为（i-1）/2，左孩子的编号为2i+1，右孩子的编号为2i+2。

例题1：一棵完全二叉树上有1001个结点，其中叶子结点的个数是多少？

分析：二叉树的公式：n=n0+n1+n2=n0+n1+（n0-1）=2*n0+n1-1。而在完全二叉树中，n1只能取0或1。若n1=1，则2*n0=1001，可推出n0为小数，不符合题意；若n1=0，则2*n0-1=1001，则n0=501。所以，答案为501。

例题2：如果根的层次为1，具有61个结点的完全二叉树的高度为多少？

分析：根据二叉树的性质，具有n个结点的完全二叉树的深度为+1，因此，含有61个结点的完全二叉树的高度为+1，即应该为6层。所以，答案为6。

例题3：在具有100个结点的树中，其边的数目为多少？

分析：在一棵树中，除了根结点之外，每一个结点都有一条入边，因此，总边数应该是100-1，即99条。所以，答案为99。

二叉树有顺序存储和链式存储两种存储结构，本章涉及的算法都采用的是链式存储结构，本章示例代码用到的二叉树的结构如下：

3.2 如何把一个有序整数数组放到二叉树中

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

分析与解答：

如果要把一个有序的整数数组放到二叉树中，那么所构造出来的二叉树必定也是一棵有序的二叉树。鉴于此，实现思路是：取数组的中间元素作为根结点，将数组分成左右两部分，对数组的两部分用递归的方法分别构建左右子树。如下图所示：

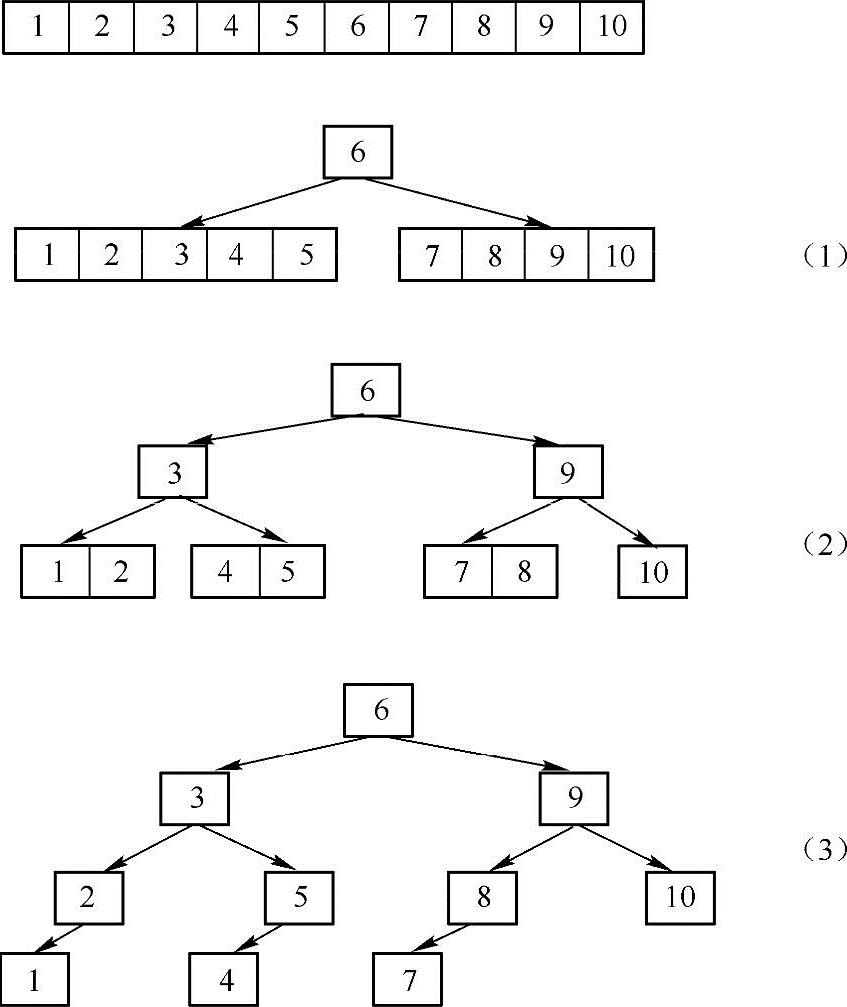
如上图所示，首先取数组的中间结点6作为二叉树的根结点，把数组分成左右两部分，然后对于数组的左右两部分子数组分别运用同样的方法进行二叉树的构建，例如，对于左半部分子数组，取中间结点3作为树的根结点，再把孩子数组分成左右两部分。依此类推，就可以完成二叉树的构建，实现代码如下：

程序的运行结果如下：

数组：1 2 3 4 5 6 7 8 9 1 0

转换成树的中序遍历为：1 2 3 4 5 6 7 8 9 1 0

算法性能分析：

由于这种方法只遍历了一次数组，因此，算法的时间复杂度为O（N），其中，N表示的是数组长度。

3.3 如何从顶部开始逐层打印二叉树结点数据

【出自WR面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一棵二叉树，要求逐层打印二叉树结点的数据，例如有如下二叉树：

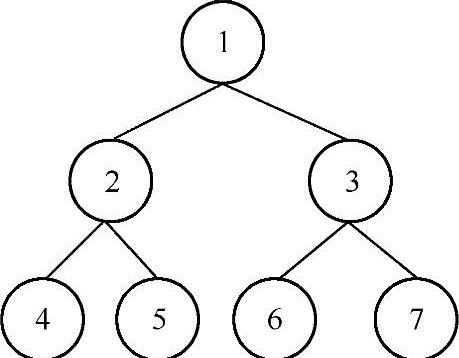
对这棵二叉树层序遍历的结果为1，2，3，4，5，6，7。

分析与解答：

为了实现对二叉树的层序遍历，就要求在遍历一个结点的同时记录下它的孩子结点的信息，然后按照这个记录的顺序来访问结点的数据，在实现的时候可以采用队列来存储当前遍历到的结点的孩子结点，从而实现二叉树的层序遍历，遍历过程如下图所示：

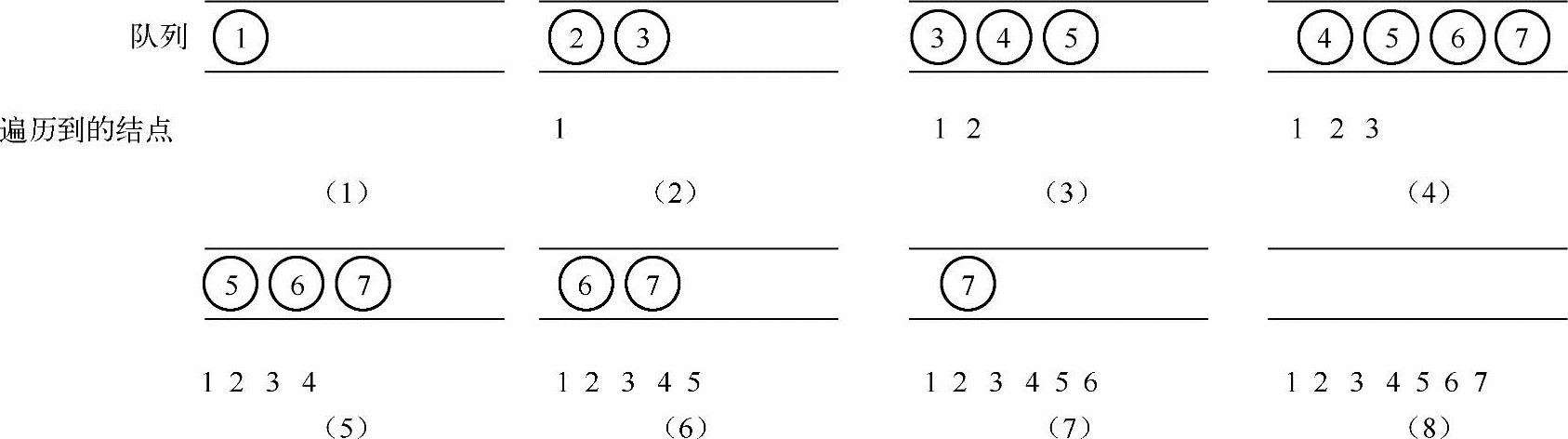
在上图中，图（1）首先把根结点1放到队列里面，然后开始遍历。图（2）队列首元素（结点1）出队列，同时它的孩子结点2和结点3进队列。图（3）接着出队列的结点为2，同时把它的孩子结点4和结点5放到队列里，依此类推就可以实现对二叉树的层序遍历。

实现代码如下：

测试数据采用了3.2节所构造的数，程序的运行结果如下：

树的层序遍历结果为：6 3 9 2 5 8 10 1 4 7

算法性能分析：

在二叉树的层序遍历过程中，对树中的各个结点只进行了一次访问，因此，时间复杂度为O（N），此外，这种方法还使用了队列来保存遍历的中间结点，所使用队列的大小取决于二叉树中每一层中结点个数的最大值。具有N个结点的完全二叉树的深度为h=log₂N+1。而深度为h的这一层最多的结点个数为2^h-1=n/2。也就是说队列中可能的最多的结点个数为N/2。因此，这种算法的空间复杂度为O（N）。

引申：用空间复杂度为O（1）的算法来实现层序遍历

上面介绍的算法的空间复杂度为O（N），显然不满足要求。通常情况下，提高空间复杂度都是要以牺牲时间复杂度作为代价的。对于本题而言，主要的算法思路是：不使用队列来存储每一层遍历到的结点，而是每次都会从根结点开始遍历。把遍历二叉树的第k层的结点，转换为遍历二叉树根结点的左右子树的第k-1层结点。算法如下：

通过上述算法，可以首先求解出二叉树的高度h，然后调用上面的函数h次就可以打印出每一层的结点。

3.4 如何求一棵二叉树的最大子树和

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一棵二叉树，它的每个结点都是正整数或负整数，如何找到一棵子树，使得它所有结点的和最大？

分析与解答：

要求一棵二叉树的最大子树和，最容易想到的办法就是针对每棵子树，求出这棵子树中所有结点的和，然后从中找出最大值。恰好二叉树的后序遍历就能做到这一点。在对二叉树进行后序遍历的过程中，如果当前遍历的结点的值与其左右子树和的值相加的结果大于最大值，则更新最大值。如下图所示：

在上面这个图中，首先遍历结点-1，这个子树的最大值为-1，同理，当遍历到结点9时，子树的最大值为9，当遍历到结点3的时候，这个结点与其左右孩子结点值的和（3-1+9=11）大于最大值（9）。因此，此时最大的子树为以3为根结点的子树，依此类推直到遍历完整棵树为止。实现代码如下：

程序的运行结果如下：

最大子树和为：11

对应子树的根结点为：3

算法性能分析：

这种方法与二叉树的后序遍历有相同的时间复杂度，即为O（N），其中，N为二叉树的结点个数。

3.5 如何判断两棵二叉树是否相等

【出自BD面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

两棵二叉树相等是指这两棵二叉树有着相同的结构，并且在相同位置上的结点有相同的值。如何判断两棵二叉树是否相等？

分析与解答：

如果两棵二叉树root1、root2相等，那么root1与root2结点的值相同，同时它们的左右孩子也有着相同的结构，并且对应位置上结点的值相等，即root1.data==root2.data，并且root1的左子树与root2的左子树相等，root1的右子树与root2的右子树相等。根据这个条件，可以非常容易地写出判断两棵二叉树是否相等的递归算法。实现代码如下：

程序的运行结果如下：

这两棵树相等

算法性能分析：

这种方法对两棵树只进行了一次遍历，因此，时间复杂度为O（N）。此外，这种方法没有申请额外的存储空间。

3.6 如何把二叉树转换为双向链表

【出自XL笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

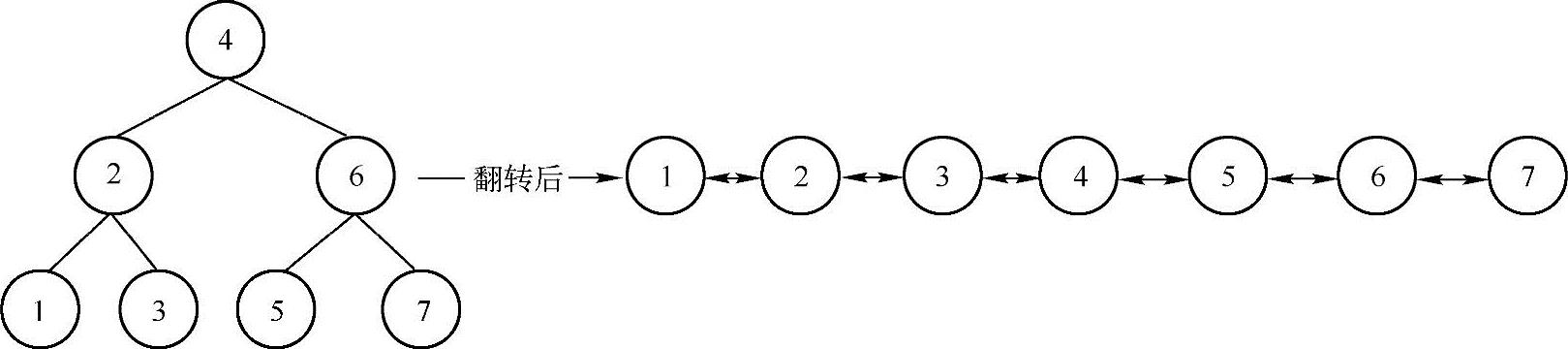
输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整结点的指向。例如：

分析与解答：

由于转换后的双向链表中结点的顺序与二叉树的中序遍历的顺序相同，因此，可以对二叉树的中序遍历算法进行修改，通过在中序遍历的过程中修改结点的指向来转换成一个排序的双向链表。实现思路如下图所示：假设当前遍历的结点为root，root的左子树已经被转换为双向链表（如下图（1）所示），使用两个变量pHead与pEnd分别指向链表的头结点与尾结点。那么在遍历root结点的时候，只需要将root结点的lchild（左）指向pEnd，把pEnd的rchild（右）指向root；此时root结点就被加入到双向链表里了，因此，root变成了双向链表的尾结点。对于所有的结点都可以通过同样的方法来修改结点的指向。因此，可以采用递归的方法来求解，在求解的时候需要特别注意递归的结束条件以及边界情况（例如双向链表为空的时候）。

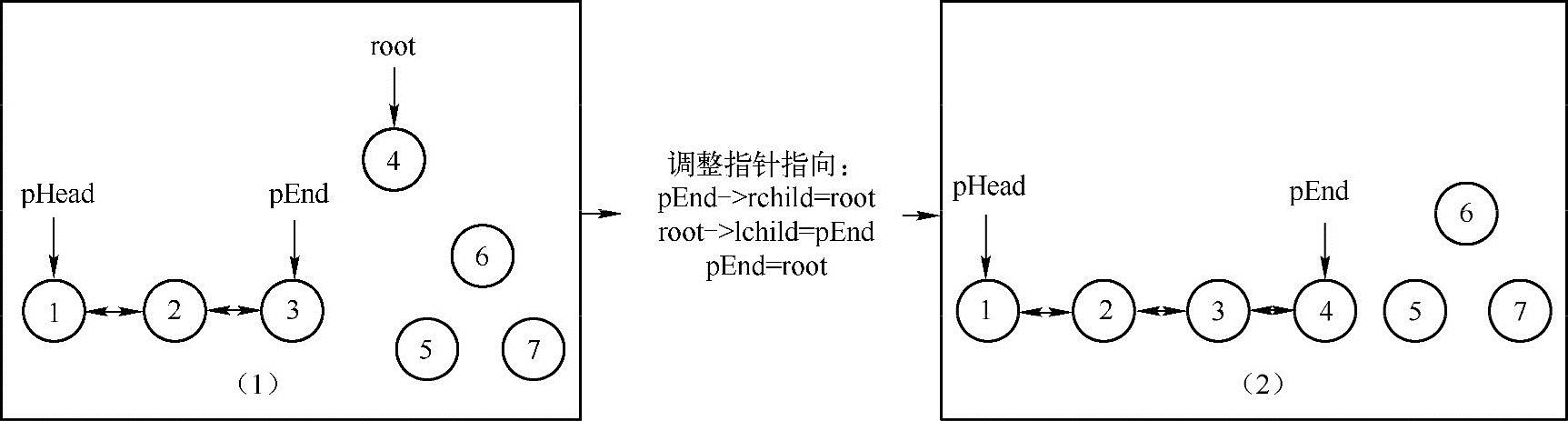
实现代码如下：

程序的运行结果如下：

转换后双向链表正向遍历：1 2 3 4 5 6 7

转换后双向链表逆向遍历：7 6 5 4 3 2 1

算法性能分析：

这种方法与二叉树的中序遍历有着相同的时间复杂度O（N）。此外，这种方法只用了两个额外的变量pHead与pEnd来记录双向链表的首尾结点，因此，空间复杂度为O（1）。

3.7 如何判断一个数组是否是二元查找树后序遍历的序列

【出自ALBB面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

输入一个整数数组，判断该数组是否是某二元查找树的后序遍历的结果。如果是，那么返回true，否则返回false。例如数组{1，3，2，5，7，6，4}就是下图中二叉树的后序遍历序列。

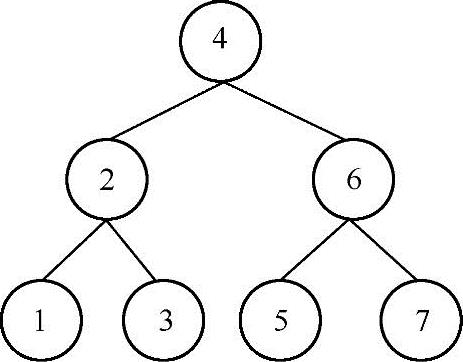
分析与解答：

二元查找树的特点是：对于任意一个结点，它的左子树上所有结点的值都小于这个结点的值，它的右子树上所有结点的值都大于这个结点的值。根据它的这个特点以及二元查找树后序遍历的特点，可以看出，这个序列的最后一个元素一定是树的根结点（上图中的结点4），然后在数组中找到第一个大于根结点4的值5，那么结点5之前的序列（1，3，2）对应的结点一定位于结点4的左子树上，结点5（包含这个结点）后面的序列一定位于结点4的右子树上（也就是说结点5后面的所有值都应该大于或等于4）。对于结点4的左子树遍历的序列{1，3，2}以及右子树的遍历序列{5，7，6}可以采用同样的方法来分析，因此，可以通过递归方法来实现，实现代码如下：

程序的运行结果如下：

1 3 2 5 7 6 4是某一二元查找树的后序遍历序列

算法性能分析：

这种方法对数组只进行了一次遍历，因此，时间复杂度为O（N）。

3.8 如何找出排序二叉树上任意两个结点的最近共同父结点

【出自WR面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

对于一棵给定的排序二叉树，求两个结点的共同父结点，例如在下图中，结点1和结点5的共同父结点为3。

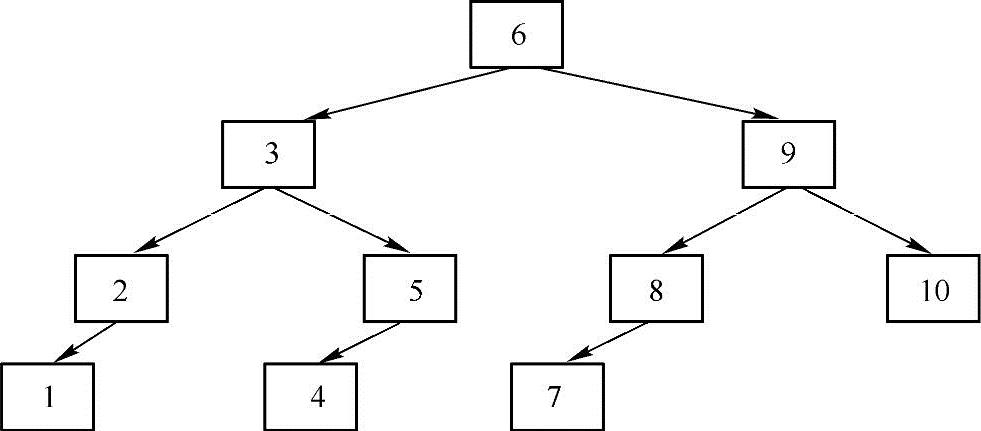
分析与解答：

方法一：路径对比法

对于一棵二叉树的两个结点，如果知道了从根结点到这两个结点的路径，就可以很容易地找出它们最近的公共父结点。因此，可以首先分别找出从根结点到这两个结点的路径（例如上图中从根结点到结点1的路径为6-＞3-＞2-＞1，从根结点到结点5的路径为6-＞3-＞5）；然后遍历这两条路径，只要是相等的结点都是它们的父结点，找到最后一个相等的结点即为离它们最近的共同父结点，在这个例子中，结点3就是它们共同的父结点。为了便于理解，这里仍然使用3.2节中构造的二叉树的方法。示例代码如下：

程序的运行结果如下：

1与5的最近公共父结点为3

算法性能分析：

当获取二叉树从根结点root到node结点的路径时，最坏的情况就是把树中所有结点都遍历了一遍，这个操作的时间复杂度为O（N），再分别找出从根结点到两个结点的路径，找它们最近的公共父结点的时间复杂度也为O（N），因此，这种方法的时间复杂度为O（N）。此外，这种方法用栈保存了从根结点到特定结点的路径，在最坏的情况下，这个路径包含了树中所有的结点，因此，空间复杂度也为O（N）。

很显然，这种方法还不够理想。下面介绍另外一种能降低空间复杂度的方法。

方法二：结点编号法

根据3.1节中介绍的性质5，可以把二叉树看成是一棵完全二叉树（不管实际的二叉树是否为完全二叉树，二叉树中的结点都可以按照完全二叉树中对结点编号的方式进行编号），下图为对二叉树中的结点按照完全二叉树中结点的编号方式进行编号后的结果，结点右边的数字为其对应的编号。

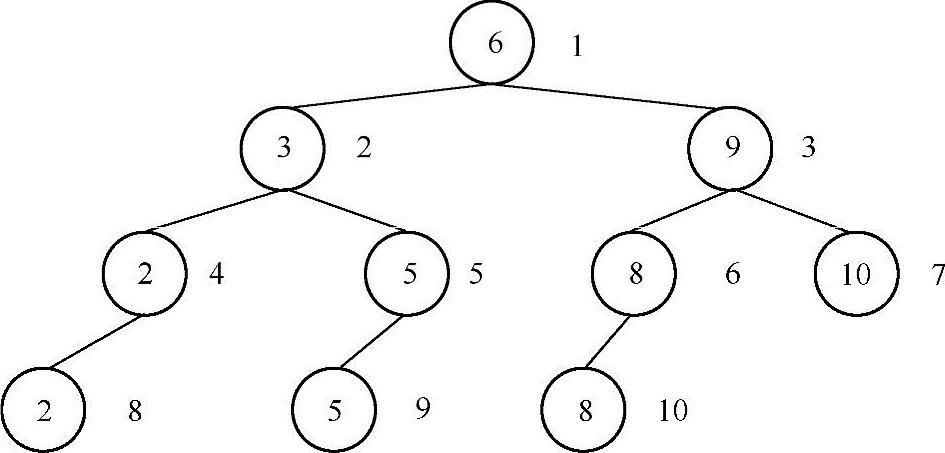
根据3.1节性质5可以知道，一个编号为n的结点，它的父亲结点的编号为n/2。假如要求node1与node2的最近的共同父结点，首先把这棵树看成是一棵完全二叉树（不管结点是否存在），分别求得这两个结点的编号n1，n2。然后每次找出n1与n2中较大的值除以2，直到n1==n2为止，此时n1或n2的值对应结点的编号就是它们最近的共同父结点的编号，接着可以根据这个编号信息找到对应的结点，具体方法是通过观察二叉树中结点的编号可以发现：首先把根结点root看成1，求root的左孩子编号的方法为把root对应的编号看成二进制，然后向左移一位，末尾补0，如果是root的右孩子，则末尾补1，因此，通过结点位置的二进制码就可以确定这个结点。例如结点3的编号为2（二进制10），它的左孩子的求解方法为10，向左移一位末尾补0，可以得到二进制100（十进制4），位置为4的结点的值为2。从这个特性可以得出通过结点位置信息获取结点的方法，例如要求位置4的结点，4的二进制码为100，由于1代表根结点，接下来的一个0代表是左子树root.lchild，最后一个0也表示左子树root.lchild.lchild，通过这种方法非常容易根据结点的编号找到对应的结点。实现代码如下：

算法性能分析：

这种方法的时间复杂度也为O（N），与方法一相比，在求解的过程中只用了个别的几个变量，因此，空间复杂度为O（1）。

方法三：后序遍历法

很多与二叉树相关的问题都可以通过对二叉树的遍历方法进行改装而求解。对于本题而言，可以通过对二叉树的后序遍历进行改编而得到。具体思路是：查找结点node1与结点node2的最近共同父结点可以转换为找到一个结点node，使得node1与node2分别位于结点node的左子树或右子树中。例如题目中的图，结点1与结点5的最近共同父结点为结点3，因为结点1位于结点3的左子树上，而结点5位于结点3的右子树上。实现代码如下：

把方法一中的FindParentNode替换为本方法的FindParentNode，可以得到同样的输出结果。

算法性能分析：

这种方法与二叉树的后序遍历方法有着相同的时间复杂度O（N）。

引申：如何计算二叉树中两个结点的距离

【出自TX面试题】

题目描述：

在没有给出父结点的条件下，计算二叉树中两个结点的距离。两个结点之间的距离是从一个结点到达另一个结点所需的最小的边数。例如，给出下面的二叉树：

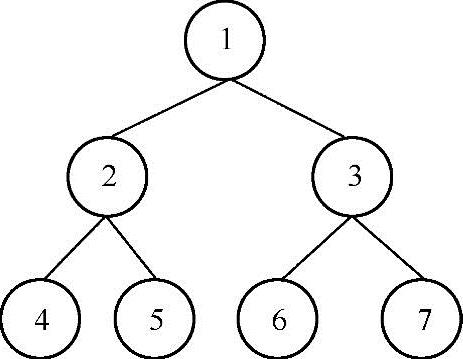
Dist（4，5）=2，Dist（4，6）=4。

分析与解答：

对于给定的二叉树root，只要能找到两个结点n1与n2最低的公共父结点parent，那么就可以通过下面的公式计算出这两个结点的距离：

Dist（n1，n2）=Dist（root，n1）+Dist（root，n2）-2*Dist（root，parent）

3.9 如何复制二叉树

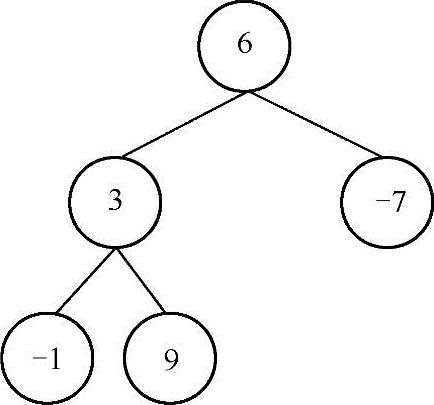
【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个二叉树根结点，复制该树，返回新建树的根结点。

分析与解答：

用给定的二叉树的根结点root来构造新的二叉树的方法：首先创建新的结点dupTree，然后根据root结点来构造dupTree结点（dupTree.data=root.data），最后分别用root的左右子树来构造dupTree的左右子树。根据这个思路可以实现二叉树的复制，使用递归方式实现的代码如下：

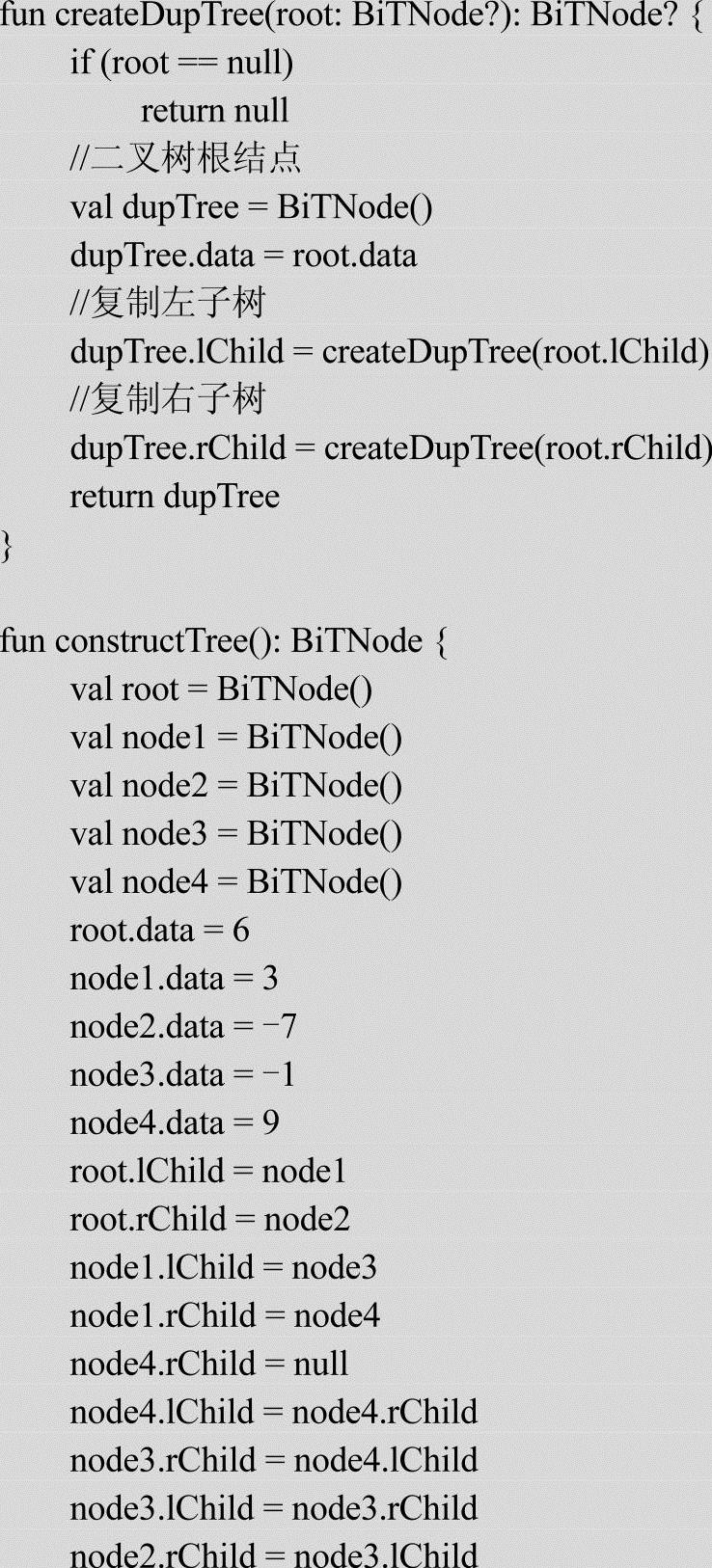
程序的运行结果如下：

原始二叉树中序遍历：-1 3 9 6 -7

新的二叉树中序遍历：-1 3 9 6 -7

算法性能分析：

这种方法对给定的二叉树进行了一次遍历，因此，时间复杂度为O（N），此外，这种方法需要申请N个额外的存储空间来存储新的二叉树。

3.10 如何在二叉树中找出与输入整数相等的所有路径

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

从树的根结点开始往下访问一直到叶子结点经过的所有结点形成一条路径。找出所有的这些路径，使其满足这条路径上所有结点数据的和等于给定的整数。例如：给定如下二叉树与整数8，满足条件的路径为6-＞3-＞-1（6+3-1=8）。

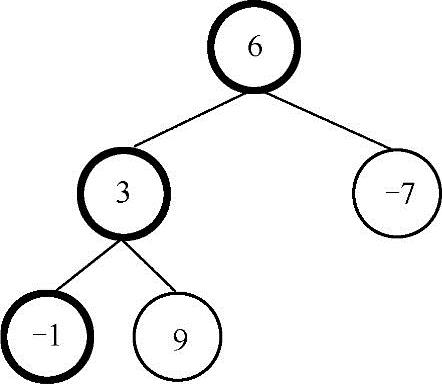
分析与解答：

可以通过对二叉树的遍历找出所有的路径，然后判断各条路径上所有结点的值的和是否与给定的整数相等，如果相等，则打印出这条路径。具体实现方法可以通过对二叉树进行先序遍历来实现，实现思路为对二叉树进行先序遍历，把遍历的路径记录下来，当遍历到叶子结点时，判断当前的路径上所有结点数据的和是否等于给定的整数，如果相等则输出路径信息，示例代码如下：

程序的运行结果如下：

满足路径结点和等于8的路径为：63-1

算法性能分析：

这种方法与二叉树的先序遍历有着相同的时间复杂度O（N），此外，这种方法用一个数组存放遍历路径上结点的值，在最坏的情况下时间复杂度为O（N）（所有结点只有左子树，或所有结点只有右子树），因此，空间复杂度为O（N）。

3.11 如何对二叉树进行镜像反转

【出自TB笔试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

二叉树的镜像就是二叉树对称的二叉树，就是交换每一个非叶子结点的左子树指针和右子树指针，如下图所示，请写出能实现该功能的代码。注意：请勿对该树做任何假设，它不一定是平衡树，也不一定有序。

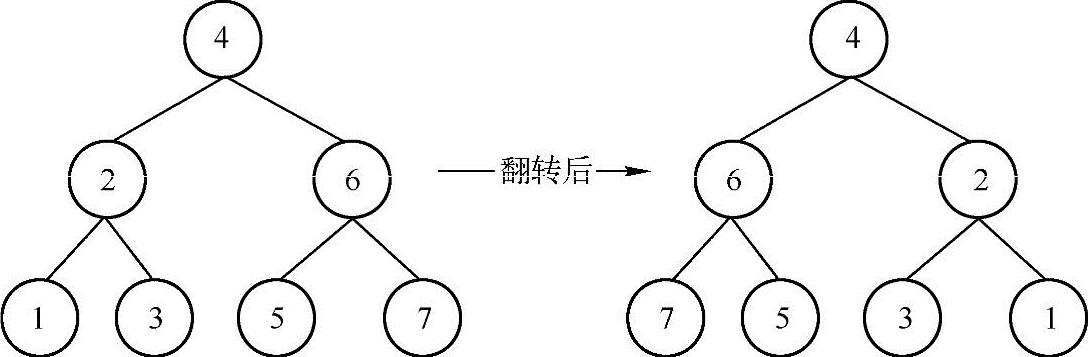
分析与解答：

从上图可以看出，要实现二叉树的镜像反转，只需交换二叉树中所有结点的左右孩子即可。由于对所有的结点都做了同样的操作，因此，可以用递归的方法来实现，由于需要调用printTreeLayer层序打印二叉树，这种方法中使用了队列来实现，实现代码如下：

程序的运行结果如下：

二叉树层序遍历结果为：4 2 6 1 3 5 7

反转后的二叉树层序遍历结果为：4 6 2 7 5 3 1

算法性能分析：

由于对给定的二叉树进行了一次遍历，因此，时间复杂度为O（N）。

3.12 如何在二叉排序树中找出第一个大于中间值的结点

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

对于一棵二叉排序树，令f=（最大值+最小值）/2，设计一个算法，找出距离f值最近、大于f值的结点。例如，下图所给定的二叉排序树中，最大值为7，最小值为1，因此，f=（1+7）/2=4，那么在这棵二叉树中，距离结点4最近并且大于4的结点为5。

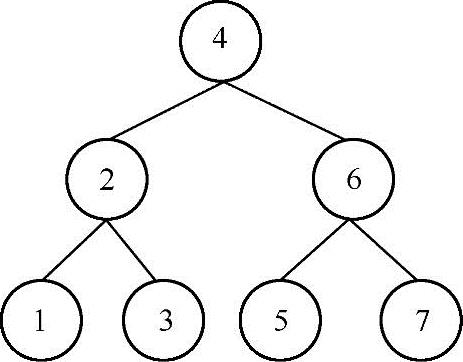
分析与解答：

首先需要找出二叉排序树中的最大值与最小值。由于二叉排序树的特点是：对于任意一个结点，它的左子树上所有结点的值都小于这个结点的值，它的右子树上所有结点的值都大于这个结点的值。因此，在二叉排序树中，最小值一定是最左下的结点，最大值一定是最右下的结点。根据最大值与最小值很容易就可以求出f的值。接下来对二叉树进行中序遍历。如果当前结点的值小于f，那么在这个结点的右子树中接着遍历，否则遍历这个结点的左子树。实现代码如下：

程序的运行结果如下：

5

算法性能分析：

这种方法在查找最大结点与最小结点时的时间复杂度为O（h），h为二叉树的高度，对于有N个结点的二叉排序树，最大的高度为O（N），最小的高度为O（log₂^N）。同理，在查找满足条件的结点的时候，时间复杂度也是O（h）。综上所述，这种方法的时间复杂度在最好的情况下是O（log₂^N），最坏的情况下为O（N）。

3.13 如何在二叉树中找出路径最大的和

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一棵二叉树，求各个路径的最大和，路径可以以任意结点作为起点和终点。比如给定以下二叉树：

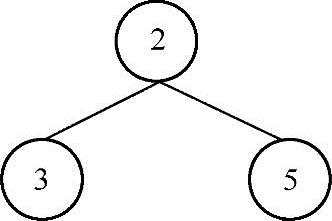
返回10。

分析与解答：

本题可以通过对二叉树进行后序遍历来解决，具体思路如下：

对于当前遍历到的结点root，假设已经求出在遍历root结点前最大的路径和为max。

（1）求出以root.left为起始结点，叶子结点为终结点的最大路径和为maxLeft。

（2）同理求出以root.right为起始结点，叶子结点为终结点的最大路径和maxRight。

包含root结点的最长路径可能包含如下三种情况：

（1）leftMax=root.val+maxLeft（左子树最大路径和可能为负）。

（2）rightMax=root.val+maxRight（右子树最大路径和可能为负）。

（3）allMax=root.val+maxLeft+maxRight（左右子树的最大路径和都不为负）。

因此，包含root结点的最大路径和为tmpMax=max（leftMax，rightMax，allMax）。

在求出包含root结点的最大路径后，如果tmpMax＞max，那么更新最大路径和为tmpMax。

实现代码如下：

程序的运行结果如下：

10

算法性能分析：

二叉树后序遍历的时间复杂度为O（N），因此，这种方法的时间复杂度也为O（N）。

3.14 如何实现反向DNS查找缓存

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

反向DNS查找指的是使用Internet IP地址查找域名。例如，如果在浏览器中输入74.125.200.106，它会自动重定向到google.in。

如何实现反向DNS查找缓存？

分析与解答：

要想实现反向DNS查找缓存，主要需要完成如下功能：

（1）将IP地址添加到缓存中的URL映射。

（2）根据给定IP地址查找对应的URL。

对于本题，常见的一种解决方案是使用哈希法（使用hashmap来存储IP地址与URL之间的映射关系），由于这种方法相对比较简单，这里不再赘述。下面重点介绍另外一种方法：Trie树。这种方法的主要优点如下：

（1）使用Trie树，在最坏的情况下的时间复杂度为O（1），而哈希方法在平均情况下的时间复杂度为O（1）。

（2）Trie树可以实现前缀搜索（对于有相同前缀的IP地址，可以寻找所有的URL）。

当然，由于树这种数据结构本身的特性，所以使用树结构的一个最大的缺点就是需要耗费更多的内存，但是对于本题而言，这却不是一个问题，因为InternetIP地址只包含有11个字母（0到9和.）。所以，本题实现的主要思路是：在Trie树中存储IP地址，而在最后一个结点中存储对应的域名。实现代码如下：

程序的运行结果如下：

找到了IP对应的URL：

121.57.61.129--＞www.samsung.net

显然，由于上述算法中涉及的IP地址只包含特定的11个字符（数字和.），所以，该算法也有一些异常情况未处理，例如不能处理用户输入的不合理的IP地址，有兴趣的读者可以继续朝着这个思路完善后面的算法。

第4章 数组

数组是某种类型的数据按照一定的顺序组成的数据的集合。如果将有限个类型相同的变量的集合命名，那么这个称为数组名。组成数组的各个变量称为数组的分量，也称为数组的元素，有时也称为下标变量。用于区分数组的各个元素的数字编号称为下标。

数组是最基本的数据结构，关于数组的面试笔试题在企业的招聘中也是屡见不鲜，求解此类题目，不仅需要扎实的编程基础，更需要清晰的思路与方法。本章列出的众多数组相关面试笔试题，都非常具有代表性，需要读者重点关注。

4.1 如何找出数组中唯一的重复元素

【出自BD面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

数字1～1000放在含有1001个元素的数组中，其中只有唯一的一个元素值重复，其他数字均只出现一次。设计一个算法，将重复元素找出来，要求每个数组元素只能访问一次。如果不使用辅助存储空间，能否设计一个算法实现？

分析与解答：

方法一：空间换时间法

拿到题目，首先需要做的就是分析题目所要达到的目标以及其中的限定条件。从题目的描述中可以发现，本题的目标就是在一个有且仅有一个元素值重复的数组中找出这个唯一的重复元素，而限定条件就是每个数组元素只能访问一次，并且不许使用辅助存储空间。很显然，从前面对Hash法的分析中可知，如果题目没有对是否可以使用辅助数组做限制的话，最简单的方法就是使用Hash法。

当使用Hash法时，具体过程如下所示：首先定义一个长度为1000的Hash数组，将Hash数组中的元素值都初始化为0，将原数组中的元素逐一映射到该Hash数组中，当对应的Hash数组中的值为0时，置该Hash数组中该处的值为1，当对应的Hash数组中该处的值为1时，表明该位置的数在原数组中是重复的，输出即可。

示例代码如下：

程序的运行结果如下：

3

算法性能分析：

上述方法是一种典型的以空间换时间的方法，它的时间复杂度为O（N），空间复杂度为O（N），很显然，在题目没有明确限制的情况下，上述方法不失为一种好方法，但是，由于题目要求不能用额外的辅助空间，所以，上述方法不可取，是否存在其他满足题意的方法呢？

方法二：累加求和法

计算机技术与数学本身是一家，抛开计算机专业知识不提，上述问题其实可以回归成一个数学问题。数学问题的目标是在一个数字序列中寻找重复的那个数。根据题目意思可以看出，1～1000个数中除了唯一一个数重复以外，其他各数有且仅有出现一次，由数学性质可知，这1001个数包括1～1000中的每一个数各1次，外加1～1000中某一个数，很显然，1001个数中有1000个数是固定的，唯一一个不固定的数也知道其范围（1～1000中某一个数），那么最容易想到的方法就是累加求和法。

所谓累加求和法，指的是将数组中的所有N+1（此处N的值取1000）个元素相加，然后用得到的和减去1+2+3+…N（此处N的值为1000）的和，得到的差即为重复的元素的值。这一点不难证明。

由于1001个数的数据量较大，不方便说明以上算法。为了简化问题，以数组序列{1，3，4，2，5，3}为例。该数组长度为6，除了数字3以外，其他4个数字没有重复。按照上述方法，首先，计算数组中所有元素的和sumb，sumb=1+3+4+2+5+3=18，数组中只包含1～5的数，计算1～5一共5个数字的和suma，suma=1+2+3+4+5=15；所以，重复的数字的值为sumb^- suma=3。由于本方法的代码实现较为简单，此处就不提供代码了，有兴趣的读者可以自己实现。

算法性能分析：

上述方法的时间复杂度为O（N），空间复杂度为O（1）。

在使用求和法计算时，需要注意一个问题，即当数据量巨大时，有可能会导致计算结果溢出。以本题为例，1～1000范围内的1000个数累加，其和为（1+1000）×1000/2，即500500，普通的int型变量能够表示出来，所以，本题中不存在此问题。但如果累加的数值巨大，就很有可能溢出了。

此处是否还可以继续发散一下，如果累加求和法能够成立的话，累乘求积法是不是也可以成立呢？只是累加求积法在使用的过程中很有可能会存在数据越界的情况，如果再由此定义一个大数乘法，那就有点得不偿失了。所以，求积的方式理论上是成立的，只是在实际的使用过程中可操作性不强而已，一般更加推荐累加求和法。

方法三：异或法

采用以上累加求和的方法，虽然能够解决本题的问题，但也存在一个潜在的风险，就是当数组中的元素值太大或者数组太长时，计算的和值有可能会出现溢出的情况，进而无法求解出数组中的唯一重复元素。

鉴于求和法存在的局限性，可以采用位运算中异或的方法。根据异或运算的性质可知，当相同元素异或时，其运算结果为0，当相异元素异或时，其运算结果为非0，任何数与数字0进行异或运算，其运算结果为该数。本题中，正好可以使用到此方法，即将数组里的元素逐一进行异或运算，得到的值再与数字1、2、3…N进行异或运算，得到的最终结果即为所求的重复元素。

以数组{1，3，4，2，5，3}为例。（1^3^4^2^5^3）^（1^2^3^4^5）=（1^1）^（2^2）^（3^3^3）^（4^4）^（5^5）=0^0^3^0^0=3。

示例代码如下：

程序员的运行结果如下：

3

算法性能分析：

上述方法的时间复杂度为O（N），也没有申请辅助的存储空间。

方法四：数据映射法

数组取值操作可以看作一个特殊的函数f：D→R，定义域为下标值0～1000，值域为1～1000。如果对任意一个数i，把f（i）叫作它的后继，i叫f（i）的前驱。0只有后继，没有前驱，其他数字既有后继也有前驱，重复的那个数字有两个前驱，将利用这些特征。

采用此种方法，可以发现一个规律，即从0开始画一个箭头指向它的后继，从它的后继继续指向后继的后继，这样，必然会有一个结点指向之前已经出现过的数，即为重复的数。

利用下标与单元中所存储的内容之间的特殊关系，进行遍历访问单元，一旦访问过的单元赋予一个标记（把数组中元素变为它的相反数），利用标记作为发现重复数字的关键。

以数组array={1，3，4，3，5，2}为例。从下标0开始遍历数组：

（1）array[0]的值为1，说明没有被遍历过，接下来遍历下标为1的元素，同时标记已遍历过的元素（变为相反数）：array={-1，3，4，3，5，2}。

（2）array[1]的值为3，说明没被遍历过，接下来遍历下标为3的元素，同时标记已遍历过的元素：array={-1，-3，4，3，5，2}。

（3）array[3]的值为3，说明没被遍历过，接下来遍历下标为3的元素，同时标记已遍历过的元素：array={-1，-3，4，-3，5，2}。

（4）array[3]的值为-3，说明3已经被遍历过了，找到了重复的元素。

示例代码如下：

算法说明：

因为每个数在数组中都有自己应该在的位置，如果一个数是在自己应该在的位置（在本题中就是它的值就是它的下标，即所在的位置），那永远不会对它进行调换，也就是不会访问到它，除非它就是那个多出的数，那与它相同的数访问到它的时候就是结果了；如果一个数的位置是鸠占鹊巢，所在的位置不是它应该待的地方，那它会去找它应该在的位置，在它位置的数也会去找它应该在的位置，碰到了负数，也就是说已经出现了这个数，所以，就也得出了结果。

算法性能分析：

上述方法的时间复杂度为O（N），也没有申请辅助的存储空间。

这种方法的缺点是修改了数组中元素的值，当然也可以在找到重复元素之后对数组进行一次遍历，把数组中的元素改为它的绝对值的方法来恢复对数组的修改。

方法五：环形相遇法

该方法就是采用类似于单链表是否存在环的方法进行问题求解。“判断单链表是否存在环”是一个非常经典的问题，同时单链表可以采用数组实现，此时每个元素值作为next指针指向下一个元素。本题可以转化为“已知一个单链表中存在环，找出环的入口点”这种想法。具体思路如下：将array[i]看作第i个元素的索引，即：array[i]-＞array[array[i]]-＞array[array[array[i]]]-＞array[array[array[array[i]]]]-＞…最终形成一个单链表，由于数组a中存在重复元素，则一定存在一个环，且环的入口元素即为重复元素。

该题的关键在于，数组array的大小是n，而元素的范围是[1，n-1]，所以，array[0]不会指向自己，进而不会陷入错误的自循环。如果元素的范围中包含0，则该题不可直接采用该方法。以数组序列{1，3，4，2，5，3}为例。按照上述规则，这个数组序列对应的单链表如下图所示：

从上图可以看出这个链表有环，且环的入口点为3，所以，这个数组中重复元素为3。

在实现的时候可以参考求单链表环的入口点的算法：用两个速度不同的变量slow和fast来访问，其中，slow每次前进一步，fast每次前进两步。在有环结构中，它们总会相遇。接着从数组首元素与相遇点开始分别遍历，每次各走一步，它们必定相遇，且相遇第一点为环入口点。

示例代码如下：

程序的运行结果如下：

3

算法性能分析：

上述方法的时间复杂度为O（N），也没有申请辅助的存储空间。

当数组中的元素不合理的时候，上述算法有可能会有数组越界的可能性，因此，为了安全性和健壮性，可以在执行fast=array[array[fast]]；slow=array[slow]；操作的时候分别检查array[slow]与array[fast]的值是否会越界，如果越界，则说明提供的数据不合法。

引申：对于一个给定的自然数N，有一个N+M个元素的数组，其中存放了小于等于N的所有自然数，求重复出现的自然数序列{X}

分析与解答：

对于这个扩展需要，已经标记过的数字在后面一定不会再访问到，除非它是重复的数字，也就是说只要每次将重复数字中的一个改为靠近N+M的自然数，让遍历能访问到数组后面的元素，就能将整个数组遍历完。此种方法非常不错，而且它具有可扩展性。

程序的运行结果如下：

3 5

算法性能分析：

上述方法的时间复杂度为O（N），也没有申请辅助的存储空间。

当数组中的元素不合理的时候，上述方法有可能会有数组越界的可能性，也有可能会进入死循环，为了避免这种情况发生，可以增加适当的安全检查代码。

4.2 如何查找数组中元素的最大值和最小值

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定数组a1，a2，a3，…an，要求找出数组中的最大值和最小值。假设数组中的值两两各不相同。

分析与解答：

虽然题目没有时间复杂度与空间复杂度的要求，但是给出的算法的时间复杂度肯定是越低越好。

方法一：蛮力法

查找数组中元素的最大值与最小值并非是一件困难的事情，最容易想到的方法就是蛮力法。具体过程如下：首先定义两个变量max与min，分别记录数组中最大值与最小值，并将其都初始化为数组的首元素的值，然后从数组的第二个元素开始遍历数组元素，如果遇到的数组元素的值比max大，则该数组元素的值为当前的最大值，并将该值赋给max，如果遇到的数组元素的值比min小，则该数组元素的值为当前的最小值，并将该值赋给min。

算法性能分析：

上述方法的时间复杂度为O（n），但很显然，以上这种方法称不上是最优算法，因为最差情况下比较的次数达到了2n-2次（数组第一个元素首先赋值给max与min，接下来的n-1个元素都需要分别跟max与min比较一次，一次比较次数为2n-2），最好的情况下比较次数为n-1。是否可以将比较次数降低呢？回答是肯定的，分治法就是一种高效的方法。

方法二：分治法

分治法就是将一个规模为n的、难以直接解决的大问题，分割为k个规模较小的子问题，采取各个击破、分而治之的策略得到各个子问题的解，然后将各个子问题的解进行合并，从而得到原问题的解的一种方法。

本题中，当采用分治法求解时，就是将数组两两一对分组，如果数组元素个数为奇数个，就把最后一个元素单独分为一组，然后分别对每一组中相邻的两个元数进行比较，把两者中值小的数放在数组的左边，值大的数放在数组右边，只需要比较n/2次就可以将数组分组完成。然后可以得出结论：最小值一定在每一组的左边部分，最大值一定在每一组的右边部分，接着只需要在每一组的左边部分找最小值，右边部分找最大值，查找分别需要比较n/2-1次和n/2-1次。因此，总共比较的次数大约为n/2×3=3n/2-2次。

实现代码如下：

程序的运行结果如下：

max=40

min=1

方法三：变形的分治法

除了以上所示的分治法以外，还有一种分治法的变形，其具体步骤如下：将数组分成左右两部分，先求出左半部分的最大值和最小值，再求出右半部分的最大值和最小值，然后综合起来，左右两部分的最大值中的较大值即为合并后的数组的最大值，左右两部分的最小值中的较小值即为合并后的数组的最小值，通过此种方法即可求合并后的数组的最大值与最小值。

以上过程是个递归过程，对于划分后的左右两部分，同样重复这个过程，直到划分区间内只剩一个元素或者两个元素为止。

示例代码如下：

算法性能分析：

这种方法与方法二的思路从本质上讲是相同的，只不过这种方法是使用递归的方式实现的，因此，比较次数为3n/2-2。

4.3 如何找出旋转数组中的最小元素

【出自YMX面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

把一个有序数组最开始的若干个元素搬到数组的末尾，称之为数组的旋转。输入一个排好序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3，4，5，1，2}为数组{1，2，3，4，5}的一个旋转，该数组的最小值为1。

分析与解答：

其实这是一个非常基本和常用的数组操作，它的描述如下：

有一个数组X[0…n-1]，现在把它分为两个子数组：x1[0…m]和x2[m+1…n-1]，交换这两个子数组，使数组x由x1x2变成x2x1，例如x={1，2，3，4，5，6，7，8，9}，x1={1，2，3，4，5}，x2={6，7，8，9}，交换后，x={6，7，8，9，1，2，3，4，5}。

对于本题的解决方案，最容易想到的，也是最简单的方法就是直接遍历法。但是这种方法显然没有用到题目中旋转数组的特性，因此，它的效率比较低下。下面介绍一种比较高效的二分查找法。

通过数组的特性可以发现，数组元素首先是递增的，然后突然下降到最小值，然后再递增。虽然如此，但是还有下面三种特殊情况需要注意：

（1）数组本身是没有发生过旋转的，是一个有序的数组，例如序列{1，2，3，4，5，6}。

（2）数组中元素值全部相等，例如序列{1，1，1，1，1，1}。

（3）数组中元素值大部分都相等，例如序列{1，0，1，1，1，1}。

通过旋转数组的定义可知，经过旋转之后的数组实际上可以划分为两个有序的子数组，前面的子数组的元素值都大于或者等于后面子数组的元素值。可以根据数组元素的这个特点，采用二分查找的思想不断缩小查找范围，最终找出问题的解决方案，具体实现思路如下所示：

按照二分查找的思想，给定数组arr，首先定义两个变量low和high，分别表示数组的第一个元素和最后一个元素的下标。按照题目中对旋转规则的定义，第一个元素应该是大于或者等于最后一个元素的（当旋转个数为0，即没有旋转的时候，要单独处理，直接返回数组第一个元素）。接着遍历数组中间的元素arr[mid]，其中mid=（high+low）/2。

（1）如果arr[mid]＜arr[mid-1]，则arr[mid]一定是最小值。

（2）如果arr[mid+1]＜arr[mid]，则arr[mid+1]一定是最小值。

（3）如果arr[high]＞arr[mid]，则最小值一定在数组左半部分。

（4）如果arr[mid]＞arr[low]，则最小值一定在数组右半部分。

（5）如果arr[low]==arr[mid]且arr[high]==arr[mid]，则此时无法区分最小值是在数组的左半部分还是右半部分（例如：{2，2，2，2，1，2}，{2，1，2，2，2，2，2}）。在这种情况下，只能分别在数组的左右两部分找最小值minL与minR，最后求出minL与minR的最小值。

示例代码如下：

程序的运行结果如下：

1

0

算法性能分析：

一般而言，二分查找的时间复杂度为O（log₂^N），对于这道题而言，大部分情况下时间复杂度为O（log₂^N），只有每次都满足上述条件（5）的时候才需要对数组中所有元素都进行遍历，因此，这种方法在最坏的情况下的时间复杂度为O（N）。

引申：如何实现旋转数组功能

分析与解答：

先分别把两个子数组的内容交换，然后把整个数组的内容交换，即可得到问题的解。

以数组x1{1，2，3，4，5}与数组x2{6，7，8，9}为例，交换两个数组后，x1={5，4，3，2，1}，x2={9，8，7，6}，即x={5，4，3，2，1，9，8，7，6}。交换整个数组后，x={6，7，8，9，1，2，3，4，5}

示例代码如下：

程序的运行结果如下：

4 5 1 2 3

算法性能分析：

由于这种方法需要遍历两次数组，因此，它的时间复杂度为O（N）。而交换两个变量的值，只需要使用一个辅助储存空间，所以，它的空间复杂度为O（1）。

4.4 如何找出数组中丢失的数

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个由n-1个整数组成的未排序的数组序列，其元素都是1到n中的不同的整数。请写出一个寻找数组序列中缺失整数的线性时间算法。

分析与解答：

方法一：累加求和

首先分析一下数学性质。假设缺失的数字是X，那么这n-1个数一定是1～n之间除了X以外的所有数，试想一下，1～n一共n个数的和是可以求出来的，数组中的元素的和也是可以求出来的，二者相减，其值是不是就是缺失的数字X的值呢？

为了更好地说明上述方法，举一个简单的例子。假设数组序列为{2，1，4，5}一共4个元素，n的值为5，要想找出这个缺失的数字，可以首先对1～5这五个数字求和，求和结果为15（1+2+3+4+5=15），而数组元素的和为array[0]+array[1]+array[2]+array[3]=2+1+4+5=12，所以，缺失的数字为15-12=3。

通过上面的例子可以很容易形成以下具体思路：定义两个数suma与sumb，其中，suma表示的是这n-1个数的和，sumb表示的是这n个数的和，很显然，缺失的数字的值即为sumb-suma的值。

示例代码如下：

程序的运行结果如下：

6

算法性能分析：

这种方法的时间复杂度为O（N）。需要注意的是，在求和的过程中，计算结果有溢出的可能性。所以，为了避免这种情况的发生，在进行数学运算时，可以考虑位运算，毕竟位运算性能最好，下面介绍如何用位运算来解决这个问题。

方法二：异或法

在解决这个问题前，首先回顾一下异或运算的性质。简单点说，在进行异或运算时，当参与运算的两个数相同时，异或结果为假，当参与异或运算的两个数不相同时，异或结果为真。

1～n这n个数异或的结果为a=1^2^3^…^n。假设数组中缺失的数为m，那么数组中这n-1个数异或的结果为b=1^2^3^…（m-1）^（m+1）^…^n。由此可知，a^b=（1^1）^（2^2）^…（m-1）^（m-1）^m^（m+1）^（m+1）^…^（n^n）=m。根据这个公式可以得知本题的主要思路是：定义两个数a与b，其中，a表示的是1～n这n个数的异或运算结果，b表示的是数组中的n-1个数的异或运算结果，缺失的数字的值即为a^b的值。

实现代码如下：

算法性能分析：

这种方法在计算结果a的时候对数组进行了一次遍历，时间复杂度为O（N），接着在计算b的时候循环执行的次数为N，时间复杂度也为O（N）。因此，这种方法的时间复杂度为O（N）。

4.5 如何找出数组中出现奇数次的数

【出自BD面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

数组中有N+2个数，其中，N个数出现了偶数次，两个数出现了奇数次（这两个数不相等），请用O（1）的空间复杂度，找出这两个数。注意：不需要知道具体位置，只需要找出这两个数。

分析与解答：

方法一：Hash法

对于本题而言，定义一个HashMap表，把数组元素的值作为key，遍历整个数组，如果key值不存在，则将value设为1，如果key值已经存在，则翻转该值（如果为0，则翻转为1；如果为1，则翻转为0），在完成数组遍历后，Hash表中value为1的就是出现奇数次的数。

例如：给定数组={3，5，6，6，5，7，2，2}；

首先遍历3，HashMap中的元素为：＜3，1＞；

遍历5，HashMap中的元素为：＜3，1＞，＜5，1＞；

遍历6，HashMap中的元素为：＜3，1＞，＜5，1＞，＜6，1＞；

遍历6，HashMap中的元素为：＜3，1＞，＜5，1＞，＜6，0＞；

遍历5，HashMap中的元素为：＜3，1＞，＜5，0＞，＜6，0＞；

遍历7，HashMap中的元素为：＜3，1＞，＜5，0＞，＜6，0＞，＜7，1＞；

遍历2，HashMap中的元素为：＜3，1＞，＜5，0＞，＜6，0＞，＜7，1＞，＜2，1＞；

遍历2，HashMap中的元素为：＜3，1＞，＜5，0＞，＜6，0＞，＜7，1＞，＜2，0＞；

显然，出现1次的数组元素为3和7。

实现代码如下：

程序输出如下：

3

7

性能分析：

这种方法对数组进行了一次遍历，时间复杂度为O（n）。但是申请了额外的存储过程来记录数据出现的情况，因此，空间复杂度为O（n）。

方法二：异或法

根据异或运算的性质不难发现，任何一个数字异或它自己其结果都等于0。所以，对于本题中的数组元素而言，如果从头到尾依次异或每一个元素，那么异或运算的结果自然也就是那个只出现奇数次的数字，因为出现偶数次的数字会通过异或运算全部消掉。

但是通过异或运算，也仅仅只是消除了所有出现偶数次数的数字，最后异或运算的结果肯定是那两个出现了奇数次的数异或运算的结果。假设这两个出现奇数次的数分别为a与b，根据异或运算的性质，将二者异或运算的结果记为c，由于a与b不相等，所以，c的值自然也不会为0，此时只需知道c对应的二进制数中某一个位为1的位数N，例如，十进制数44可以由二进制数00101100表示，此时可取N=2或者3，或者5，然后将c与数组中第N位为1的数进行异或，异或结果就是a和b中的一个，然后用c异或其中一个数，就可以求出另外一个数了。

通过上述方法为什么就能得到问题的解呢？其实很简单，因为c中第N位为1表示a或b中有一个数的第N位也为1，假设该数为a，那么，当将c与数组中第N位为1的数进行异或时，也就是将x与a外加上其他第N位为1的出现过偶数次的数进行异或，化简即为x与a异或，结果即为b。

示例代码如下：

程序的运行结果如下：

3 7

算法性能分析：

这种方法首先对数组进行了一次遍历，其时间复杂度为O（N），接着找result对应二进制数中位值为1的位数，时间复杂度为O（1），接着又遍历了一次数组，时间复杂度为O（N），因此，这种方法整体的时间复杂度为O（N）。

4.6 如何找出数组中第k小的数

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个整数数组，如何快速地求出该数组中第k小的数。假如数组为{4，0，1，0，2，3}，那么第3小的元素是1。

分析与解答：

由于对一个有序的数组而言，能非常容易地找到数组中第k小的数，因此，可以通过对数组进行排序的方法来找出第k小的数。同时，由于只要求第k小的数，因此，没有必要对数组进行完全排序，只需要对数组进行局部排序就可以了。下面分别介绍这几种不同的实现方法。

方法一：排序法

最简单的方法就是首先对数组进行排序，在排序后的数组中，下标为k-1的值就是第k小的数。例如：对数组{4，0，1，0，2，3}进行排序后的序列变为{0，0，1，2，3，4}，第3小的数就是排序后数组中下标为2对应的数：1。由于最高效的排序算法（例如快速排序）的平均时间复杂度为O（Nlog₂^N），因此，此时该方法的平均时间复杂度为O（Nlog₂^N），其中，N为数组的长度。

方法二：部分排序法

由于只需要找出第k小的数，因此，没必要对数组中所有的元素进行排序，可以采用部分排序的方法。具体思路为：通过对选择排序进行改造，第一次遍历从数组中找出最小的数，第二次遍历从剩下的数中找出最小的数（在整个数组中是第二小的数），第k次遍历就可以从N-k+1（N为数组的长度）个数中找出最小的数（在整个数组中是第k小的）。这种方法的时间复杂度为O（n*k）。当然也可以采用堆排序进行k趟排序找出第k小的值。

方法三：快速排序方法

快速排序的基本思想是：将数组array[low…high]中某一个元素（取第一个元素）作为划分依据，然后把数组划分为三部分：（1）array[low…i-1]（所有的元素的值都小于或等于array[i]）、（2）array[i]、（3）array[i+1…high]（所有的元素的值都大于array[i]）。在此基础上可以用下面的方法求出第k小的元素：

（1）如果i-low==k-1，说明array[i]就是第k小的元素，那么直接返回array[i]。

（2）如果i-low＞k-1，说明第k小的元素肯定在array[low…i-1]中，那么只需要递归地在array[low…i-1]中找第k小的元素即可。

（3）如果i-low＜k-1，说明第k小的元素肯定在array[i+1…high]中，那么只需要递归地在array[i+1…high]中找第k-（i-low）-1小的元素即可。

对于数组{4，0，1，0，2，3}，第一次划分后，划分为下面三部分：

{3，0，1，0，2}，{4}，{}

接下来需要在{3，0，1，0，2}中找第3小的元素，把{3，0，1，0，2}划分为三部分：

{2，0，1，0}，{3}，{}

接下来需要在{2，0，1，0}中找第3小的元素，把{2，0，1，0}划分为三部分：

{0，0，1}，{2}，{}

接下来需要在{0，0，1}中找第3小的元素，把{0，0，1}划分为三部分：

{0}，{0}，{1}

此时i=1，low=0；（i-1=1）＜（k-1=2），接下来需要在{1}中找第k-（i-low）-1=1小的元素即可。显然，{1}中第1小的元素就是1。

实现代码如下：

程序的运行结果如下：

第3小的值为：1

算法性能分析：

快速排序的平均时间复杂度为O（Nlog₂^N）。快速排序需要对划分后的所有子数组继续排序处理，而本方法只需要取划分后的其中一个子数组进行处理即可，因此，平均时间复杂度肯定小于O（Nlog₂^N）。由此可以看出，这种方法的效率要高于方法一。但是这种方法也有缺点：它改变了数组中数据原来的顺序。当然可以申请额外的N（其中，N为数组的长度）个空间来解决这个问题，但是这样做会增加算法的空间复杂度，所以，通常做法是根据实际情况选取合适的方法。

引申：在O（N）时间复杂度内查找数组中前三名

分析与解答：

这道题可以转换为在数组中找出前k大的值（例如，k=3）。

如果没有时间复杂度的要求，可以首先对整个数组进行排序，然后根据数组下标就可以非常容易地找出最大的三个数，即前三名。由于这种方法的效率高低取决于排序算法的效率高低，因此，这种方法在最好的情况下时间复杂度都为O（NlogN）。

通过分析发现，最大的三个数比数组中其他的数都大。因此，可以采用类似求最大值的方法来求前三名，具体实现思路为：初始化前三名（r1：第一名，r2：第二名，r3：第三名）为最小的整数。然后开始遍历数组：

1）如果当前值tmp大于r1：r3=r2，r2=r1，r1=tmp。

2）如果当前值tmp大于r2且不等于r1：r3=r2，r2=tmp。

3）如果当前值tmp大于r3且不等于r2：r3=tmp。

实现代码如下：

程序的运行结果如下：

前三名分别为7，6，5

算法性能分析：

这种方法虽然能够在O（N）的时间复杂度求出前三名，但是当k取值很大的时候，比如求前10名，这种方法就不是很好了。比较经典的方法就是维护一个大小为k的堆来保存最大的k个数，具体思路是：维护一个大小为k的小顶堆用来存储最大的k个数，堆顶保存了最小值，每次遍历一个数m，如果m比堆顶元素小，那么说明m肯定不是最大的k个数，因此，不需要调整堆，如果m比堆顶元素大，则用这个数替换堆顶元素，替换后重新调整堆为小顶堆。这种方法的时间复杂度为O（N*logk）。这种方法适用于数据量大的情况。

4.7 如何求数组中两个元素的最小距离

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个数组，数组中含有重复元素，给定两个数字num1和num2，求这两个数字在数组中出现的位置的最小距离。

分析与解答：

对于这类问题，最简单的方法就是对数组进行双重遍历，找出最小距离，但是这种方法效率比较低下。由于在求距离的时候只关心num1与num2这两个数，因此，只需要对数组进行一次遍历即可，在遍历的过程中分别记录遍历到num1或num2的位置就可以非常方便地求出最小距离，下面分别详细介绍这两种实现方法。

方法一：蛮力法

主要思路是：对数组进行双重遍历，外层循环遍历查找num1，只要遍历到num1，内层循环对数组从头开始遍历找num2，每当遍历到num2，就计算它们的距离dist。当遍历结束后最小的dist值就是它们最小的距离。实现代码如下：

程序的运行结果如下：

2

算法性能分析：

这种方法需要对数组进行两次遍历，因此，时间复杂度为O（n^2）。

方法二：动态规划

上述方法的内层循环对num2的位置进行了很多次重复的查找。可以采用动态规划的方法把每次遍历的结果都记录下来从而减少遍历次数。具体实现思路是：遍历数组，会遇到以下两种情况：

（1）当遇到num1时，记录下num1值对应的数组下标的位置lastPos1，通过求lastPos1与上次遍历到num2下标的位置的值lastPos2的差可以求出最近一次遍历到的num1与num2的距离。

（2）当遇到num2时，同样记录下它在数组中下标的位置lastPos2，然后通过求lastPos2与上次遍历到num1的下标值lastPos1，求出最近一次遍历到的num1与num2的距离。

假设给定数组为：{4，5，6，4，7，4，6，4，7，8，5，6，4，3，10，8}，num1=4，num2=8。根据以上方法，执行过程如下：

1）在遍历的时候首先会遍历到4，下标为lastPos1=0，由于此时还没有遍历到num2，因此，没必要计算num1与num2的最小距离。

2）接着往下遍历，又遍历到num1=4，更新lastPos1=3。

3）接着往下遍历，又遍历到num1=4，更新lastPos1=7。

4）接着往下遍历，又遍历到num2=8，更新lastPos2=9；此时由于前面已经遍历到过num1，因此，可以求出当前num1与num2的最小距离为|lastPos2-lastPos1|=2。

5）接着往下遍历，又遍历到num2=8，更新lastPos2=15；此时由于前面已经遍历到过num1，因此，可以求出当前num1与num2的最小距离为|lastPos2-lastPos1|=8；由于8＞2，所以，num1与num2的最小距离为2。

实现代码如下：

算法性能分析：

这种方法只需要对数组进行一次遍历，因此，时间复杂度为O（N）。

4.8 如何求解最小三元组距离

【出自GG面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

已知三个升序整数数组a[l]、b[m]和c[n]，请在三个数组中各找一个元素，使得组成的三元组距离最小。三元组距离的定义是：假设a[i]、b[j]和c[k]是一个三元组，那么距离为Distance=max（|a[i]-b[j]|，|a[i]-c[k]|，|b[j]-c[k]|），请设计一个求最小三元组距离的最优算法。

分析与解答：

最简单的方法就是找出所有可能的组合，从所有的组合中找出最小的距离，但是显然这种方法的效率比较低下。通过分析发现，当a_i≤b_i≤c_i时，此时它们的距离肯定为D_i=c_i-a_i。此时就没必要求b_i-a_i与c_i-ai的值了，从而可以省去很多不必要的步骤，下面分别详细介绍这两种方法。

方法一：蛮力法

最容易想到的方法就是分别遍历三个数组中的元素，对遍历到的元素分别求出它们的距离，然后从这些值里面查找最小值，实现代码如下：

程序的运行结果如下：

最小距离为：5

算法性能分析：

这种方法的时间复杂度为O（l*m*n），显然这种方法没有用到数组升序这一特性，因此，该方法肯定不是最好的方法。

方法二：最小距离法

假设当前遍历到这三个数组中的元素分别为a_i、b_i和c_i，并且a_i≤b_i≤c_i，此时它们的距离肯定为D_i=c_i-a_i，那么接下来可以分如下三种情况讨论：

（1）如果接下来求a_i、b_i、c_i+1的距离，由于c_i+1≥c_i，此时它们的距离必定为D_i+1=c_i+1-a_i，显然D_i+1≥D_i，因此，D_i+1不可能为最小距离。

（2）如果接下来求a_i、b_i+1、c_i的距离，由于b_i+1≤b_i，如果b_i+1≤c_i，此时它们的距离仍然为D_i+1=c_i-a_i；如果b_i+1＞c_i，那么此时它们的距离为D_i+1=b_i+1-a_i，显然D_i+1≥D_i，因此，D_i+1不可能为最小距离。

（3）如果接下来求a_i+1、b_i、c_i的距离，如果a_i+1＜c_i-|c_i-a_i|，此时它们的距离D_i+1=max（c_i-a_i+1，c_i-b_i），显然D_i+1＜D_i，因此，D_i+1有可能是最小距离。

综上所述，在求最小距离的时候只需要考虑第3种情况即可。具体实现思路是：从三个数组的第一个元素开始，首先求出它们的距离minDist，接着找出这三个数中最小数所在的数组，只对这个数组的下标往后移一个位置，接着求三个数组中当前遍历元素的距离，如果比minDist小，则把当前距离赋值给minDist，依此类推，直到遍历完其中一个数组为止。

例如给定数组：a[]={3，4，5，7，15}；b[]={10，12，14，16，17}；c[]={20，21，23，24，37，30}。

1）首先从三个数组中找出第一个元素3、10、20，显然它们的距离为20-3=17。

2）由于3最小，因此，数组a往后移一个位置，求4、10、20的距离为16，由于16＜17，因此，当前数组的最小距离为16。

3）同理，对数组a后移一个位置，依次类推直到遍历到15的时候，当前遍历到三个数组中的值分别为15、10、20，最小距离为10。

4）由于10最小，因此，数组b往后移动一个位置遍历12，此时三个数组遍历到的数字分别为15、12、20，距离为8，当前最小距离是8。

5）由于8最小，数组b往后移动一个位置为14，依然是三个数中最小值，往后移动一个位置为16，当前的最小距离变为5，由于15是数组a的最后一个数字，因此，遍历结束，求得最小距离为5。

实现代码如下：

算法性能分析：

采用这种算法最多只需要对三个数组分别遍历一遍，因此，时间复杂度为O（l+m+n）。

方法三：数学运算法

采用数学方法对目标函数变形，有两个关键点，第一个关键点：

max{|x1-x2|，|y1-y2|}=（|x1+y1-x2-y2|+|x1-y1-（x2-y2）|）/2 公式（1）

假设x1=a[i]，x2=b[j]，x3=c[k]，则

Distance=max（|x1-x2|，|x1-x3|，|x2-x3|）=max（max（|x1-x2|，|x1-x3|），|x2-x3|） 公式（2）

根据公式（1），max（|x1-x2|，|x1-x3|）=1/2（|2x1-x2-x3|+|x2-x3|），带入公式（2），得到

Distance=max（1/2（|2x1-x2-x3|+|x2-x3|），|x2-x3|）=1/2*max（|2x1-x2-x3|，|x2-x3|）+1/2*|x2-x3|//把相同部分1/2*|x2-x3|分离出来

=1/2*max（|2x1-（x2+x3）|，|x2-x3|）+1/2*|x2-x3|//把（x2+x3）看成一个整体，使用公式（1）

=1/2*1/2*（（|2x1-2x2|+|2x1-2x3|）+1/2*|x2-x3|

=1/2*|x1-x2|+1/2*|x1-x3|+1/2*|x2-x3|

=1/2*（|x1-x2|+|x1-x3|+|x2-x3|）//求出等价公式，完毕！

第二个关键点：如何设计算法找到（|x1-x2|+|x1-x3|+|x2-x3|）的最小值，x1、x2、x3分别是三个数组中的任意一个数，算法思想与方法二相同，用三个下标分别指向a、b、c中最小的数，计算一次它们最大距离的Distance，然后再移动三个数中较小的数组的下标，再计算一次，每次移动一个，直到其中一个数组结束为止。

示例代码如下：

程序的运行结果如下：

最小距离为：5

算法性能分析：

与方法二类似，这种方法最多需要执行（l+m+n）次循环，因此，时间复杂度为O（l+m+n）。

4.9 如何求数组中绝对值最小的数

【出自MT面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

有一个升序排列的数组，数组中可能有正数、负数或0，求数组中元素的绝对值最小的数。例如，数组{-10，-5，-2，7，15，50}，该数组中绝对值最小的数是-2。

分析与解答：

可以对数组进行顺序遍历，对每个遍历到的数求绝对值进行比较就可以很容易地找出数组中绝对值最小的数。本题中，由于数组是升序排列的，那么绝对值最小的数一定在正数与非正数的分界点处，利用这种方法可以省去很多求绝对值的操作。下面分别详细介绍这几种方法。

方法一：顺序比较法

最简单的方法就是从头到尾遍历数组元素，对每个数字求绝对值，然后通过比较就可以找出绝对值最小的数。

以数组{-10，-5，-2，7，15，50}为例，实现方式如下：

（1）首先遍历第一个元素-10，其绝对值为10，所以，当前最小值为min=10。

（2）遍历第二个元素-5，其绝对值为5，由于5＜10，因此，当前最小值min=5。

（3）遍历第三个元素-2，其绝对值为2，由于2＜5，因此，当前最小值为min=2。

（4）遍历第四个元素7，其绝对值为7，由于7＞2，因此，当前最小值min还是2。

（5）依此类推，直到遍历完数组为止就可以找出绝对值最小的数为-2。

示例代码如下：

程序的运行结果如下：

绝对值最小的数为：-2

算法性能分析：

该方法的平均时间复杂度为O（N），空间复杂度为O（1）。

方法二：二分法

在求绝对值最小的数时可以分为如下三种情况：（1）如果数组第一个元素为非负数，那么绝对值最小的数肯定为数组第一个元素。（2）如果数组最后一个元素的值为负数，那么绝对值最小的数肯定是数组的最后一个元素。（3）如果数组中既有正数又有负数，首先找到正数与负数的分界点，如果分界点恰好为0，那么0就是绝对值最小的数。否则通过比较分界点左右的正数与负数的绝对值来确定最小的数。

那么如何来查找正数与负数的分界点呢？最简单的方法仍然是顺序遍历数组，找出第一个非负数（前提是数组中既有正数又有负数），接着通过比较分界点左右两个数的值来找出绝对值最小的数。这种方法在最坏的情况下时间复杂度为O（N）。下面主要介绍采用二分法来查找正数与负数的分界点的方法。主要思路是：取数组中间位置的值a[mid]，并将它与0值比较，比较结果分为以下3种情况：

（1）如果a[mid]==0，那么这个数就是绝对值最小的数。

（2）如果a[mid]＞0，a[mid-1]＜0，那么就找到了分界点，通过比较a[mid]与a[mid-1]的绝对值就可以找到数组中绝对值最小的数；如果a[mid-1]==0，那么a[mid-1]就是要找的数；否则接着在数组的左半部分查找。

（3）如果a[mid]＜0，a[mid+1]＞0，那么通过比较a[mid]与a[mid+1]的绝对值即可；如果a[mid+1]==0，那么a[mid+1]就是要查找的数。否则接着在数组的右半部分继续查找。

为了更好地说明以上方法，可以参考以下几个示例进行分析：

（1）如果数组为{1，2，3，4，5，6，7}，由于数组元素全部为正数，而且数组是升序排列，所以，此时绝对值最小的元素为数组的第一个元素1。

（2）如果数组为{-7，-6，-5，-4，-3，-2，-1}，此时数组长度length的值为7，由于数组元素全部为负数，而且数组是升序排列，所以，此时绝对值最小的元素为数组的第length-1个元素，该元素的绝对值为1。

（3）如果数组为{-7，-6，-5，-3，-1，2，4，}，此时数组长度length为7，数组中既有正数，也有负数，此时采用二分查找法，判断数组中间元素的符号。中间元素的值为-3，小于0，所以，判断中间元素后面一个元素的符号，中间元素后面的元素的值为-1小于0，因此，绝对值最小的元素一定位于右半部份数组{-1，2，4}中，继续在右半部分数组中查找，中间元素为2大于0，2前面一个元素的值为-1小于0，所以，-1与2中绝对值最小的元素即为所求的数组的绝对值最小的元素的值，所以，数组中绝对值最小的元素的值为-1。

实现代码如下：

算法性能分析：

通过上面的分析可知，由于采取了二分查找的方式，算法的平均时间复杂度得到了大幅降低，为O（log₂^N），其中，N为数组的长度。

4.10 如何求数组连续最大和

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

一个有n个元素的数组，这n个元素既可以是正数也可以是负数，数组中连续的一个或多个元素可以组成一个连续的子数组，一个数组可能有多个这种连续的子数组，求子数组和的最大值。例如：对于数组{1，-2，4，8，-4，7，-1，-5}而言，其最大和的子数组为{4，8，-4，7}，最大值为15。

分析与解答：

这是一道在笔试面试中碰到的非常经典的算法题，有多种解决方法，下面分别从简单到复杂逐个介绍各种方法。

方法一：蛮力法

最简单也是最容易想到的方法就是找出所有的子数组，然后求出子数组的和，在所有子数组的和中取最大值。实现代码如下：

程序的运行结果如下：

连续最大和为：15

算法性能分析：

这种方法的时间复杂度为O（n^3），显然效率太低，通过对该方法进行分析发现，许多子数组都重复计算了，鉴于此，下面给出一种优化的方法。

方法二：重复利用已经计算的子数组和

由于Sum[i，j]=Sum[i，j-1]+arr[j]，在计算Sum[i，j]的时候可以使用前面已计算出的Sum[i，j-1]而不需要重新计算，采用这种方法可以省去计算Sum[i，j-1]的时间，因此，可以提高程序的效率。

实现代码如下：

算法性能分析：

这种方法使用了双重循环，因此，时间复杂度为O（n^2）。

方法三：动态规划方法

可以采用动态规划的方法来降低算法的时间复杂度。实现思路如下。

首先可以根据数组的最后一个元素arr[n-1]与最大子数组的关系分为以下三种情况讨论：

（1）最大子数组包含arr[n-1]，即最大子数组以arr[n-1]结尾。

（2）arr[n-1]单独构成最大子数组。

（3）最大子数组不包含arr[n-1]，那么求arr[1…n-1]的最大子数组可以转换为求arr[1…n-2]的最大子数组。

通过上述分析可以得出如下结论：假设已经计算出子数组arr[1…i-2]的最大的子数组和All[i-2]，同时也计算出arr[0…i-1]中包含arr[i-1]的最大的子数组和为End[i-1]。则可以得出如下关系：All[i-1]=max{End[i-1]，arr[i-1]，All[i-2]}。利用这个公式和动态规划的思想可以得到如下代码：

算法性能分析：

与前面几个方法相比，这种方法的时间复杂度为O（N），显然效率更高，但是由于在计算的过程中额外申请了两个数组，因此，该方法的空间复杂度也为O（N）。

方法四：优化的动态规划方法

方法三中每次其实只用到了End[i-1]与All[i-1]，而不是整个数组中的值，因此，可以定义两个变量来保存End[i-1]与All[i-1]的值，并且可以反复利用。实现代码如下：

算法性能分析：

这种方法在保证了时间复杂度为O（N）的基础上，把算法的空间复杂度也降到了O（1）。

引申：在知道子数组最大值后，如何才能确定最大子数组的位置？

分析与解答：

为了得到最大子数组的位置，首先介绍另外一种计算最大子数组和的方法。在上例的方法三中，通过对公式End[i]=max（End[i-1]+arr[i]，arr[i]）的分析可以看出，当End[i-1]＜0时，End[i]=array[i]，其中End[i]表示包含array[i]的子数组和，如果某一个值使得End[i-1]＜0，那么就从arr[i]重新开始。可以利用这个性质非常容易地确定最大子数组的位置。

实现代码如下：

程序的运行结果如下：

连续最大和为：15

最大和对应的数组起始与结束坐标分别为：2，5

4.11 如何找出数组中出现1次的数

【出自XM笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

一个数组里，除了三个数是唯一出现的，其余的数都出现偶数次，找出这三个数中的任意一个。比如数组序列为{1，2，4，5，6，4，2}，只有1，5，6这三个数字是唯一出现的，数字2与4均出现了偶数次（2次），只需要输出数字1、5、6中的任意一个就行。

分析与解答：

根据题目描述可以得到如下几个有用的信息：

（1）数组中元素个数一定是奇数个。

（2）由于只有三个数字出现过一次，显然这三个数字不相同，因此，这三个数对应的二进制数也不可能完全相同。

由此可知，必定能找到二进制数中的某一个bit来区分这三个数（这一个bit的取值或者为0，或者为1），当通过这一个bit的值对数组进行分组的时候，这三个数一定可以被分到两个子数组中，并且其中一个子数组中分配了两个数字，而另一个子数组分配了一个数字，而其他出现两次的数字肯定是成对出现在子数组中的。此时只需要重点关注哪个子数组中分配了这三个数中的其中一个，就可以很容易地找出这个数字了。当数组被分成两个子数组时，这一个bit的值为1的数被分到一个子数组subArray1，这一个bit的值为0的数被分到另外一个子数组subArray0。

（1）如果subArray1中元素个数为奇数个，那么对subArray1中的所有数字进行异或操作；由于a^a=0，a^0=a，出现两次的数字通过异或操作得到的结果为0，然后再与只出现一次的数字执行异或操作，得到的结果就是只出现一次的数字。

（2）如果subArray0中元素个数为奇数个，那么对subArray0中所有元素进行异或操作得到的结果就是其中一个只出现一次的数字。

为了实现上面的思路，必须先找到能区分这三个数字的位，根据以上的分析给出本算法的实现思路：

以32位平台为例，一个int类型的数字占用32位空间，从右向左使用每一位对数组进行分组，分组的过程中，计算这个位值为0的数字异或的结果result0，出现的次数count0；这个位值为1的所有数字异或的结果result1，出现的次数count1。

如果count0是奇数且result1！=0，那么说明这三个数中的其中一个被分配到这一位为0的子数组中了，因此，这个子数组中所有数字异或的值result0^一定是出现一次的数字。（如果result1==0，说明这一个位不能用来区分这三个数字，此时这三个数字都被分配到子数组subArray0中了，因此，result1！=0就可以确定这一个位可以被用来区分这三个数字的）。

同理，如果count1是奇数且result0！=0，那么result1就是其中一个出现1次的数。

以{6，3，4，5，9，4，3}为例，出现1次的数字为6（110），5（101），9（1001），从右向左第一位就可以区分这三个数字，用这个位可以把数字分成两个子数组subArray0={6，4，4}和subArray1={3，5，9，3}。subArray1中所有元素异或的值不等于0，说明出现1次的数字一定在subArray1中出现了，而subArray0中元素个数为奇数个，说明出现1次的数字，其中只有一个被分配到subArray0中了，所以，subArray0中所有元素异或的结果一定就是这个出现1次的数字6。实现代码如下：

程序的运行结果如下：

6

算法性能分析：

这种方法使用了两层循环，总共循环执行的次数为32*N（N为数组的长度），因此，算法的时间复杂度为O（N）。

4.12 如何对数组旋转

【出自MT笔试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

请实现方法：print_rotate_matrix（intmatrix，intn），该方法用于将一个n*n的二维数组逆时针旋转45°后打印，例如，下图显示一个3*3的二维数组及其旋转后屏幕输出的效果。

分析与解答：

本题的思路：从右上角开始对数组中的元素进行输出，实现代码如下：

程序的运行结果如下：

3

2 6

1 5 9

4 8

7

算法性能分析：

这种方法对数组中的每个元素都遍历了一次，因此，算法的时间复杂度为O（n^2）。

4.13 如何在不排序的情况下求数组中的中位数

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

所谓中位数就是一组数据从小到大排列后中间的那个数字。如果数组长度为偶数，那么中位数的值就是中间两个数字相加除以2；如果数组长度为奇数，那么中位数的值就是中间那个数字。

分析与解答：

根据定义，如果数组是一个已经排序好的数组，那么直接通过索引即可获取到所需的中位数。如果题目允许排序的话，那么本题的关键在于选取一个合适的排序算法对数组进行排序。一般而言，快速排序的平均时间复杂度较低，为O（NlogN），所以，如果采用排序方法的话，算法的平均时间复杂度为O（NlogN）。

可是，题目要求不许使用排序算法。那么前一种方法显然走不通。此时，可以换一种思路：分治的思想。快速排序算法在每一次局部递归后都保证某个元素左侧的元素的值都比它小，右侧的元素的值都比它大，因此，可以利用这个思路快速地找到第N大元素，而与快速排序算法不同的是，这种方法关注的并不是元素的左右两边，而仅仅是某一边。

根据快速排序的方法，可以采用一种类似快速排序的方法，找出这个中位数。具体而言，首先把问题转化为求一列数中第i小的数的问题，求中位数就是求一列数的第（length/2+1）小的数的问题（其中length表示的是数组序列的长度）。

当使用一次类快速排序算法后，分割元素的下标为pos：

（1）当pos＞length/2时，说明中位数在数组左半部分，那么继续在左半部分查找。

（2）当pos==lengh/2时，说明找到该中位数，返回A[pos]即可。

（3）当pos＜length/2时，说明中位数在数组右半部分，那么继续在数组右半部分查找。

以上默认此数组序列长度为奇数，如果为偶数就是调用上述方法两次找到中间的两个数求平均值。示例代码如下：

程序的运行结果如下：

6

算法性能分析：

这种方法在平均情况下的时间复杂度为O（N）。

4.14 如何求集合的所有子集

【出自TX笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

有一个集合，求其全部子集（包含集合自身）。给定一个集合s，它包含两个元素＜a，b＞，则其全部的子集为＜a，ab，b＞。

分析与解答：

根据数学性质分析，不难得知，子集个数Sn与原集合元素个数n之间的关系满足如下等式：Sn=2^n-1。

方法一：位图法

具体步骤如下所示。

（1）构造一个和集合一样大小的数组A，分别与集合中的某个元素对应，数组A中的元素只有两种状态：“1”和“0”，分别代表每次子集输出中集合中对应元素是否要输出，这样数组A可以看作是原集合的一个标记位图。

（2）数组A模拟整数“加1”的操作，每执行“加1”操作之后，就将原集合中所有与数组A中值为“1”的相对应的元素输出。

设原集合为＜a，b，c，d＞，数组A的某次“加1”后的状态为[1，0，1，1]，则本次输出的子集为＜a，c，d＞。使用非递归的思想，如果有一个数组，大小为n，那么就使用n位的二进制。如果对应的位为1，那么就输出这个位；如果对应的位为0，那么就不输出这个位。

例如集合{a，b，c}的所有子集可表示如下：

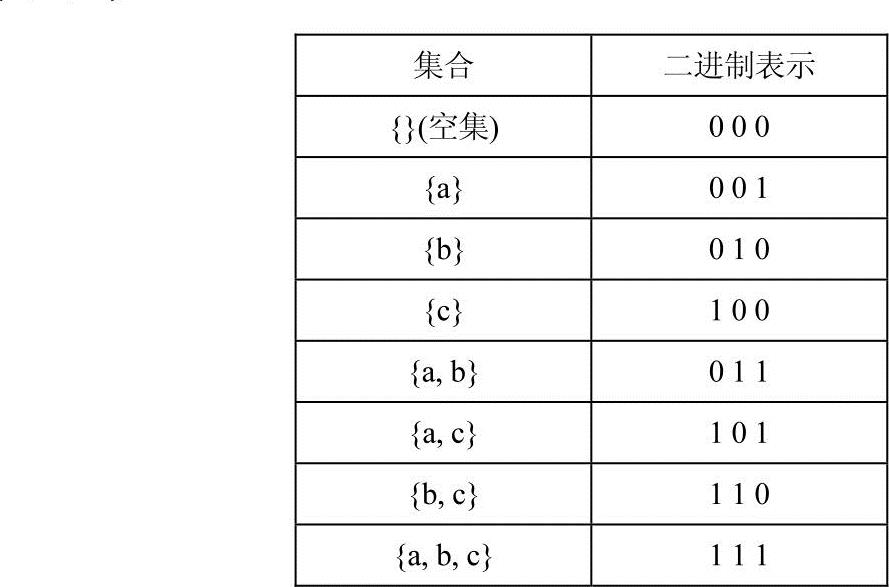
算法的重点是模拟数组加1的操作。数组可以一直加1，直到数组内所有元素都是1。实现代码如下：

程序的运行结果如下：

{abc}

{ab}

{ac}

{a}

{bc}

{b}

{c}

{}

该方法的缺点在于如果数组中有重复数时，这种方法将会得到重复的子集。

算法性能分析：

这种方法的时间复杂度为O（N*2^N），空间复杂度O（N）。

方法二：迭代法

1）采用迭代算法的具体过程如下：

假设原始集合s=＜a，b，c，d＞，子集结果为r：

第一次迭代：

r=＜a＞

第二次迭代：

r=＜aabb＞

第三次迭代：

r=＜aabbacabcbcc＞

第四次迭代：

r=＜aabbacabcbccadabdbdacdabcdbcdcdd＞

每次迭代，都是上一次迭代的结果+上次迭代结果中每个元素都加上当前迭代的元素+当前迭代的元素。

代码中使用到了vector容器。这个容器记录了这次迭代需要输出的集合，使用容器的目的是为了这次迭代的时候可以参考上次输出的结果。实现代码如下：

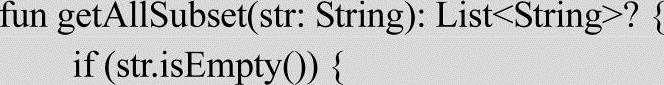
程序的运行结果如下：

a

ab

b

ac

abc

bc

c

根据上述过程可知，第k次迭代的迭代次数为2^k-1。需要注意的是，n＞=k＞=1，迭代n次，总的遍历次数为2^（n+1）-（2+n），n＞=1，所以，本方法的时间复杂度为O（2^n）。

由于在该算法中，下一次迭代过程都需要上一次迭代的结果，而最后一次迭代之后就没有下一次了。因此，假设原始集合有n个元素，则在迭代过程中，总共需要保存的子集个数为2^（n-1）-1，n＞=1。但需要注意的是，这里只考虑了子集的个数，每个子集元素的长度都被视为1。

其实，比较上述两种方法，不难发现，第一种方法可以看作是用时间换空间，而第二种方法可以看作是用空间换时间。

4.15 如何对数组进行循环移位

【出自TX面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

把一个含有N个元素的数组循环右移K（K是正数）位，要求时间复杂度为O（N），且只允许使用两个附加变量。

分析与解答：

由于有空间复杂度的要求，因此，只能在原数组中就地进行右移。

方法一：蛮力法

蛮力法是最简单的方法，题目中需要将数组元素循环右移K位，只需要每次将数组中的元素右移一位，循环K次即可。例如，假设原数组为abcd1234，那么，按照此种方式，具体移动过程如下所示：abcd1234→4abcd123→34abcd12→234abcd1→1234abcd。

此种方法也很容易写出代码。示例代码如下：

程序的运行结果如下：

5 6 7 8 1 2 3 4

以上方法虽然可以实现数组的循环右移，但是由于每移动一次，其时间复杂度就为O（N），所以，移动K次，其总的时间复杂度为O（K*N），0＜K＜N，与题目要求的O（N）不符合，需要继续往下探索。

对于上述代码需要考虑到，K不一定小于N，有可能等于N，也有可能大于N。当K＞N时，右移K-N之后的数组序列跟右移K位的结果一样，所以，当K＞N时，右移K位与右移K′（其中K′=K%N）位等价，根据以上分析，相对完备的代码如下：

算法性能分析：

上例中，算法的时间复杂度为O（N²），与K值无关，但时间复杂度仍然太高，是否还有其他更好的方法呢？

仔细分析上面的方法，不难发现，上述方法的移动采取的是一步一步移动的方式，可是问题是，题目中已经告知了需要移动的位数为K，为什么不能一步到位呢？

方法二：空间换时间法

通常情况下，以空间换时间往往能够降低时间复杂度，本题也不例外。

首先定义一个辅助数组T，把数组A的第N-K+1到N位数组中的元素存储到辅助数组T中，再把数组A中的第1到N-K位数组元素存储到辅助数组T中，然后将数组T中的元素复制回数组A，这样就完成了数组的循环右移，此时的时间复杂度为O（N）。

虽然时间复杂度满足要求，但是空间复杂度却提高了。由于需要创建一个新的数组，所以，此时的空间复杂度为O（N），鉴于此，还可以对此方法继续优化。

方法三：翻转法

把数组看成由两段组成的，记为XY。左旋转相当于要把数组XY变成YX。先在数组上定义一种翻转的操作，就是翻转数组中数字的先后顺序。把X翻转后记为X^T。显然有（X^T）^T=X。

首先对X和Y两段分别进行翻转操作，这样就能得到X^TY^T。接着再对X^TY^T进行翻转操作，得到（X^TY^T）^T=（Y^T）^T（X^T）^T=YX。正好是期待的结果。

回到原来的题目。要做的仅仅是把数组分成两段，再定义一个翻转子数组的函数，按照前面的步骤翻转三次就行了。时间复杂度和空间复杂度都合乎要求。

对于数组序列A={123456}，如何实现对其循环右移2位的功能呢？将数组A分成两个部分：A[0～N-K-1]和A[N-K～N-1]，将这两个部分分别翻转，然后放在一起再翻转（反序）。具体如下：

（1）翻转1234：123456---＞432156

（2）翻转56：432156---＞432165

（3）翻转432165：432165---＞561234

示例代码如下：

算法性能分析：

此时的时间复杂度为O（N）。主要是完成翻转（逆序）操作，并且只用了一个辅助空间。

引申：上述问题中K不一定为正整数，有可能为负整数。当K为负整数的时候，右移K位，可以理解为左移（-K）位，所以，此时可以将其转换为能够求解的情况。

4.16 如何在有规律的二维数组中进行高效的数据查找

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请实现一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

例如下面的二维数组就是符合这种约束条件的。如果在这个数组中查找数字7，由于数组中含有该数字，则返回true；如果在这个数组中查找数字5，由于数组中不含有该数字，则返回false。

1

分析与解答：

最简单的方法就是对二维数组进行顺序遍历，然后判断待查找元素是否在数组中，这种方法的时间复杂度为O（M*N），其中，M、N分别为二维数组的行数和列数。

虽然上述方法能够解决问题，但这种方法显然没有用到二维数组中数组元素有序的特点，因此，该方法肯定不是最好的方法。

此时需要转换一种思路进行思考，一般情况下，当数组中元素有序的时候，二分查找是一个很好的方法，对于本题而言，同样适用二分查找，实现思路如下：

给定数组array（行数：rows，列数：columns，待查找元素：data），首先，遍历数组右上角的元素（i=0，j=columns-1），如果array[i][j]==data，则在二维数组中找到了data，直接返回；如果array[i][j]＞data，则说明这一列其他的数字也一定大于data，因此，没有必要在这一列继续查找了，通过j--操作排除这一列。同理，如果array[i][j]＜data，则说明这一行中其他数字也一定比data小，因此，没有必要再遍历这一行了，可以通过i++操作排除这一行。依次类推，直到遍历完数组结束。

实现代码如下：

程序的运行结果如下：

false

true

算法性能分析：

这种方法主要从二维数组的右上角遍历到左下角，因此，算法的时间复杂度为O（M+N），此外，这种方法没有申请额外的存储空间。

4.17 如何寻找最多的覆盖点

【出自BD笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

坐标轴上从左到右依次的点为a[0]、a[1]、a[2]…a[n-1]，设一根木棒的长度为L，求L最多能覆盖坐标轴的几个点？

分析与解答：

本题求满足a[j]-a[i]＜=L&&a[j+1]-a[i]＞L这两个条件的j与i中间的所有点个数中的最大值，即j-i+1最大，这样题目就简单多了，方法也很简单：直接从左到右扫描，使用两个索引i和j，i从位置0开始，j从位置1开始，如果a[j]-a[i]＜=L，则j++前进，并记录中间经过的点的个数，如果a[j]-a[i]＞L，则j--回退，覆盖点个数-1，回到刚好满足条件的时候，将满足条件的最大值与前面找出的最大值比较，记录下当前的最大值，然后执行i++、j++，直到求出最大的点个数。

有两点需要注意，如下所示：

（1）这里可能不存在i和j使得a[j]-a[i]刚好等于L的情况发生，所以，判断条件不能为a[j]-a[i]==L。

（2）可能存在不同的覆盖点但覆盖的长度相同的情况发生，此时只选取第一次覆盖的点。

实现代码如下：

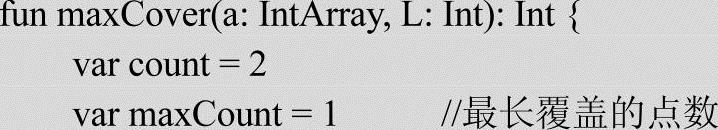
程序的运行结果如下：

覆盖的坐标点：7 8 10 11 12 13 15

最长覆盖点数：7

算法性能分析：

这种方法的时间复杂度为O（N），其中，N为数组的长度。

4.18 如何判断请求能否在给定的存储条件下完成

【出自BD笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一台有m个存储空间的机器，有n个请求需要在这台机器上运行，第i个请求计算时需要占R[i]空间，计算结果需要占O[i]个空间（O[i]＜R[i]）。请设计一个算法，判断这n个请求能否全部完成？若能，给出这n个请求的安排顺序。

分析与解答：

这道题的主要思路是：首先对请求按照R[i]-O[i]由大到小进行排序，然后按照由大到小的顺序进行处理，如果按照这个顺序能处理完，则这n个请求能被处理完，否则处理不完。那么请求i能完成的条件是什么呢？在处理请求i的时候前面所有的请求都已经处理完成，那么它们所占的存储空间为O（0）+O（1）+…+O（i-1），那么剩余的存储空间left为left=m-（O（0）+O（1）+…+O（i-1）），要使请求i能被处理，则必须满足left＞=R[i]，只要剩余的存储空间能存放的下R[i]，那么在请求处理完成后就可以删除请求，从而把处理的结果放到存储空间中。由于O[i]＜R[i]，此时必定有空间存放O[i]。

至于为什么用R[i]-O[i]由大到小的顺序来处理，请看下面的分析：

假设第一步处理R[i]-O[i]最大的值。使用归纳法（假设每一步都取剩余请求中R[i]-O[i]最大的值进行处理），假设n=k时能处理完成，那么当n=k+1时，由于前k个请求是按照R[i]-O[i]从大到小排序的，在处理第k+1个请求时，此时需要的空间为A=O[1]+…+O[i]+…+O[k]+R[k+1]，只有A＜=m的时候才能处理第k+1个请求。假设把第k+1个请求和前面的某个请求i换换位置，即不按照R[i]-O[i]由大到小的顺序来处理，在这种情况下，第k+1个请求已经被处理完成，接着要处理第i个请求，此时需要的空间为B=O[1]+…+O[i-1]+O[k+1]+O[i+1]+…+R[i]，如果B＞A，则说明按顺序处理成功的可能性更大（越往后处理剩余的空间越小，请求需要的空间越小越好）；如果B＜A，则说明不按顺序更好。根据R[i]-O[i]有序的特点可知：R[i]-O[i]＞=R[k+1]-O[k+1]，即O[k+1]+R[i]＞=O[i]+R[k+1]，所以，B＞=A，因此，可以得出结论：方案B不会比方案A更好。即方案A是最好的方案，也就是说，按照R[i]-O[i]从大到小排序处理请求，成功的可能性最大。如果按照这个序列都无法完成请求序列，那么任何顺序都无法实现全部完成，实现代码如下：

程序的运行结果如下：

按照如下请求序列可以完成：

20，423，810，215，716，86，59，87，6

算法性能分析：

这种方法的时间复杂度为O（N^2）。

4.19 如何按要求构造新的数组

【出自BD笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个数组a[N]，希望构造一个新的数组b[N]，其中，b[i]=a[0]*a[1]*…*a[N-1]/a[i]。在构造数组的过程中，有如下几点要求：

（1）不允许使用除法。

（2）要求O（1）空间复杂度和O（N）时间复杂度。

（3）除遍历计数器与a[N]、b[N]外，不可以使用新的变量（包括栈临时变量、堆空间和全局静态变量等）。

（4）请用程序实现并简单描述。

分析与解答：

如果没有时间复杂度与空间复杂度的要求，算法将非常简单。首先遍历一遍数组a，计算数组a中所有元素的乘积，并保存到一个临时变量tmp中，然后再遍历一遍数组a并给数组赋值：b[i]=tmp/a[i]，但是这种方法使用了一个临时变量，因此，不满足题目的要求。下面介绍另外一种方法。

在计算b[i]的时候，只要将数组a中除了a[i]以外的所有值相乘即可。这种方法的主要思路是：首先遍历一遍数组a，在遍历的过程中对数组b进行赋值：b[i]=a[i-1]*b[i-1]，这样经过一次遍历后，数组b的值为b[i]=a[0]*a[1]*…*a[i-1]。此时只需要将数组中的值b[i]再乘以a[i+1]*a[i+2]*…a[N-1]，实现方法为逆向遍历数组a，把数组后半段值的乘积记录到b[0]中，通过b[i]与b[0]的乘积就可以得到满足题目要求的b[i]，具体而言，执行b[i]=b[i]*b[0]（首先执行的目的是为了保证在执行下面一个计算的时候，b[0]中不包含与b[i]的乘积），接着记录数组后半段的乘积到b[0]中：b[0]*=b[0]*a[i]。

实现代码如下：

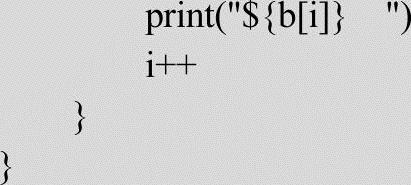
程序的运行结果如下：3628800 1814400 1209600 907200 725760 604800 518400 453600 403200 362880

4.20 如何获取最好的矩阵链相乘方法

【出自XM面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个矩阵序列，找到最有效的方式将这些矩阵相乘在一起。给定表示矩阵链的数组p[]，使得第i个矩阵Ai的维数为p[i-1]×p[i]。编写一个函数MatrixChainOrder（），该函数应该返回乘法运算所需的最小乘法数。

输入：p[]={40，20，30，10，30}

输出：26000

有4个大小为40×20、20×30、30×10和10×30的矩阵。假设这四个矩阵为A、B、C和D，该函数的执行方法可以使执行乘法运算的次数最少。

分析与解答：

该问题实际上并不是执行乘法，而只是决定以哪个顺序执行乘法。由于矩阵乘法是关联的，所以有很多选择来进行矩阵链的乘法运算。换句话说，无论采用哪种方法来执行乘法，结果将是一样的。例如，如果有四个矩阵A、B、C和D，可以有如下几种执行乘法的方法：

（ABC）D=（AB）（CD）=A（BCD）=…

虽然这些方法的计算结果相同。但是，不同的方法需要执行乘法的次数是不相同的，因此效率也是不同的。例如，假设A是10×30矩阵，B是30×5矩阵，C是5×60矩阵。那么，

（AB）C的执行乘法运算的次数为（10×30×5）+（10×5×60）=1500+3000=4500次。

A（BC）的执行乘法运算的次数为（30×5×60）+（10×30×60）=9000+18000=27000次。

显然，第一种方法需要执行更少的乘法运算，因此效率更高。

对于本题中示例而言，执行乘法运算的次数最少的方法如下：

（A（BC））D的执行乘法运算的次数为20*30*10+40*20*10+40*10*30。

方法一：递归法

最简单的方法就是在所有可能的位置放置括号，计算每个放置的成本并返回最小值。在大小为n的矩阵链中，可以以n-1种方式放置第一组括号。例如，如果给定的链是4个矩阵。（A）（BCD）、（AB）（CD）和（ABC）（D）中，有三种方式放置第一组括号。每个括号内的矩阵链可以被看作较小尺寸的子问题。因此，可以使用递归方便地求解。递归的实现代码如下：

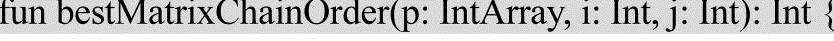
程序的运行结果如下：

最少的乘法次数为42

这种方法的时间复杂度是指数级的。可以注意到，这种算法会对一些子问题进行重复的计算。例如在计算（A）（BCD）这种方案的时候会计算C*D的代价，而在计算（AB）（CD）这种方案的时候又会重复计算C*D的代价。显然子问题是有重叠的，对此，通常可以用动态规划的方法来降低时间复杂度。

方法二：动态规划

典型的动态规划的方法是使用自下而上的方式来构造临时数组以保存子问题的中间结果，从而可以避免大量重复的计算。实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（n^3），空间复杂度为O（n^2）。

4.21 如何求解迷宫问题

【出自YMX笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个大小为N×N的迷宫，一只老鼠需要从迷宫的左上角（对应矩阵的[0][0]）走到迷宫的右下角（对应矩阵的[N-1][N-1]），老鼠只能向两个方向移动：向右或向下。在迷宫中，0表示没有路（是死胡同），1表示有路。例如：给定下面的迷宫：

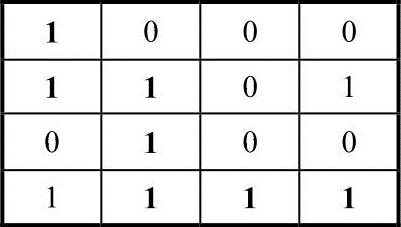
图中标粗的路径就是一条合理的路径。请给出算法来找到这样一条合理路径。

分析与解答：

最容易想到的方法就是尝试所有可能的路径，找出可达的一条路。显然这种方法效率非常低，这里重点介绍一种效率更高的回溯法。主要思路为：当碰到死胡同的时候，回溯到前一步，然后从前一步出发继续寻找可达的路径。算法的主要框架如下：

申请一个结果矩阵来标记移动的路径

if到达了目的地

打印解决方案矩阵

else

（1）在结果矩阵中标记当前为1（1表示移动的路径）。

（2）向右前进一步，然后递归地检查，走完这一步后，判断是否存在到终点的可达的路线。

（3）如果步骤（2）中的移动方法导致没有通往终点的路径，那么选择向下移动一步，然后检查使用这种移动方法后，是否存在到终点的可达的路线。

（4）如果上面的移动方法都会导致没有可达的路径，那么标记当前单元格在结果矩阵中为0，返回false，并回溯到前一步中。根据以上框架很容易进行代码实现。示例代码如下：

程序的运行结果如下：

1 0 0 0

1 1 0 0

0 1 0 0

0 1 1 1

4.22 如何从三个有序数组中找出它们的公共元素

【出自YMX笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定以非递减顺序排序的三个数组，找出这三个数组中的所有公共元素。例如，给出下面三个数组：ar1[]={2，5，12，20，45，85}，ar2[]={16，19，20，85，200}，ar3[]={3，4，15，20，39，72，85，190}。那么这三个数组的公共元素为{20，85}。

分析与解答：

最容易想到的方法是首先找出两个数组的交集，然后再把这个交集存储在一个临时数组中，最后再找出这个临时数组与第三个数组的交集。这种方法的时间复杂度为O（N1+N2+N3），其中N1、N2和N3分别为三个数组的大小。这种方法不仅需要额外的存储空间，而且还需要额外的两次循环遍历。下面介绍另外一种只需要一次循环遍历、而且不需要额外存储空间的方法，主要思路如下：

假设当前遍历的三个数组的元素分别为ar1[i]、ar2[j]和ar3[k]，则存在以下几种可能性：

（1）如果ar1[i]、ar2[j]和ar3[k]相等，则说明当前遍历的元素是三个数组的公有元素，可以直接打印出来，然后通过执行i++，j++，k++，使三个数组同时向后移动，此时继续遍历各数组后面的元素。

（2）如果ar1[i]＜ar2[j]，则执行i++来继续遍历ar1中后面的元素，因为ar1[i]不可能是三个数组公有的元素。

（3）如果ar2[j]＜ar3[k]，同理可以通过j++来继续遍历ar2后面的元素。

（4）如果前面的条件都不满足，说明ar1[i]＞ar2[j]而且ar2[j]＞ar3[k]，此时可以通过k++来继续遍历ar3后面的元素。

实现代码如下：

程序的运行结果如下：

20 85

算法性能分析：

这种方法的时间复杂度为O（N1+N2+N3）。

4.23 如何求两个有序集合的交集

【出自WY笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

有两个有序的集合，集合中的每个元素都是一段范围，求其交集，例如集合{[4，8]，[9，13]}和{[6，12]}的交集为{[6，8]，[9，12]}。

分析与解答：

方法一：蛮力法

最简单的方法就是遍历两个集合，针对集合中的每个元素判断是否有交集，如果有，则求出它们的交集，实现代码如下：

代码运行结果如下：

[6，8]

[9，12]

算法性能分析：

这种方法的时间复杂度为O（n^2）。

方法二：特征法

上述这种方法显然没有用到集合有序的特点，因此，它不是最佳的方法。假设两个集合为s1和s2。当前比较的集合为s1[i]和s2[j]，其中，i与j分别表示的是集合s1与s2的下标。可以分为如下几种情况：

1）s1集合的下界小于s2的上界：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]显然没有交集，那么接下来只有s1[i+1]与s2[j]才有可能会有交集。

2）s1的上界介于s2的下界与上界之间：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]有交集（s2[j]的下界和s1[i]的上界），那么接下来只有s1[i+1]与s2[j]才有可能会有交集。

3）s1包含s2：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]有交集（交集为s2[j]），那么接下来只有s1[i]与s2[j+1]才有可能会有交集。

4）s2包含s1：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]有交集（交集为s1[i]），那么接下来只有s1[i+1]与s2[j]才有可能会有交集。

5）s1的下界介于s2的下界与上界之间：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]有交集（交集为s1[i]的下界和s2[j]的上界），那么接下来只有s1[i]与s2[j+1]才有可能会有交集。

6）s2的上界小于s1的下界：

S1[i] ____

S2[j] ____

在这种情况下，s1[i]和s2[j]显然没有交集，那么接下来只有s1[i]与s2[j+1]才有可能会有交集。

根据以上分析给出实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（n1+n2），其中n1、n2分别为两个集合的大小。

4.24 如何对有大量重复数字的数组排序

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个数组，已知这个数组中有大量的重复的数字，如何对这个数组进行高效地排序？

分析与解答：

如果使用常规的排序方法，虽然最好的排序算法的时间复杂度为O（NlogN），但是使用常规排序算法显然没有用到数组中有大量重复数字这个特性。如何能使用这个特性呢？下面介绍两种更加高效的算法。

方法一：AVL树

这种方法的主要思路是：根据数组中的数构建一个AVL树，这里需要对AVL树做适当的扩展，在结点中增加一个额外的数据域来记录这个数字出现的次数，在AVL树构建完成后，可以对AVL树进行中序遍历，根据每个结点对应数字出现的次数，把遍历结果放回到数组中就完成了排序，实现代码如下：

代码运行结果如下：

2 2 2 3 3 3 12 12 12 15 15 100

算法性能分析：

这种方法的时间复杂度为O（NLogM），其中，N为数组的大小，M为数组中不同数字的个数，空间复杂度为O（N）。

方法二：哈希法

这种方法的主要思路为创建一个哈希表，然后遍历数组，把数组中的数字放入哈希表中，在遍历的过程中，如果这个数在哈希表中存在，则直接把哈希表中这个key对应的value加1；如果这个数在哈希表中不存在，则直接把这个数添加到哈希表中，并且初始化这个key对应的value为1。实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（N+MLogM），空间复杂度为O（M）。

4.25 如何对任务进行调度

【出自MT面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

假设有一个中央调度机，有n个相同的任务需要调度到m台服务器上去执行，由于每台服务器的配置不一样，因此，服务器执行一个任务所花费的时间也不同。现在假设第i个服务器执行一个任务需要的时间为t[i]。例如：有2个执行机a与b，执行一个任务分别需要7min和10min，有6个任务待调度。如果平分这6个任务，即a与b各3个任务，则最短需要30min执行完所有。如果a分4个任务，b分2个任务，则最短28min执行完。请设计调度算法，使得所有任务完成所需要的时间最短。输入m台服务器，每台机器处理一个任务的时间为t[i]，完成n个任务，输出n个任务在m台服务器的分布。intestimate_process_time（int[]t，intm，intn）。

分析与解答：

本题可以采用贪心法来解决，具体实现思路如下：

申请一个数组来记录每台机器的执行时间，初始化为0，在调度任务的时候，对于每个任务，在选取机器的时候采用如下的贪心策略：对于每台机器，计算机器已经分配任务的执行时间+这个任务需要的时间，选用最短时间的机器进行处理。实现代码如下：

程序的运行结果如下：

第1台服务器有4个任务，执行总时间为：28

第2台服务器有2个任务，执行总时间为：20

执行完所有任务所需的时间为28

算法性能分析：

这种方法使用了双重循环，因此，时间复杂度为O（mn）。

4.26 如何对磁盘分区

【出自XM面题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

有N个磁盘，每个磁盘大小为D[i]（i=0…N-1），现在要在这N个磁盘上“顺序分配”M个分区，每个分区大小为P[j]（j=0…M-1），顺序分配的意思是：分配一个分区P[j]时，如果当前磁盘剩余空间足够，则在当前磁盘分配；如果不够，则尝试下一个磁盘，直到找到一个磁盘D[i+k]可以容纳该分区，分配下一个分区P[j+1]时，则从当前磁盘D[i+k]的剩余空间开始分配，不再使用D[i+k]之前磁盘末分配的空间，如果这M个分区不能在这N个磁盘完全分配，则认为分配失败，请实现函数，is_allocable判断给定N个磁盘（数组D）和M个分区（数组P），是否会出现分配失败的情况？举例：磁盘为[120，120，120]，分区为[60，60，80，20，80]可分配，如果为[60，80，80，20，80]，则分配失败。

分析与解答：

本题的主要思路如下：对所有的分区进行遍历，同时用一个变量dIndex记录上次分配磁盘的下标，初始化为0；对于每个分区，从上次分配的磁盘开始继续分配，如果没有足够的空间，则顺序找其他的磁盘，直到找到合适的磁盘为止，进行分配；如果找不到合适的磁盘，则分配失败，实现代码如下：

程序的运行结果如下：

分配成功

算法性能分析：

这种方法使用了双重循环，因此，时间复杂度为O（MN）。

第5章 字符串

字符串是由数字、字母和下划线组成的一串字符，是最常用的数据结构之一，几乎所有的程序员面试笔试中没有不考字符串的。相对而言，由于字符串是一种较为简单的数据结构，凡是有一点编程基础的人都会对此比较熟悉，所以自然而然它也容易引起面试官的反复发问。其实，通过考察字符串的一些细节，能够看出求职者的编程习惯，进而反映出求职者在操作系统、软件工程以及边界内存处理等方面的知识掌握能力，而这些能力往往也是企业是否录用求职者的重要参考因素。

5.1 如何求一个字符串的所有排列

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

实现一个方法，当输入一个字符串时，要求输出这个字符串的所有排列。例如输入字符串abc，要求输出由字符a、b、c所能排列出来的所有字符串：abc、acb、bac、bca、cab及cba。

分析与解答：

这道题主要考察对递归的理解，可以采用递归的方法来实现。当然也可以使用非递归的方法来实现，但是与递归法相比，非递归法难度增加了很多。下面分别介绍这两种方法。

方法一：递归法

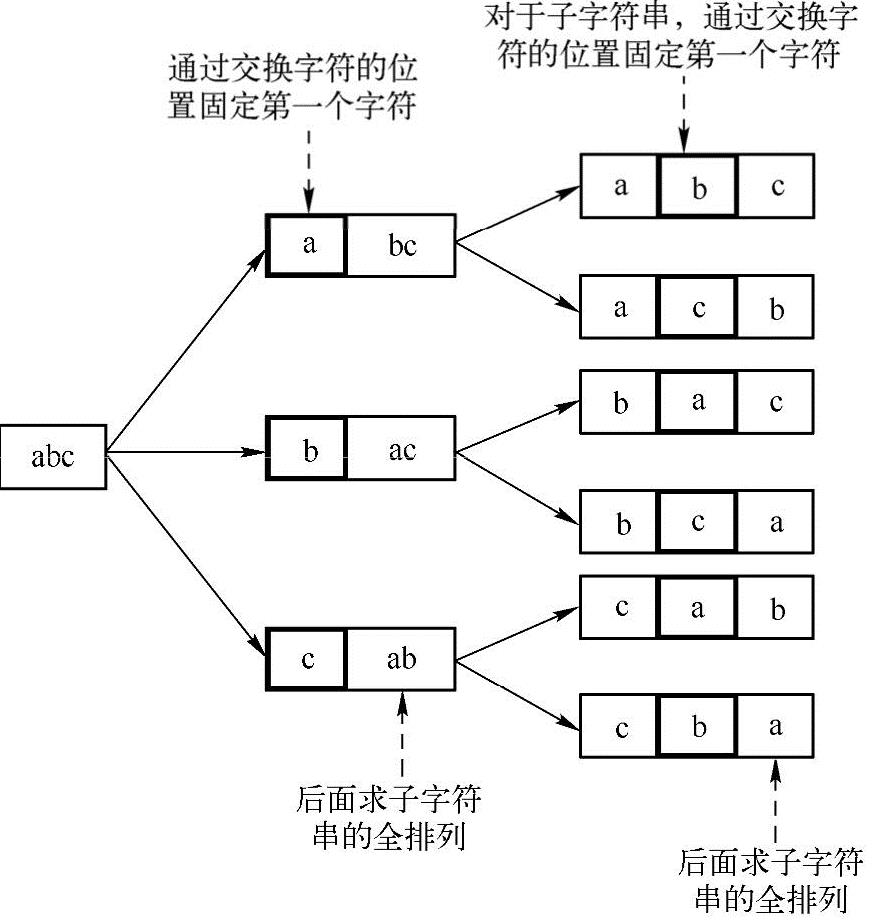
下面以字符串abc为例介绍对字符串进行全排列的方法。具体步骤如下：

（1）首先固定第一个字符a，然后对后面的两个字符b与c进行全排列。

（2）交换第一个字符与其后面的字符，即交换a与b，然后固定第一个字符b，接着对后面的两个字符a与c进行全排列。

（3）由于第（2）步交换了a和b破坏了字符串原来的顺序，因此，需要再次交换a和b使其恢复到原来的顺序，然后交换第一个字符与第三个字符（交换a和c），接着固定第一个字符c，对后面的两个字符a与b求全排列。

在对字符串求全排列的时候就可以采用递归的方式来求解，实现方法如下图所示：

在使用递归方法求解的时候，需要注意以下两个问题：（1）逐渐缩小问题的规模，并且可以用同样的方法来求解子问题。（2）递归一定要有结束条件，否则会导致程序陷入死循环。本题目递归方法实现代码如下：

程序的运行结果如下：

abc acb bac bca cba cab

算法性能分析：

假设这种方法需要的基本操作数为f（n），那么f（n）=n*f（n-1）=n*（n-1）*f（n-2）…=n！。所以，算法的时间复杂度为O（n！）。算法在对字符进行交换的时候用到了常量个指针变量，因此，算法的空间复杂度为O（1）。

方法二：非递归法

递归法比较符合人的思维，因此，算法的思路以及算法实现都比较容易。下面介绍另外一种非递归的方法。算法的主要思想是：从当前字符串出发找出下一个排列（下一个排列为大于当前字符串的最小字符串）。

通过引入一个例子来介绍非递归算法的基本思想：假设要对字符串“12345”进行排序。第一个排列一定是“12345”，依此获取下一个排列：“12345”-＞“12354”-＞“12435”-＞“12453”-＞“12534”-＞“12543”-＞“13245”-＞…。从“12543”-＞“13245”可以看出找下一个排列的主要思路是：（1）从右到左找到两个相邻递增（从左向右看是递增的）的字符串，例如“12543”，从右到左找出第一个相邻递增的子串为“25”；记录这个小的字符的下标为pmin。（2）找出pmin后面的比它大的最小的字符进行交换，在本例中‘2’后面的子串中比它大的最小的字符为‘3’，因此，交换‘2’和‘3’得到字符串“13542”。（3）为了保证下一个排列为大于当前字符串的最小字符串，在第（2）步中完成交换后需要对pmin后的子串重新组合，使其值最小，只需对pmin后面的字符进行逆序即可（因为此时pmin后面的子字符串中的字符必定是按照降序排列，逆序后字符就按照升序排列了），逆序后就能保证当前的组合是新的最小的字符串。在这个例子中，上一步得到的字符串为“13542”，pmin指向字符‘3’，对其后面的子串“542”逆序后得到字符串“13245”。（4）当找不到相邻递增的子串时，说明找到了所有的组合。

需要注意的是，这种方法适用于字符串中的字符是按照升序排列的情况。因此，非递归方法的主要思路是：（1）首先对字符串进行排序（按字符进行升序排列）。（2）依次获取当前字符串的下一个组合直到找不到相邻递增的子串为止。实现代码如下：

程序的运行结果如下：

abc acb bac bca cab cba

算法性能分析：

首先对字符串进行排序的时间复杂度为O（n^2），接着求字符串的全排列，由于长度为n的字符串全排列个数为n！，因此Permutation函数中的循环执行的次数为n！，循环内部调用函数getNextPermutation，getNextPermutation内部用到了双重循环，因此它的时间复杂度为O（n^2）。所以，求全排列算法的时间复杂度为O（n！*n^2）。

引申：如何去掉重复的排列

分析与解答：

当字符串中没有重复的字符的时候，它的所有组合对应的字符串也就没有重复的情况，但是当字符串中有重复的字符的时候，例如“baa”，此时如果按照上面介绍的算法求全排列的时候就会有重复的字符串。

由于全排列的主要思路是：从第一个字符起每个字符分别与它后面的字符进行交换：例如：对于“baa”，交换第一个与第二个字符后得到“aba”，再考虑交换第一个与第三个字符后得到“aab”，由于第二个字符与第三个字符相等，因此，会导致这两种交换方式对应的全排列是重复的（在固定第一个字符的情况下它们对应的全排列都为“aab”和“aba”）。从上面的分析可以看出去掉重复排列的主要思路是：从第一个字符起每个字符分别与它后面非重复出现的字符进行交换。在递归方法的基础上只需要增加一个判断字符是否重复的函数即可，实现代码如下：

程序的运行结果如下：

aba aab baa

5.2 如何求两个字符串的最长公共子串

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

找出两个字符串的最长公共子串，例如字符串“abccade”与字符串“dgcadde”的最长公共子串为“cad”。

分析与解答：

对于这道题而言，最容易想到的方法就是采用蛮力法，假设字符串s1与s2的长度分别为len1和len2（假设len1≥len2），首先可以找出s2的所有可能的子串，然后判断这些子串是否也是s1的子串，通过这种方法可以非常容易地找出两个字符串的最长子串。当然，这种方法的效率是非常低的，主要原因是：s2中的大部分字符需要与s1进行很多次的比较。那么是否有更好的方法来减少比较的次数呢？下面介绍两种通过减少比较次数从而降低时间复杂度的方法。

方法一：动态规划法

通过把中间的比较结果记录下来，从而可以避免字符的重复比较。主要思路如下：

首先定义二元函数f（i，j）：表示分别以s1[i]，s2[j]结尾的公共子串的长度，显然，f（0，j）=0（j＞=0），f（i，0）=0（i＞=0），那么，对于f（i+1，j+1）而言，则有如下两种取值：

（1）f（i+1，j+1）=0，当str1[i+1]！=str2[j+1]时；

（2）f（i+1，j+1）=f（i，j）+1，当str1[i+1]==str2[j+1]时；

根据这个公式可以计算出f（i，j）（0=＜i＜=len（s1），0=＜j＜=len（s2））所有的值，从而可以找出最长的子串，如下图所示：

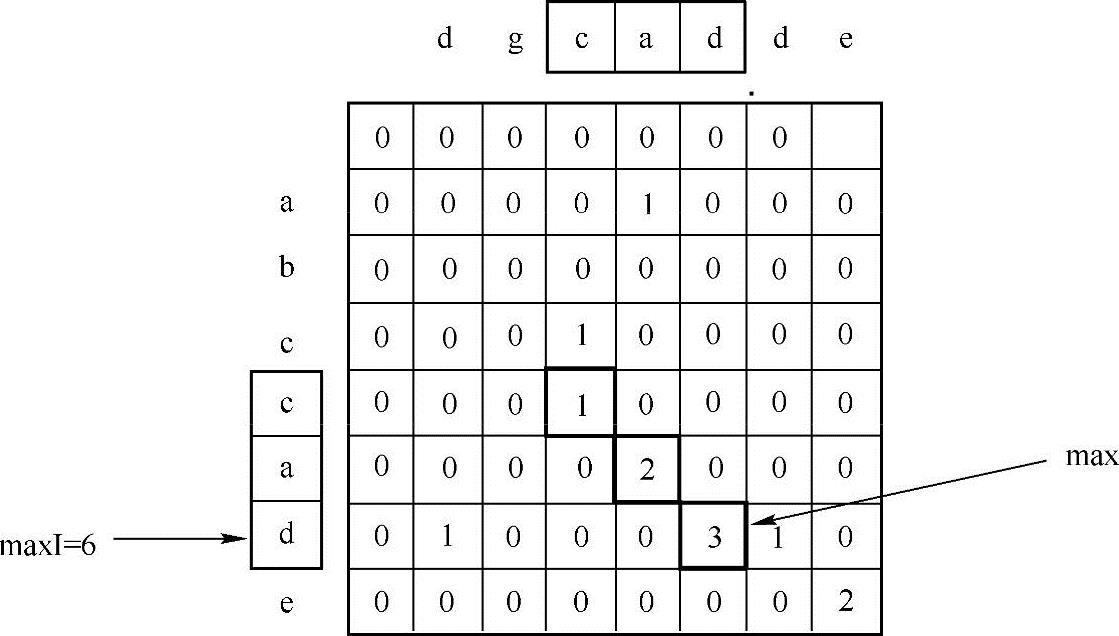
通过上图所示的计算结果，可以求出最长公共子串的长度max与最长子串结尾字符在字符数组中的位置maxI，由这两个值就可以唯一确定一个最长公共子串为“cad”，这个子串在数组中的起始下标为：maxI-max=3，子串长度为max=3。实现代码如下：

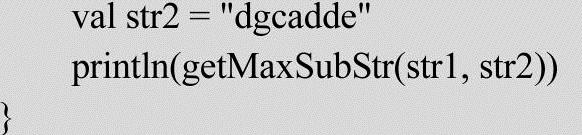
程序的运行结果如下：

cad

算法性能分析：

由于这种方法使用了二重循环分别遍历两个字符数组，因此，时间复杂度为O（m*n）（其中，m和n分别为两个字符串的长度），此外，由于这种方法申请了一个m*n的二维数组，因此，算法的空间复杂度也为O（m*n）。很显然，这种方法的主要缺点为申请了m*n个额外的存储空间。

方法二：滑动比较法

如下图所示，这种方法的主要思路是：保持s1的位置不变，然后移动s2，接着比较它们重叠的字符串的公共子串（记录最大的公共子串的长度maxLen，以及最长公共子串在s1中结束的位置maxLenEnd1），在移动的过程中，如果当前重叠子串的长度大于maxLen，则更新maxLen为当前重叠子串的长度。最后通过maxLen和maxLenEnd1就可以找出它们最长的公共子串。实现方法如下图所示：

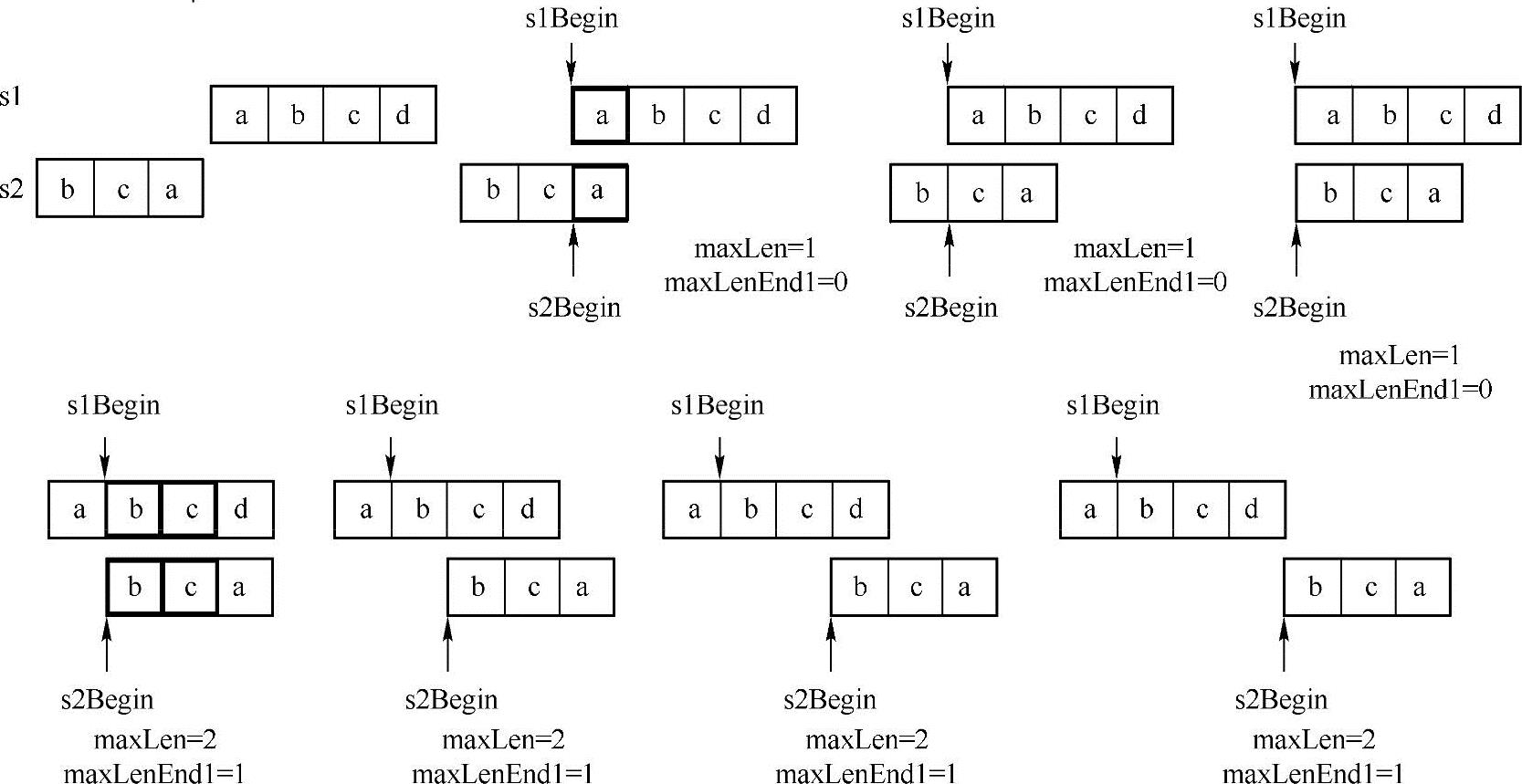
如上图所示，这两个字符串的最长公共子串为"bc"，实现代码如下：

算法性能分析：

这种方法用双重循环来实现，外层循环的次数为m+n（其中，m和n分别为两个字符串的长度），内层循环最多执行n次，算法的时间复杂度为O（（m+n）*n）。此外，这种方法只使用了几个临时变量，因此算法的空间复杂度为O（1）。

5.3 如何对字符串进行反转

【出自WR面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

实现字符串的反转，要求不使用任何系统方法，且时间复杂度最小。

分析与解答：

字符串的反转主要通过字符的交换来实现，需要首先把字符串转换为字符数组，然后定义两个索引分别指向数组的首尾，再交换两个索引位置的值，同时把两个索引的值向中间移动，直到两个索引相遇为止，则完成了字符串的反转。根据字符交换方法的不同，可以采用如下两种实现方法。

方法一：临时变量法

最常用的交换两个变量的方法为定义一个中间变量来交换两个值，主要思路是：假如要交换a与b，通过定义一个中间变量temp来实现变量的交换：temp=a；a=b；b=a。实现代码如下：

程序的运行结果如下：

字符串abcdefg翻转后为：gfedcba

算法性能分析：

这种方法只需要对字符数组变量遍历一次，因此时间复杂度为O（N）（N为字符串的长度）。

方法二：直接交换法

在交换两个变量的时候，另外一种常用的方法为异或的方法，这种方法主要基于如下的特性：a^a=0、a^0=a以及异或操作满足交换律与结合律。假设要交换两个变量a与b，则可以采用如下方法实现：

a=a^b；

b=a^b； //b=a^b=（a^b）^b=a^（b^b）=a^0=a

a=a^b； //a=a^b=（a^b）^a=（b^a）^a=b^（a^a）=b^0=b

实现代码如下：

算法性能分析：

这种方法只需要对字符数组遍历一次，因此时间复杂度为O（N）（N为字符串的长度），与方法一相比，这种方法在实现字符交换的时候不需要额外的变量。

引申：如何实现单词反转

题目描述：把一个句子中的单词进行反转，例如：“howareyou”，进行反转后为“youarehow”。

分析与解答：

主要思路：对字符串进行两次反转操作，第一次对整个字符串中的字符进行反转，反转结果为：“uoyerawoh”，通过这一次的反转已经实现了单词顺序的反转，只不过每个单词中字符的顺序反了，接下来只需要对每个单词进行字符反转即可得到想要的结果：“youare how”。实现代码如下：

程序的运行结果如下：

字符串how are you翻转后为：you are how

算法性能分析：

这种方法对字符串进行了两次遍历，因此时间复杂度为O（N）。

5.4 如何判断两个字符串是否为换位字符串

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

换位字符串是指组成字符串的字符相同，但位置不同。例如：由于字符串“aaaabbc”与字符串“abcbaaa”就是由相同的字符所组成的，因此它们是换位字符。

分析与解答：

在算法设计中，经常会采用空间换时间的方法以降低时间复杂度，即通过增加额外的存储空间来达到优化算法性能的目的。就本题而言，假设字符串中只使用ASCII字符，由于ASCII字符共有266个（对应的编码为0～255），在实现的时候可以通过申请大小为266的数组来记录各个字符出现的个数，并将其初始化为0，然后遍历第一个字符串，将字符对应的ASCII码值作为数组下标，把对应数组的元素加1，然后遍历第二个字符串，把数组中对应的元素值-1。如果最后数组中各个元素的值都为0，说明这两个字符串是由相同的字符所组成的；否则，这两个字符串是由不同的字符所组成的。实现代码如下。

程序的运行结果如下：

aaaabbc和abcbaaa是换位字符

算法性能分析：

这种方法的时间复杂度为O（N）。

5.5 如何判断两个字符串的包含关系

【出自GG面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定由字母组成的字符串s1和s2，其中，s2中字母的个数少于s1，如何判断s1是否包含s2？即出现在s2中的字符在s1中都存在。例如s1=“abcdef”，s2=“acf”，那么s1就包含s2；如果s1=“abcdef”，s2=“acg”，那么s1就不包含s2，因为s2中有“g”，但是s1中没有“g”。

分析与解答：

方法一：直接法

最直接的方法就是对于s2中的每个字符，通过遍历字符串s1查看是否包含该字符。实现代码如下：

程序的运行结果如下：

abcdef与acf有包含关系

算法性能分析：

这种方法的时间复杂度为O（m*n），其中，m与n分别表示两个字符串的长度。

方法二：空间换时间法

首先，定义一个flag数组来记录较短的字符串中字符出现的情况，如果出现，则标记为1，否则标记为0，同时记录flag数组中1的个数count；接着遍历较长的字符串，对于字符a，若原来flag[a]==1，则修改flag[a]=0，并将count减1；若flag[a]==0，则不做处理。最后判断count的值，如果count==0，则说明这两个字符有包含关系。实现代码如下：

算法性能分析：

这种方法只需要对两个数组分别遍历一遍，因此，时间复杂度为O（m+n）（其中m，n分别为两个字符串的长度），与方法一和方法二相比，本方法的效率有了明显的提升，但是其缺点是申请了52个额外的存储空间。

5.6 如何对由大小写字母组成的字符数组排序

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

有一个由大小写字母组成的字符串，请对它进行重新组合，使得其中的所有小写字母排在大写字母的前面（大写或小写字母之间不要求保持原来次序）。

分析与解答：

本题目可以使用类似快速排序的方法处理，可以用两个索引分别指向字符串的首和尾，首索引正向遍历字符串，找到第一个大写字母，尾索引逆向遍历字符串，找到第一个小写字母，交换两个索引位置的字符，然后将两个索引沿着相应的方向继续向前移动，重复上述步骤，直到首索引大于或等于尾索引为止。具体实现如下：

程序的运行结果如下：

fbceDA

算法性能分析：

这种方法对字符串只进行了一次遍历，因此，算法的时间复杂度为O（N），其中，N是字符串的长度。

5.7 如何消除字符串的内嵌括号

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个如下格式的字符串：（1，（2，3），（4，（5，6），7）），括号内的元素可以是数字，也可以是另一个括号，实现一个算法消除嵌套的括号，例如把上面的表达式变成（1，2，3，4，5，6，7），如果表达式有误，则报错。

分析与解答：

从问题描述可以看出，这道题要求实现两个功能：一个是判断表达式是否正确，另一个是消除表达式中嵌套的括号。对于判定表达式是否正确这个问题，可以从如下几个方面来入手：首先，表达式中只有数字、逗号和括号这几种字符，如果有其他的字符出现，则是非法表达式；其次，判断括号是否匹配，如果碰到‘（’，则把括号的计数器的值加上1；如果碰到‘）’，那么判断此时计数器的值，如果计数器的值大于1，则把计数器的值减去1，否则为非法表达式，当遍历完表达式后，括号计数器的值为0，则说明括号是配对出现的，否则括号不配对，表达式为非法表达式。对于消除括号这个问题，可以通过申请一个额外的存储空间，在遍历原字符串的时候把除了括号以外的字符保存到新申请的额外的存储空间中，这样就可以去掉嵌套的括号了。需要特别注意的是，字符串首尾的括号还需要保存。实现代码如下：

程序的运行结果如下：

（1，（2，3），（4，（5，6），7））去除嵌套括号后为：（1，2，3，4，5，6，7）

算法性能分析：

这种方法对字符串进行了一次遍历，因此时间复杂度为O（N）（其中，N为字符串的长度）。此外，这种方法申请了额外的N+1个存储空间，因此空间复杂度也为O（N）。

5.8 如何判断字符串是否是整数

【出自HW笔试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述

写一个方法，检查字符串是否是整数，如果是，则返回其整数值。

分析与解答：

整数分为负数与非负数，负数只有一种表示方法，而整数可以有两种表示方法。例如：-123，123，+123。因此在判断字符串是否为整数的时候，需要把这几个问题都考虑到。下面主要介绍两种方法。

方法一：递归法

对于整数而言，例如123，可以看成12*10+3，而12又可以看成1*10+2。而-123可以看成（-12）*10-3，-12可以被看成（-1）*10-2。根据这个特点，可以采用递归的方法来求解，可以首先根据字符串的第一个字符确定整数的正负，接着对字符串从右往左遍历，假设字符串为“c₁c₂c₃c_n”，如果cn不是整数，那么这个字符串不能表示成整数；如果这个数是非负数（c1！=‘-’），那么这个整数的值为“c₁c₂c₃…c_n-1”对应的整数值乘以10加上cn对应的整数值，如果这个数是负数（c1==‘-’），那么这个整数的值为c₁c₂c₃…c_n-1对应的整数值乘以10减去cn对应的整数值。而求解子字符串“c1c2c3…sc-1”对应的整数的时候，可以用相同的方法来求解，因此可以采用递归的方法来求解。对于“+123”，可以首先去掉“+”，然后处理方法与“123”相同。由此可以得到递归表达式为

c1==‘-’？toint（“c1c2c3cn-1”）*10-（cn-'0'）：toint（“c1c2c3cn-1”）*10+（cn-'0'）。

递归的结束条件是：当字符串长度为1时，直接返回字符对应的整数的值。实现代码如下：

程序的运行结果如下：

-543

543

543

不是数字

算法性能分析：

由于这种方法对字符串进行了一次遍历，因此时间复杂度为O（N）（其中，N是字符串的长度）。

方法二：非递归法

首先通过第一个字符的值确定整数的正负性，然后去掉符号位，把后面的字符串当作正数来处理，处理完成后再根据正负性返回正确的结果。实现方法为从左到右遍历字符串计算整数的值，以“123”为例，遍历到‘1’的时候结果为1，遍历到‘2’的时候结果为1*10+2=12，遍历到‘3’的时候结果为12*10+3=123。其本质思路与方法一类似，根据这个思路实现代码如下：

算法性能分析：

由于这种方法对字符串进行了一次遍历，因此，算法的时间复杂度为O（N）（其中，N是指字符串的长度）。但是由于方法一采用了递归法，而递归法需要大量的函数调用，也就有大量的压栈与弹栈操作（函数调用都是通过压栈与弹栈操作来完成的）。因此，虽然这两个方法有相同的时间复杂度，但是方法二的运行速度会比方法一更快，效率更高。

5.9 如何实现字符串的匹配

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定主字符串s与模式字符串P，判断P是否是S的子串，如果是，则找出P在S中第一次出现的下标。

分析与解答：

对于字符串的匹配，最直接的方法就是挨个比较字符串中的字符，这种方法比较容易实现，但是效率也比较低。对于这种字符串匹配的问题，除了最常见的直接比较法外，经典的KMP算法也是不二选择，它能够显著提高运行效率，下面分别介绍这两种方法。

方法一：直接计算法

假定主串S=“S₀S₁S₂…S_m”，模式串P=“P₀P₁P₂P_n”。实现方法是：比较从主串S中以S_i（0＜=i＜m）为首的字符串和模式串P，判断P是否为S的前缀，如果是，那么P在S中第一次出现的位置则为i，否则接着比较从S_i+1开始的子串与模式串P，这种方法的时间复杂度为O（m*n）。此外如果i＞m-n的时候，在主串中以S_i为首的子串的长度必定小于模式串P的长度，因此，在这种情况下就没有必要再做比较了。实现代码如下：

程序的运行结果如下：

3

算法性能分析：

这种方法在最差的情况下需要对模式串P遍历m-n次（m、n分别为主串和模式串的长度），因此，算法的时间复杂度为O（n（m-n））。

方法二：KMP算法

在方法一中，如果“P₀P₁P₂…P_j-1”==“S_i-j…Si_-1”，模式串的前j个字符已经和主串中i-j到i-1的字符进行了比较，此时如果P_j！=S_i，那么模式串需要回退到0，主串需要回退到i-j+1的位置重新开始下一次比较。而在KMP算法中，如果P_j！=S_i，那么不需要回退，即i保持不动，j也不用清零，而是向右滑动模式串，用P_k和S_i继续匹配。这种方法的核心就是确定k的大小，显然，k的值越大越好。

如果P_j！=S_i，可以继续用P_k和S_i进行比较，那么必须满足：

（1）“P₀P₁P₂…P_k-1”==“S_i-kS_i-1”

已经匹配的结果应满足下面的关系：

（2）“P_j-k…P_j-1”==“S_i-k…S_i-1”

由以上这两个公式可以得出如下结论：

“P₀P₁P₂…P_k-1”=“P_j-k…P_j-1”

因此，当模式串满足“P₀P₁P₂…P_k-1”==“P_j-k…P_j-1”时，如果主串第i个字符与模式串第j个字符匹配失败，只需要接着比较主串第i个字符与模式串第k个字符。

为了在任何字符匹配失败的时候都能找到对应k的值，这里给出next数组的定义，next[i]=m表示的意思为“p₀p₁p_m-1”=“p_i-m…p_i-2p_i-1”。计算方法如下：

（1）next[j]=-1（当j==0时）。

（2）next[j]=max（Max{k|1＜k＜j且“p₀…p_k”==“p_j-k-1…p_j-1”}）

（3）next[j]=0（其他情况）

实现代码如下：

程序的运行结果如下：

从运行结果可以看出，模式串P="abaabc"的next数组为{-1，0，0，1，1}，next[3]=1，说明P[0]==P[2]。当i=3、j=3的时候S[i]！=P[j]，此时主串S不需要回溯，跟模式串位置j=next[j]=next[3]=1的字符继续进行比较。因为此时S[i-1]一定与P[0]相等，所以就没有必要再比较了。

算法性能分析：

这种方法在求next数组的时候循环执行的次数为n（n为模式串的长度），在模式串与主串匹配的过程中循环执行的次数为m（m为主串的长度）。因此，算法的时间复杂度为O（m+n）。但是由于算法申请了额外的n个存储空间来存储next数组，因此，算法的空间复杂度为O（n）。

5.10 如何求字符串里的最长回文子串

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

回文字符串是指一个字符串从左到右与从右到左遍历得到的序列是相同的。例如“abcba”就是回文字符串，而“abcab”则不是回文字符串。

分析与解答：

最容易想到的方法为遍历字符串所有可能的子串（蛮力法），判断其是否为回文字符串，然后找出最长的回文子串。但是当字符串很长的时候，这种方法的效率是非常低的，因此这种方法不可取。下面介绍几种相对高效的方法。

方法一：动态规划法

在采用蛮力法找回文子串的时候有很多字符的比较是重复的，因此，可以把前面比较的中间结果记录下来供后面使用。这就是动态规划的基本思想。那么如何根据前面查找的结果，判断后续的子串是否为回文字符串呢？下面给出判断的公式，即动态规划的状态转移公式。

给定字符串“S₀S₁S₂…S_n”，假设P（i，j）=1表示“S_iS_i+1…S_j”是回文字符串；P（i，j）=0则表示“S_iS_i+1…S_j”不是回文字符串。那么：

P（i，i）=1

如果Si==Si+1，则P（i，i+1）=1，否则P（i，i+1）=0。

如果Si+1==Sj+1，则P（i+1，j+1）=P（i，j）。

根据这几个公式，实现代码如下：

程序的运行结果如下：

最长的回文子串为：defgfed

算法性能分析：

这种方法的时间复杂度为O（n^2），空间复杂度也为O（n^2）。

此外，还有另外一种动态规划的方法来实现最长回文字符串的查找。主要思路是：对于给定的字符串str1，求出对其进行逆序的字符串str2，然后str1与str2的最长公共子串就是str1的最长回文子串。

方法二：中心扩展法

判断一个字符串是否为回文字符串最简单的方法是：从字符串最中间的字符开始向两边扩展，通过比较左右两边字符是否相等就可以确定这个字符串是否为回文字符串。这种方法对于字符串长度为奇数和偶数的情况需要分别对待。例如：对于字符串“aba”，就可以从最中间的位置b开始向两边扩展；但是对于字符串“baab”，就需要从中间的两个字母开始分别向左右两边扩展。

基于回文字符串的这个特点，可以设计这样一个方法来找回文字符串：对于字符串中的每个字符C_i，向两边扩展，找出以这个字符为中心的回文子串的长度。由于上面介绍的回文字符串长度的奇偶性，这里需要分两种情况：（1）以C_i为中心向两边扩展；（2）以C_i和C_i+1为中心向两边扩展。实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（n^2），空间复杂度为O（1）。

方法三：Manacher算法

方法二需要根据字符串的长度分偶数与奇数两种不同情况单独处理，Manacher算法可以通过向相邻字符中插入一个分隔符，把回文字符串的长度都变为奇数，从而可以对这两种情况统一处理。例如：对字符串“aba”插入分隔符后变为“*a*b*a*”，回文字符串的长度还是奇数。对字符串“aa”插入分隔符后变为“*a*a*”，回文字符串长度也是奇数。因此，采用这种方法后可以对这两种情况统一进行处理。

Manacher算法的主要思路是：首先在字符串中相邻的字符中插入分割字符，字符串的首尾也插入分割字符（字符串中不存在的字符，本例以字符*为例作为分割字符）。接着用另外的一个辅助数组P来记录以每个字符为中心对应的回文字符串的信息。P[i]记录了以字符串第i个字符为中心的回文字符串的半径（包含这个字符），以P[i]为中心的回文字符串的长度为2*P[i]-1。P[i]-1就是这个回文字符串在原来字符串中的长度。例如：“*a*b*a*”对应的辅助数组P为{1，2，1，4，1，2，1}，最大值为P[3]=4，那么原回文字符串的长度则为4-1=3。

那么如何来计算P[i]的值呢，如下图所示可以分为四种情况来讨论：

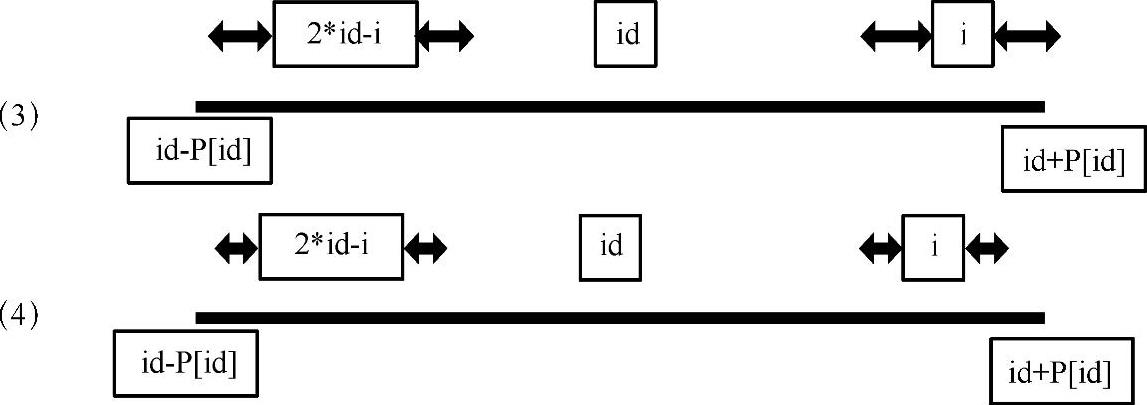
假设在计算P[i]的时候，在已经求出的P[id]（id＜i）中，找出使得id+p[id]的值为最大的id，即找出这些回文字符串的尾字符下标最大的回文字符的中心的下标id。

（1）i没有落到P[id]对应的回文字符串中（如上图（1））。此时因为没有参考的值，所以只能把字符串第i个字符作为中心，向两边扩展来求P[i]的值。

（2）i落到了P[id]对应的回文字符串中。此时可以把id当作对称点，找出i对称的位置2*id-i，如果P[2*id-i]对应的回文字符的左半部分有一部分落在P[id]内，另外一部分落在P[id]外（如上图（2）），那么P[i]=id+P[id]-i，也就是P[i]的值等于P[id]与P[2*id-i]重叠部分的长度。需要注意的是，P[i]不可能比id+P[id]-i更大，证明过程如下：假设P[i]＞id+P[id]-i，以i为中心的回文字符串可以延长a、b两部分（延长的长度足够小，使得P[i]＜P[2*id-i]），如上图（2）所示：根据回文字符串的特性可以得出：a=b，找出a与b以id为对称点的子串d和c。由于d和c落在了P[2*id-i]内，因此，c=d，又因为b和c落在了P[id]内，因此，b=c，所以，可以得到a=d，这与已经求出的P[id]矛盾，因此，p[id]的值不可能更大。

（3）i落到了P[id]对应的回文字符串中，把id当作对称点，找出i对称的位置2*id-i，如果P[2*id-i]对应的回文字符的左半部分与P[id]对应的回文字符的左半部分完全重叠，则p[i]的最小值为P[2*id-i]，在此基础上继续向两边扩展，求出P[i]的值。

（4）i落到了P[id]对应的回文字符串中，把id当作对称点，找出i对称的位置2*id-i，如果P[2*id-i]对应的回文字符的左半部分完全落在了P[id]对应的回文字符的左半部分，则p[i]=P[2*id-i]。

根据以上四种情况可以得出结论：P[i]＞=MIN（P[2*id-i]，P[id]-i）。在计算时可以先求出P[i]=MIN（P[2*id-i]，P[id]-i），然后在此基础上向两边继续扩展寻找最长的回文子串，根据这个思路的实现代码如下：

程序的运行结果如下：

最长的回文子串为：abcba

算法性能分析：

这种方法的时间复杂度和空间复杂度都为O（N）。

5.11 如何按照给定的字母序列对字符数组排序

【出自QNEW笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

已知字母序列[d，g，e，c，f，b，o，a]，请实现一个方法，要求对输入的一组字符串input[]={“bed”，“dog”，“dear”，“eye”}按照字母顺序排序并打印。本例的输出顺序为dear，dog，eye，bed。

分析与解答：

这道题本质上还是考察对字符串排序的理解，唯一不同的是，改变了比较字符串大小的规则，因此这道题的关键是如何利用给定的规则比较两个字符串的大小，只要实现了两个字符串的比较，那么利用任何一种排序方法都可以。下面重点介绍字符串比较的方法。

本题的主要思路：为给定的字母序列建立一个可以进行大小比较的序列，在这里采用map数据结构来实现map的键为给定的字母序列，其值为从0开始依次递增的整数，对于没在字母序列中的字母，对应的值统一按-1来处理。其这样在比较字符串中的字符时，不是直接比较字符的大小，而是比较字符在map中对应的整数值的大小。以“bed”、“dog”为例，[d，g，e，c，f，b，o，a]构建的map为char_to_int[‘d’]=0，char_to_int[‘g’]=1，char_to_int[‘e’]=2，char_to_int[‘c’]=3，char_to_int[‘f’]=4，char_to_int[‘b’]=5，char_to_int[‘o’]=6，char_to_int[‘a’]=7。在比较“bed”与“dog”的时候，由于char_to_int[‘b’]=5，char_to_int[‘d’]=0，显然5＞0，因此，‘b’＞’d’，所以，“bed”＞“dog”。

下面以插入排序为例，给出实现代码：

程序的运行结果如下：

dea rdo geye bed

算法性能分析：

这种方法的时间复杂度为O（N^3）（其中N为字符串的长度）。因为insertSort函数中使用了双重遍历，而这个函数中调用了compare函数，所以这个函数内部也有一层循环。

5.12 如何判断一个字符串是否包含重复字符

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

判断一个字符串是否包含重复字符。例如：“good”就包含重复字符‘o’，而“abc”就不包含重复字符。

分析与解答：

方法一：蛮力法

最简单的方法就是把这个字符串看作一个字符数组，对该数组使用双重循环进行遍历，即对每个字符，都将其与其后面所有的字符进行比较，如果能找到相同的字符，则说明字符串包含重复的字符。

实现代码如下：

程序的运行结果如下：

GOOD中有重复字符

算法性能分析：

由于这种方法使用了双重循环对字符数组进行了遍历，因此，算法的时间复杂度为O（N^2）（其中，N是指字符串的长度）。

方法二：空间换时间

在算法中经常会采用空间换时间的方法。对于这个问题，也可以采取这种方法。其主要思路如下：由于常见的字符只有256个，假设这道题涉及的字符串中不同的字符个数最多为256个，那么可以申请一个大小为256的int类型数组来记录每个字符出现的次数，初始化都为0，把字符的编码作为数组的下标，在遍历字符数组的时候，如果这个字符出现的次数为0，那么把它置为1，如果为1，那么说明这个字符在前面已经出现过了，因此，字符串包含重复的字符。采用这种方法只需要对字符数组进行一次遍历即可，因此，时间复杂度为O（N），但是需要额外申请256个单位的空间。由于申请的数组用来记录一个字符是否出现，只需要1bit也能实现这个功能，因此，作为更好的一种方案，可以只申请大小为8的int类型的数组，由于每个int类型占32bit，所以，大小为8的数组总共为256bit，用1bit来表示一个字符是否已经出现过可以达到同样的目的，实现代码如下：

程序的运行结果如下：

GOOD中有重复字符

算法性能分析：

由于这种方法对字符串进行了一次遍历，因此算法的时间复杂度为O（N）（其中，N是指字符串的长度）。此外，这种方法申请了8个额外的存储空间。

5.13 如何找到由其他单词组成的最长单词

【出自MGYD面试题】

难度系数：★★★★ 被考察系数：★★★☆☆

题目描述：

给定一个字符串数组，找出数组中最长的字符串，使其能由数组中其他的字符串组成。例如给定字符串数组{“test”，“tester”，“testertest”，“testing”，“apple”，“seattle”，“banana”，“batting”，“ngcat”，“batti”，“bat”，“testingtester”，“testbattingcat”}。满足题目要求的字符串为“testbattingcat”，因为这个字符串可以由数组中的字符串“test”、“batti”和“ngcat”组成。

分析与解答：

既然题目要求找最长的字符串，那么可以采用贪心法，首先对字符串由大到小进行排序，从最长的字符串开始查找，如果能由其他字符串组成，就是满足题目要求的字符串。接下来就需要考虑如何判断一个字符串能否由数组中其他的字符串组成，主要的思路是：找出字符串的所有可能的前缀，判断这个前缀是否在字符数组中，如果在，则用相同的方法递归地判断除去前缀后的子串是否能由数组中其他的子串组成。

以题目中给的例子为例，首先对数组进行排序，排序后的结果为{“testbattingcat”，“testingtester”，“testertest”，“testing”，“seattle”，“batting”，“tester”，“banana”，“apple”，“ngcat”，“batti”，“test”，“bat”}。首先取“testbattingcat”进行判断，具体步骤如下：

（1）分别取它的前缀“t”、“te”和“tes”都不在字符数组中，“test”在字符数组中。

（2）接着用相同的方法递归地判断剩余的子串“battingcat”，同理，“b”、“ba”都不在字符数组中，“bat”在字符数组中。

（3）然后判断“tingcat”，通过判断发现“tingcat”不能由字符数组中其他字符组成。因此，回到上一个递归调用的子串接着取字符串的前缀进行判断。

（4）回到上一个递归调用，待判断的字符串为“battingcat”，当前比较到的前缀为“bat”，接着取其他可能的前缀“batt”、“battt”都不在字符数组中，“battti”在字符数组中。接着判断剩余子串“ngcat”。

（5）通过比较发现“ngcat”在字符数组中。因此，能由其他字符组成的最长字符串为“testbattingcat”。

实现代码如下：

程序的运行结果如下：

最长的字符串为：testbattingcat

算法性能分析：

排序的时间复杂度为O（nlog₂ⁿ），假设单词的长度为m，那么有m种前缀，判断一个单词是否在数组中的时间复杂度为O（mn），由于总共有n个字符串，因此，判断所需的时间复杂度为O（m*n^2）。因此，总的时间复杂度为O（nlog₂ⁿm*n^2）。当n比较大的时候，时间复杂度为O（n^2）。

5.14 如何统计字符串中连续的重复字符个数

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

用递归的方法实现一个求字符串中连续出现相同字符的最大值，例如字符串“aaabbcc”中连续出现字符‘a’的最大值为3，字符串“abbc”中连续出现字符‘b’的最大值为2。

分析与解答：

如果不要求采用递归法，那么算法的实现就非常简单，只需要在遍历字符串的时候定义两个额外的变量curMaxLen与maxLen，分别记录与当前遍历的字符重复的连续字符的个数和遍历到目前为止找到的最长的连续重复字符的个数。在遍历的时候，如果相邻的字符相等，则执行curMaxLen+1；否则，更新最长连续重复字符的个数，即maxLen=max（curMaxLen，maxLen），由于碰到了新的字符，因此curMaxLen=1。

题目要求用递归的方法来实现，通过对非递归方法进行分析可以知道，在遍历字符串的时候，curMaxLen与maxLen是最重要的两个变量，那么在进行递归调用的时候，通过传入两个额外的参数（curMaxLen与maxLen）就可以采用与非递归方法类似的方法来实现，实现代码如下：

程序的运行结果如下：

abbc的最长连续重复子串长度为：2

aaabbcc的最长连续重复子串长度为：3

算法性能分析：

由于这种方法对字符串进行了一次遍历，因此算法的时间复杂度为O（N）。这种方法也没有申请额外的存储空间。

5.15 如何求最长递增子序列的长度

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

假设L=＜a1，a2，…，an＞是n个不同的实数的序列，L的递增子序列是这样一个子序列Lin=＜ak1，ak2，…，akm＞，其中，k1＜k2＜…＜km且ak1＜ak2＜…＜akm。求最大的m值。

方法一：最长公共子串法

对序列L=＜a1，a2，…，an＞按递增进行排序得到序列LO=＜b1，b2，…，bn＞。显然，L与LO的最长公共子序列就是L的最长递增子序列。因此，可以使用求公共子序列的方法来求解。

方法二：动态规划法

由于以第i个元素为结尾的最长递增子序列只与以第i-1个元素为结尾的最长递增子序列有关，因此，本题可以采用动态规划的方法来解决。下面首先介绍动态规划方法中的核心内容递归表达式的求解。

以第i个元素为结尾的最长递增子序列的取值有两种可能：

（1）1，第i个元素单独作为一个子串（L[i]＜=L[i-1]）。

（2）以第i-1个元素为结尾的最长递增子序列加1（L[i]＞L[i-1]）。

由此可以得到如下的递归表达式：假设maxLen[i]表示以第i个元素为结尾的最长递增子序列，那么

（1）maxLen[i]=max{1，maxLen[j]+1}，j＜iandL[j]＜L[i]

（2）maxLen[0]=1

根据这个递归表达式可以非常容易地写出实现的代码：

程序的运行结果如下：

xbcdza最长递增子序列的长度为：4

算法性能分析：

由于这种方法用双重循环来实现，因此，这种方法的时间复杂度为O（N^2），此外由于这种方法还使用了N个额外的存储空间，因此，空间复杂度为O（N）。

5.16 求一个串中出现的第一个最长重复子串

【出自TX笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个字符串，找出这个字符串中最长的重复子串，比如给定字符串“banana”，子字符串“ana”出现2次，因此最长的重复子串为“ana”。

分析与解答：

由于题目要求最长重复子串，显然可以先求出所有的子串，然后通过比较各子串是否相等从而求出最长公共子串，具体的思路是：首先找出长度为n-1的所有子串，判断是否有相等的子串，如果有相等的子串，那么就找到了最长的公共子串；否则找出长度为n-2的子串继续判断是否有相等的子串，依次类推直到找到相同的子串或遍历到长度为1的子串为止。这种方法的思路比较简单，但是算法复杂度较高。下面介绍一种效率更高的算法：后缀数组法。

后缀数组是一个字符串的所有后缀的排序数组。后缀是指从某个位置i开始到整个串末尾结束的一个子串。字符串r从第i个字符开始的后缀表示为Suffix（i），也就是Suffix（i）=r[i..len（r）]。例如：字符串“banana”的所有后缀如下：

所以“banana”的后缀数组为{5，3，1，0，4，2}。由此可以把找字符串的重复子串的问题转换为从后缀排序数组中。通过对比相邻的两个子串的公共串的长度。在上例中3：ana与1：anana的最长公共子串为ana。这也就是这个字符串的最长公共子串。实现代码如下：

算法性能分析：

这种方法在生成后缀数组的复杂度为O（N），排序的算法复杂度为O（Nlog2N），最后比较相邻字符串的操作的时间复杂度为O（N），所以算法的时间复杂度为O（Nlog2N）。此外，由于申请了长度为N的额外的存储空间，因此空间复杂度为O（N）。

5.17 如何求解字符串中字典序最大的子序列

【出自MGYD笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个字符串，求串中字典序最大的子序列。字典序最大的子序列是这样构造的：给定字符串a0a1…an-1，首先在字符串a0a1…an-1中找到值最大的字符ai，其次在剩余的字符串ai+1…an-1中找到值最大的字符aj，然后在剩余的aj+1…an-1中找到值最大的字符ak…直到字符串的长度为0，则aiajak…即为答案。

分析与解答：

方法一：顺序遍历法

最直观的思路就是首先遍历一次字符串，找出最大的字符ai，接着从ai开始遍历再找出最大的字符，依此类推直到字符串长度为0。

以"acbdxmng"为例，首先对字符串遍历一遍，找出最大的字符‘x’；接着从‘m’开始遍历，找出最大的字符‘n’；然后从‘g’开始遍历，找到最大的字符‘g’。因此“acbdxmng”的最大子序列为“xng”。实现代码如下：

程序的运行结果如下：

xng

算法性能分析：

这种方法在最坏情况下（字符串中的字符按降序排列）的时间复杂度为O（n^2）；在最好情况下（字符串中的字符按升序排列）的时间复杂度为O（n）。此外这种方法需要申请n+1个额外的存储空间，因此，空间复杂度为O（n）。

方法一：逆序遍历法

通过对上述运行结果进行分析，发现an-1^一定在所求的子串中，接着逆序遍历字符串，大于或等于an-1的字符也一定在子串中，依次类推，一直往前遍历，只要遍历到的字符大于或等于子串首字符，就把这个字符加到子串首。由于这种方法首先找到的是子串的最后一个字符，最后找到的是子串的第一个字符，因此，在实现的时候首先按照找到字符的顺序把找到的字符保存到数组中，最后再对字符数组进行逆序，从而得到要求的字符。以"acbdxmng"为例，首先，字符串的最后一个字符‘g’一定在子串中，接着逆向遍历找到大于或等于‘g’的字符‘n’加入到子串中“gn”（子串的首字符为‘n’），接着继续逆向遍历找到大于或等于‘n’的字符‘x’加入到子串中“gnx”，接着继续遍历，没有找到比‘x’大的字符。最后对子串“gnx”逆序得到“xng”。实现代码如下：

算法性能分析：

这种方法只需要对字符串遍历一次，因此，时间复杂度为O（n）。此外，这种方法需要申请n+1个额外的存储空间，因此空间复杂度为O（n）。

5.18 如何判断一个字符串是否由另外一个字符串旋转得到

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个能判断一个单词是否为另一个单词的子字符串的方法，记为isSubstring。如何判断s2是否能通过旋转s1得到（只能使用一次isSubstring方法）。例如：“waterbottle”可以通过字符串“erbottlewat”旋转得到。

分析与解答：

如果题目没有对isString使用的限制，可以通过求出s2进行旋转的所有组合，然后与s1进行比较。但是这种方法的时间复杂度比较高。通过对字符串旋转进行仔细分析，发现对字符串s1进行旋转得到的字符串一定是s1s1的子串。因此可以通过判断s2是否是s1s1的子串来判断s2能够通过旋转s1得到。例如：s1=“waterbottle”，那么s1s1=“waterbottlewaterbottle”，显然s2是s1s1的子串，因此s2能通过旋转s1得到。实现代码如下：

程序的运行结果如下：

erbottlewat可以通过旋转waterbottle得到

为了简单起见，这种方法中isSubstring通过调用库函数的方式进行了实现，当然在采用KMP算法实现的isSubstring的效率最高。

算法性能分析：

这种方法首先对字符串str1进行了一次遍历，时间复杂度为O（N）（其中，N为字符串的长度），接着调用了isSubstring函数（假设采用了KMP算法），这种方法的时间复杂度为O（2N+N）=O（3N），因此，整个算法的时间复杂度为O（N）。此外这种方法申请了2N+1个存储空间，因此，算法的空间复杂度也为O（N）。

5.19 如何求字符串的编辑距离

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

编辑距离又称Levenshtein距离，是指两个字符串之间由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符、插入一个字符或删除一个字符。请设计并实现一个算法来计算两个字符串的编辑距离，并计算其复杂度。在某些应用场景下，替换操作的代价比较高，假设替换操作的代价是插入和删除的两倍，算法该如何调整？

分析与解答：

本题可以使用动态规划的方法来解决，具体思路如下：

给定字符串s1和s2，首先定义一个函数D（i，j）（0＜=i＜=strlen（s1），0＜=j＜=strlen（s2）），用来表示第一个字符串s1长度为i的子串与第二个字符串s2长度为j的子串的编辑距离。从s1变到s2可以通过如下三种操作实现：

（1）添加操作。假设已经计算出D（i，j-1）的值（s1[0…i]与s2[0…j-1]的编辑距离），则D（i，j）=D（i，j-1）+1（s1长度为i的字串后面添加s2[j]即可）。

（2）删除操作。假设已经计算出D（i-1，j）的值（s1[0…i-1]到s2[0…j]的编辑距离），则D（i，j）=D（i-1，j）+1（s1长度为i的字串删除最后的字符s1[j]即可）。

（3）替换操作。假设已经计算出D（i-1，j-1）的值（s1[0…i-1]与s2[0…j-1]的编辑距离），如果s1[i]=s2[j]，则D（i，j）=D（i-1，j-1），如果s1[i]！=s2[j]，则D（i，j）=D（i-1，j-1）+1（替换s1[i]为s2[j]，或替换s2[j]为s1[i]）。

此外，D（0，j）=j且D（i，0）=i（从一个字符串变成长度为0的字符串的代价为这个字符串的长度）。

由此可以得出如下实现方式：对于给定的字符串s1和s2，定义一个二维数组D，则有以下几种可能性。

（1）如果i==0，那么D[i，j]=j（0＜=j＜=strlen（s2））。

（2）如果j==0，那么D[i，j]=i（0＜=i＜=strlen（s1））。

（3）如果i＞0且j＞0，

（a）如果s1[i]==s2[j]，那么D（i，j）=min{edit（i-1，j）+1，edit（i，j-1）+1，edit（i-1，j-1）}。

（b）如果s1[i]！=s2[j]，那么D（i，j）=min{edit（i-1，j）+1，edit（i，j-1）+1，edit（i-1，j-1）+1}。

通过以上分析可以发现，对于第一个问题可以直接采用上述的方法来解决。对于第二个问题，由于替换操作是插入或删除操作的两倍，因此只需要修改如下条件即可：

如果s1[i]！=s2[j]，那么D（i，j）=min{edit（i-1，j）+1，edit（i，j-1）+1，edit（i-1，j-1）+2}。

根据上述分析，给出实现代码如下：

程序运行结果如下：

算法性能分析：

这种方法的时间复杂度与空间复杂度都为O（m*n）（其中，m和n分别为两个字符串的长度）。

5.20 如何在二维数组中寻找最短路线

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

寻找一条从左上角（arr[0][0]）到右下角（arr[m-1][n-1]）的路线，使得沿途经过的数组中的整数的和最小。

分析与解答：

对于这道题，可以从右下角开始倒着来分析这个问题：最后一步到达arr[m-1][n-1]只有两条路：通过arr[m-2][n-1]到达或通过arr[m-1][n-2]到达，假设从arr[0][0]到arr[m-2][n-1]沿途数组最小值为f（m-2，n-1），到arr[m-1][n-2]沿途数组最小值为f（m-1，n-2）。因此，最后一步选择的路线为min{f（m-2，n-1），f（m-1，n-2）}。同理，选择到arr[m-2][n-1]或arr[m-1][n-2]的路径可以采用同样的方式来确定。

由此可以推广到一般的情况。假设到arr[i-1][j]与arr[i][j-1]的最短路径的和为f（i-1，j）和f（i，j-1），那么到达arr[i][j]的路径的上所有数字和的最小值为f（i，j）=min{f（i-1，j），f（i，j-1）}+arr[i][j]。

方法一：递归法

根据这个递归公式可知，可以采用递归的方法来实现，递归的结束条件为遍历到arr[0][0]。在求解的过程中还需要考虑另外一种特殊情况：遍历到arr[i][j]（当i=0或j=0）的时候，只能沿着一条固定的路径倒着往回走直到arr[0][0]。根据这个递归公式与递归结束条件可以给出实现代码如下：

程序的运行结果如下：

17

这种方法虽然能得到题目想要的结果，但是效率太低，主要是因为里面有大量的重复计算过程，比如在计算f（i-1，j）与f（j-1，i）的过程中都会计算f（i-1，j-1）。如果把第一次计算得到的f（i-1，j-1）缓存起来就不需要额外的计算了，而这也是典型的动态规划的思路，下面重点介绍动态规划方法。

方法2：动态规划法

动态规划法其实也是一种空间换时间的算法，通过缓存计算中间值，从而减少重复计算的次数，从而提高算法的效率。方法1从arr[m-1][n-1]开始逆向通过递归来求解，而动态规划要求正向求解，以便利用前面计算出来的结果。

对于本题而言，显然，f（i，0）=arr[0][0]+…+arr[i][0]，f[0，j]=arr[0][0]+…+arr[0][j]。根据递推公式：f（i，j）=min{f（i-1，j），f（i，j-1）}+arr[i][j]，从i=1，j=1开始顺序遍历二维数组，可以在遍历的过程中求出所有的f（i，j）的值，同时，把求出的值保存到另外一个二维数组中以供后续使用。当然在遍历的过程中可以确定这个最小值对应的路线，在这种方法中，除了求出最小值以外顺便还打印出了最小值的路线，实现代码如下：

程序的运行结果如下：

路径：[0，1] [0，2] [2，0] [2，1] [2，2]

最小值为：17

算法性能分析：

这种方法对二维数组进行了一次遍历，因此其时间复杂度为O（m*n）。此外由于这种方法同样申请了一个二维数组来保存中间结果，因此其空间复杂度也为O（m*n）。

5.21 如何截取包含中文的字符串

【出自MT面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

编写一个截取字符串的函数，输入为一个字符串和字节数，输出为按字节截取的字符串。但是要保证汉字不被截半个，例如"人ABC"4，应该截为"人AB"，输入"人ABC们DEF"，6，应该输出为"人ABC"而不是"人ABC+们的半个"。

分析与解答：

在Java语言中，默认使用的Unicode编码方式，即每个字符占用2字节，因此可以用来存储中文。虽然String是由char所组成的，但是它采用了一种更加灵活的方式来存储，即英文占用一个字符，中文占用两个字符，采用这种存储方式的一个重要作用就是可以减少所需的存储空间，提高存储效率。根据这个特点，可以采用如下代码来完成题目的要求：

程序的运行结果如下：

人ABC

5.22 如何求相对路径

【出自SLL笔试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

编写一个函数，根据两个文件的绝对路径算出其相对路径。例如

a="/qihoo/app/a/b/c/d/new.c"，b="/qihoo/app/1/2/test.c"，那么b相对于a的相对路径是"../../../../1/2/test.c"

分析与解答：

首先找到两个字符串相同的路径（/aihoo/app），然后处理不同的目录结构（a="/a/b/c/d/new.c"，b="/1/2/test.c"）。处理方法为：对于a中的每一个目录结构，在b前面加“../”，对于本题而言，除了相同的目录前缀外，a还有四级目录a/b/c/d，因此只需要在b="/1/2/test.c"前面增加四个"../"得到的"../../../../1/2/test.c"就是b相对a的路径。实现代码如下：

程序的运行结果如下：

../../../../1/2/test.c

算法性能分析：

这种方法的时间复杂度与空间复杂度都为O（max（m，n））（其中，m和n分别为两个路径的长度）。

5.23 如何查找到达目标词的最短链长度

【出自JD面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

给定一个字典和两个长度相同的“开始”和“目标”的单词。找到从“开始”到“目标”最小链的长度。如果它存在，那么这条链中的相邻单词只有一个字符不同，而链中的每个单词都是有效的单词，即它存在于字典中。可以假设词典中存在“目标”字，所有词典词的长度相同。

例如：

给定一个单词字典为{pooN，pbcc，zamc，poIc，pbca，pbIc，poIN}

start=TooN

target=pbca

输出结果为7

因为TooN（start）-pooN-poIN-poIc-pbIc-pbcc-pbca（target）。

分析与解答：

本题主要的解决方法是：使用BFS的方式从给定的字符串开始遍历所有相邻（两个单词只有一个不同的字符）的单词，直到遍历找到目标单词或者遍历完所有的单词为止。实现代

码如下：

程序的运行结果为

最短的链条的长度为7

算法性能分析：

这种方法的时间复杂度为为O（n²m），其中，n为单词的个数，m为字符串的长度。

第6章 基本数字运算

计算机软件技术与数学是不可切割的有机整体，很多企业在招聘求职者的时候，往往非常在意求职者的数学能力，站在企业的角度来看，编程语言是很简单的东西，只要熟悉一种语言，其他语言也很容易学会，而数学素养的高低却不然，需要长时间的学习与积累，直接决定了未来求职者的职业生涯的发展。所以，面试官在考察求职者时也比较喜欢出此类题目。

6.1 如何判断一个自然数是否是某个数的平方

【出自GG面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

设计一个算法，判断给定的一个数n是否是某个数的平方，不能使用开方运算。例如16就满足条件，因为它是4的平方；而15则不满足条件，因为不存在一个数使得其平方值为15。

分析与解答：

方法一：直接计算法

由于不能使用开方运算，因此最直接的方法就是计算平方。主要思路：对1到n的每个数i，计算它的平方m，如果m＜n，则继续遍历下一个值（i+1），如果m==n，那么说明n是m的平方，如果m＞n，那么说明n不能表示成某个数的平方。实现代码如下：

程序的运行结果如下：

15不是某个自然数的平方

16是某个自然数的平方

算法性能分析：

由于这种方法只需要从1遍历到n^0.5就可以得出结果，因此算法的时间复杂度为O（n^0.5）。

方法二：二分查找法

与方法一类似，这种方法的主要思路还是查找从1～n的数字中，是否存在一个数m，使得m的平方为n。只不过在查找的过程中使用的是二分查找的方法。具体思路是：首先判断mid=（1+n）/2的平方power与m的大小，如果power＞m，那么说明在[1，mid-1]区间继续查找，否则在[mid+1，n]区间继续查找。

实现代码如下：

算法性能分析：

由于这种方法使用了二分查找的方法，因此，时间复杂度为O（log₂ⁿ），其中，n为数的大小。

方法三：减法运算法

通过对平方数进行分析发现有如下规律：

（n+1）^2=n^2+2n+1=（n-1）^2+（2*（n-1）+1）+2*n+1=…=1+（2*1+1）+（2*2+1）+…+（2*n+1）。通过上述公式可以发现，这些项构成了一个公差为2的等差数列的和。由此可以得到如下的解决方法：对n依次减1，3，5，7，…，如果相减后的值大于0，则继续减下一项；如果相减后的值等于0，则说明n是某个数的平方；如果相减的值小于0，则说明n不是某个数的平方。根据这个思路，代码实现如下：

算法性能分析：

这种方法的时间复杂度仍然为O（n^0.5）。由于方法一使用的是乘法操作，这种方法采用的是减法操作，因此这种方法的执行效率比方法一更高。

6.2 如何判断一个数是否为2的n次方

【出自ALBB面试题】

难度系数：★★★☆☆ 被考察系数：★★★★★

分析与解答：

方法一：构造法

2的n次方可以表示为2^0，2^1，2^2，2^n，如果一个数是2的n次方，那么最直观的的想法是对1执行了移位操作（每次左移一位），即通过移位得到的值必定是2的n次方（针对n的所有取值构造出所有可能的值）。所以，要想判断一个数是否为2的n次方，只需要判断该数移位后的值是否与给定的数相等，实现代码如下：

程序的运行结果如下：

8能表示成2的n次方

9不能表示成2的n次方

算法性能分析：

上述算法的时间复杂度为O（（log2ⁿ）。

方法二：与操作法

那么是否存在效率更高的算法呢？通过对2^0，2^1，2^2，…，2^n进行分析，发现这些数字的二进制形式分别为：1，10，100，…。从二进制的表示可以看出，如果一个数是2的n次方，那么这个数对应的二进制表示中有且只有一位是1，其余位都为0。因此，判断一个数是否为2的n次方可以转换为这个数对应的二进制表示中是否只有一位为1。如果一个数的二进制表示中只有一位是1，例如num=00010000，那么num-1的二进制表示为num-1=00001111，由于num与num-1二进制表示中每一位都不相同，因此，num&（num-1）的运算结果为0。可以利用这种方法来判断一个数是否为2的n次方。实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（1）。

6.3 如何不使用除法操作符实现两个正整数的除法

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

分析与解答：

方法一：减法

主要思路是：使被除数不断减去除数，直到相减的结果小于除数为止，此时，商就为相减的次数，余数为最后相减的差。例如在计算14除以4的时候，首先计算14-4=10，由于10＞4，继续做减法运算：10-4=6，6-4=2，此时2＜4。由于总共进行了3次减法操作，最终相减的结果为2，因此，15除以4的商为3，余数为2。如果被除数比除数都小，那么商为0，余数为被除数。根据这个思路的实现代码如下：

程序的运行结果如下：

14除以4商为：3余数为2

算法性能分析：

这种方法循环的次数为m/n，因此算法的时间复杂度为O（m/n）。需要注意的是，这种方法也实现了不用%操作符实现%运算的目的。

方法二：移位法

方法一所采用的减法操作，还可以用等价的加法操作来实现。例如在计算17除以4的时候，可以尝试4*1，4*2（4+4），4*3（4+4+4）依次进行计算，直到计算的结果大于14的时候就可以很容易地求出商与余数。但是这种方法每次都递增4，效率较低。下面给出另外一种增加递增速度的方法：以2的指数进行递增（取2的指数的原因是，2的指数操作可以通过移位操作来实现，有更高的效率），计算4*1，4*2，4*4，4*8，由于4*8＞17，然后接着对17-4*4=1进入下一次循环用相同的方法进行计算。实现代码如下：

算法性能分析：

由于这种方法采用指数级的增长方式不断逼近m/n，因此算法的时间复杂度为O（log（m/n））。

引申一：如何不用加减乘除运算实现加法

分析与解答：

由于不能使用加减乘除运算，因此只能使用位运算了。首先通过分析十进制加法的规律来找出二进制加法的规律，从而把加法操作转换为二进制的操作来完成。

十进制的加法运算过程可以分为以下3个步骤：

（1）各个位相加而不考虑进位，计算相加的结果sum。

（2）只计算各个位相加时进位的值carry。

（3）将sum与carry相加就可以得到这两个数相加的结果。

例如15+29的计算方法为sum=34（不考虑进位），carry=10（只计算进位），因此，15+29=sum+carry=34+10=44。

同理，二进制加法与十进制加法有着相似的原理，唯一不同的是，在二进制加法中，sum与carry的和可能还有进位，因此在二进制加法中会不停地执行sum+carry操作，直到没有进位为止。具体实现方法如下：

（1）二进制各个位相加而不考虑进位。由于在不考虑进位的时候加法操作可以用异或操作代替，因此，不考虑进位的加法可以用异或运算来代替。

（2）计算进位，由于只有1+1才会产生进位，因此进位的计算可以用与操作代替。进位的计算方法为：先做与运算，再把运算结果左移一位。

（3）不断对（1）、（2）两步得到的结果相加，直到进位为0的时候为止。

根据这个思路实现代码如下：

程序的运行结果为

6

引申二：如何不用加减乘除运算实现减法

分析与解答：

由于减去一个数等于加上这个数的相反数，即-n=～（n-1）=～n+1，因此，a-b=a+（-b）=a+（～b）+1，可以利用上面已经实现的加法操作来实现减法操作，实现代码如下：

引申三：如何不用加减乘除运算实现乘法

分析与解答：

以11*14为例介绍乘法运算的规律，11的二进制可以表示为1011，14的二进制可以表示为1110，二进制相乘的运算过程如下：

二进制数10011010的十进制表示为154=11*14，从这个例子可以看出，乘法运算可以转换为加法运算。计算a*b的主要思路是：（1）初始化运算结果为0，sum=0。（2）找到b对应二进制中最后一个1的位置i（位置编号从右到左依次为0，1，2，3…），并去掉这个1。（3）执行加法操作sum+=a＜i。（4）循环执行（1）、（2）和（3）步，直到b对应的二进制数中没有更多的1为止。

从6.2节中可知，对n执行n&（n-1）操作可以去掉n的二进制数表示中的最后一位1，因此n&～（n-1）的结果为只保留n的二进制数中的最后一位1。因此可以通过n&～（n-1）找出n中最后一个1的位置，然后通过n&（n-1）去掉最后一个1。在上述的第（2）步中，首先执行lastBit=n&～（n-1），得到的值lastBit只包含n对应的二进制表示中最后一位1，要想确定1的位置，需要通过对1不断进行左移操作，直到移位的结果等于lastBit时移位的次数就是位置编号。在实现的时候，为了提高程序的运行效率，可以把1向左移动的位数（0，1，2，3…31）先计算好并保存起来。实现代码如下：

引申四：另外一种除法的实现方式

分析与解答：

由于除法是乘法的逆运算，因此，可以很容易地将除法运算转换为乘法运算，实现代码如下：

6.4 如何只使用++操作符实现加减乘除运算

【出自XL笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

分析与解答：

本题要求只能使用++操作来实现加减乘除运算，下面重点介绍用++操作来实现加减乘除运算的方法：

（1）加法操作：实现a+b的基本思路为对a执行b次++操作即可。

（2）减法操作：实现a-b（a＞=b）的基本思路是：不断对b执行++操作，直到等于a为止，在这个过程中记录执行++操作的次数。

（3）乘法操作：实现a*b的基本思路是：利用已经实现的加法操作把a相加b次，就得到了a*b的值。

（4）除法操作：实现a/b的基本思路是：利用乘法操作，使b不断乘以1，2，…n，直到b*n＞b时，就可以得到商为n-1。

根据以上思路，实现代码如下：

程序的运行结果如下：

-2

6

8

2

此外，在实现加法操作的时候，如果a与b都是整数，那么可以选择比较小的数进行循环，从而可以提高算法的性能。

6.5 如何根据已知随机数生成函数计算新的随机数

【出自GG面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

已知随机数生成函数rand7（）能产生的随机数是整数1～7的均匀分布，如何构造rand10（）函数，使其产生的随机数是整数1～10的均匀分布。

分析与解答：

要保证rand10（）产生的随机数是整数1～10的均匀分布，可以构造一个1～10*n的均匀分布的随机整数区间（n为任何正整数）。假设x是这个1～10*n区间上的一个随机数，那么x%10+1就是均匀分布在1～10区间上的整数。

根据题意，rand7（）函数返回1～7的随机数，那么rand7（）-1则得到一个离散整数集合，该集合为{0，1，2，3，4，5，6}，该集合中每个整数的出现概率都为1/7。那么（rand7（）-1）*7得到另一个离散整数集合A，该集合元素为7的整数倍，即A={0，7，14，21，28，35，42}，其中，每个整数的出现概率也都为1/7。而由于rand7（）得到的集合B={1，2，3，4，5，6，7}，其中每个整数出现的概率也为1/7。显然集合A与集合B中任何两个元素和组合可以与1～49之间的一个整数一一对应，即1～49之间的任何一个数，可以唯一地确定A和B中两个元素的一种组合方式，这个结论反过来也成立。由于集合A和集合B中元素可以看成是独立事件，根据独立事件的概率公式P（AB）=P（A）P（B），得到每个组合的概率是1/7*1/7=1/49。因此，（rand7（）-1）*7+rand7（）生成的整数均匀分布在1～49之间，而且，每个数的概率都是1/49。

所以，（rand7（）-1）*7+rand7（）可以构造出均匀分布在1～49的随机数，为了将49种组合映射为1～10之间的10种随机数，就需要进行截断了，即将41～49这样的随机数剔除掉，得到的数1～40仍然是均匀分布在1～40的，这是因为每个数都可以看成一个独立事件。由1～40区间上的一个随机数x，可以得到x%10+1就是均匀分布在1～10区间上的整数。

程序代码如下：

程序的运行结果如下：

6 10 8 1 8 6 3 8 10 7

6.6 如何判断1024！末尾有多少个0

【出自GG面试题】

难度系数：★★★★ 被考察系数：★★★★☆

分析与解答：

方法一：蛮力法

最简单的方法就是计算出1024！的值，然后判断末尾有多少个0，但是这种方法有两个非常大的缺点：第一，算法的效率非常低；第二，当这个数字比较大的时候直接计算阶乘可能会导致数据溢出，从而导致计算结果出现偏差。因此，下面给出一种比较巧妙的方法。

方法二：因子法

5与任何一个偶数相乘都会增加末尾0的个数，由于偶数的个数肯定比5的个数多，因此，1～1024所有数字中有5的因子的数字的个数决定了1024！末尾0的个数。因此，只需要统计因子5的个数即可。此外5与偶数相乘会使末尾增加一个0，25（有两个因子5）与偶数相乘会使末尾增加两个0，125（有三个因子5）与偶数相乘会使末尾增加3个0，625（有四个因子5）与偶数相乘会使末尾增加四个0。对于本题而言：

是5的倍数的数有：a1=1024/5=204个

是25的倍数的数有：a2=1024/25=40个（a1计算了25中的一个因子5）

是125的倍数的数有：a3=1024/125=8个（a1，a2分别计算了125中的一个因子5）

是625的倍数的数有：a4=1024/625=1个（a1，a2，a3分别计算了625中的一个因子5）

所以，1024！中总共有a1+a2+a3+a4=204+40+8+1=253个因子5。因此，末尾总共有253个0。根据以上思路实现代码如下：

程序的运行结果如下：

1024！末尾0的个数为：253

算法性能分析：

由于这种方法循环的次数为n/5，因此，算法时间复杂度为O（N）。

引申：如何计算N！末尾有几个0

分析与解答：

从以上的分析可以得出N！末尾0的个数为N/5+N/5^2+N/5^3+N/5^m（5^m＜N且5^（m+1）＞N）。

6.7 如何按要求比较两个数的大小

【出自TX笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

如何比较a、b两个数的大小（返回最大值），不能使用大于、小于。

分析与解答：

方法一：绝对值法

根据绝对值的性质可知，如果|a-b|==a-b，那么max（a，b）=a，否则max（a，b）=b，根据这个思路实现代码如下：

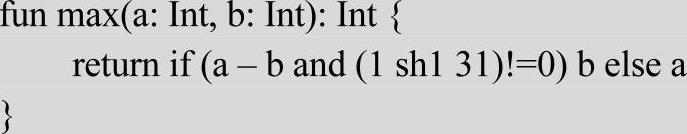
或

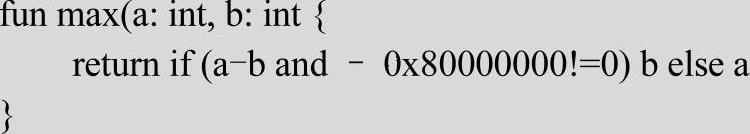
程序的运行结果如下：

6

需要注意的是，由于宏定义不同于函数定义，在上述宏定义中，a、b必须要有括号，否则当a、b的值为表达式的时候会出现意想不到的错误。

方法二：二进制法

如果a＞b，那么a-b的二进制最高位为0，与任何数的与操作的结果还是0；如果a-b为负数，那么a-b的二进制最高位为1，与0x80000000（最高位为1，其他位为0，假设a与b都占4个字节）执行与操作之后为结果为1。由此根据两个数的差的二进制最高位的值就可以比较两个数的大小，实现方法如下：

（（a-b）&（1＜＜31））！=0？b：a

或

（（（a-b））&0x80000000）！=0？b：a

6.8 如何求有序数列的第1500个数的值

【出自WR面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

一个有序数列，序列中的每一个值都能够被2或者3或者5所整除，求第1500个值是多少。

分析与解答：

方法一：蛮力法

最简单的方法就是用一个计数器来记录满足条件的整数的个数，然后从1开始遍历整数，如果当前遍历的数能被2或者3或者5整除，则计数器的值加1，当计数器的值为1500时，当前遍历到的值就是所要求的值。根据这个思路实现代码如下：

程序的运行结果如下：

2045

方法二：数字规律法

首先可以很容易得到2、3和5的最小公倍数为30，此外，1～30这个区间内满足条件的数有22个{2，3，4，5，6，8，9，10，12，14，15，16，18，20，21，22，24，25，26，27，28，30}，由于最小公倍数为30，可以猜想，满足条件的数字是否具有周期性（周期为30）呢？通过计算可以发现，31～60这个区间内满足条件的数也恰好有22个{32，33，34，35，36，38，39，40，42，44，45，46，48，50，51，52，54，55，56，57，58，60}，从而发现这些满足条件的数具有周期性（周期为30）。由于1500/22=68，1500%68=4，从而可以得出第1500个数经过了68个周期，然后在第69个周期中取第四个满足条件的数{2，3，4，5}。从而可以得出第1500个数为68*30+5=2045。根据这个思路实现代码如下：

算法性能分析：

方法二的时间复杂度为O（1），此外，方法二使用了22个额外的存储空间。方法二的计算方法可以用来分析方法一的执行效率，从方法二的实现代码可以得出，方法一中循环执行的次数为（N/22）*30+a[N%22]，其中，a[N%22]的取值范围为2～30，因此方法一的时间复杂度为O（N）。

6.9 如何把十进制数（long型）分别以二进制和十六进制形式输出

【出自YH面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

分析与解答：

由于十进制数本质上还是以二进制的方式来存储的，在实现的时候可以把十进制数看成二进制的格式，通过移位的方式计算出每一位的值。为了方便起见，下面以byte类型的数为例介绍实现方法。假如现在要把十进制数7以二进制的形式来输出，由于7的二进制的表示为00000111，计算第6位二进制码是0还是1的方法是：首先把这个值左移6位得到11000000，然后再右移7位，得到00000001，移位后得到的值就是第6位二进制码的值。由此可以得出如下计算方法：假设十进制数对应的二进制数的长度为binNum，那么计算十进制数n的第i位二进制码值的公式为n＜＜i＞＞binNum-1。通过这种计算方法可以得到每一位的值，然后把对应的值存储在字符数组中即可。

上面介绍的方法使用的是移位操作，虽然效率比较高，但是难以理解。下面介绍一种简单的转换为十六进制的方法。可以使用类似于十进制转二进制的方法。把十进制的数对16求余数。得到的余数就是十六进制的最后一位，然后把这个十进制数除以16，用得到的数继续使用相同的方法计算其他的位数。需要注意的是对于十六进制10～15需要转换为A～F。示例代码如下所示：

程序的运行结果如下：

10的二进制输出为：0000000000000000000000000000000000000000000000000000000000001010

10的十六进制输出为：A

6.10 如何求二进制数中1的个数

【出自TX笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个整数，输出这个整数的二进制表示中1的个数。例如：给定整数7，其二进制表示为111，因此输出结果为3。

分析与解答：

方法一：移位法

可以采用位操作来完成。具体思路如下：首先，判断这个数的最后一位是否为1，如果为1，则计数器加1，然后，通过右移丢弃掉最后一位，循环执行该操作直到这个数等于0为止。在判断二进制表示的最后一位是否为1时，可以采用与运算来达到这个目的。具体实现

代码如下：

程序的运行结果如下：

3

1

算法性能分析：

这种方法的时间复杂度为O（N），其中，N代表二进制数的位数。

方法二：与操作法

给定一个数n，每进行一次n&（n-1）计算，其结果中都会少了一位1，而且是最后一位。例如，n=6，其对应的二进制表示为110，n-1=5，对应的二进制表示为101，n&（n-1）运算后的二进制表示为100，其效果就是去掉了110中最后一位1。可以通过不断地用n&（n-1）操作去掉n中最后一位1的方法求出n中1的个数，实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（m），其中，m为二进制数中1的个数，显然，当二进制数中1的个数比较少的时候，这种方法有更高的效率。

6.11 如何找最小的不重复数

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定任意一个正整数，求比这个数大且最小的“不重复数”。“不重复数”的含义是相邻两位不相同，例如1101是重复数，而1201是不重复数。

分析与解答：

方法一：蛮力法

最容易想到的方法就是对这个给定的数加1，然后判断这个数是不是“不重复数”，如果不是，则继续加1，直到找到“不重复数”为止。显然这种方法的效率非常低。

方法二：从右到左的贪心法

例如给定数字11099，首先对这个数字加1，变为11000，接着从右向左找出第一对重复的数字00，对这个数字加1，变为11001，继续从右向左找出下一对重复的数00，将其加1，同时把这一位往后的数字变为0101…串（当某个数字自增后，只有把后面的数字变成0101…，才是最小的不重复数字），这个数字变为11010，接着采用同样的方法，11010-＞12010就可以得到满足条件的数。

需要特别注意的是，当对第i个数进行加1操作后可能会导致第i个数与第i+1个数相等，因此，需要处理这种特殊情况，下图以99020为例介绍处理方法。

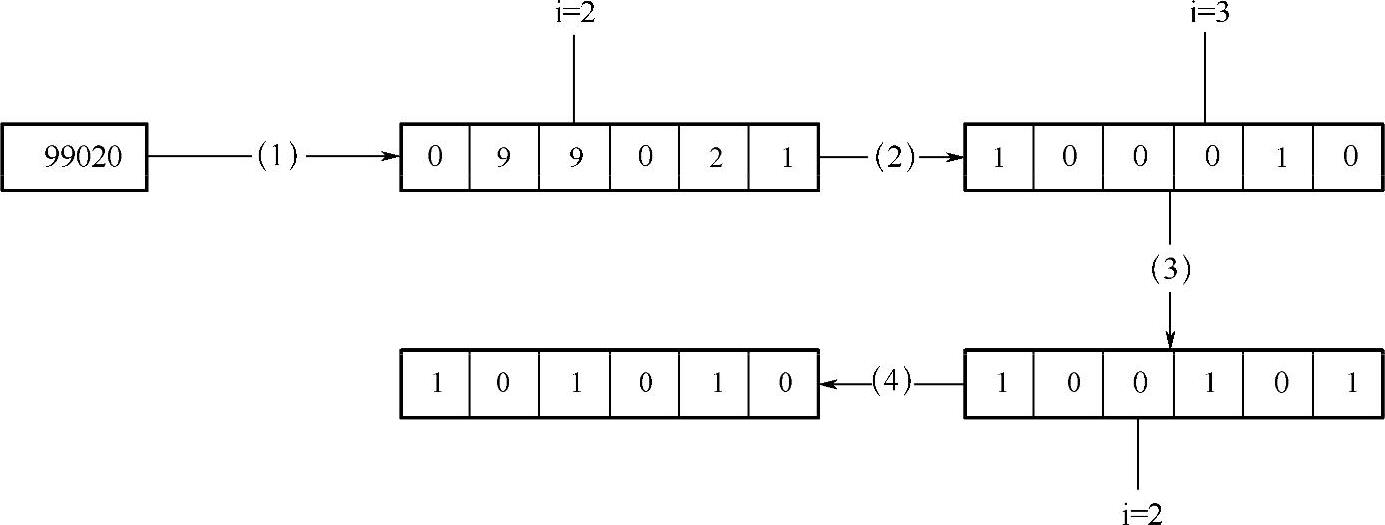
（1）把数字加1并转换为字符串。

（2）从右到左找到第一组重复的数99（数组下标为i=2），然后把99加1，变为100，然后把后面的字符变为0101…串。得到100010。

（3）由于执行步骤（2）后对下标为2的值进行了修改，导致它与下标为i=3的值相同，因此，需要对i自增变为i=3，接着从i=3开始从右向左找出下一组重复的数字00，对00加1变为01，后面的字符变为0101…串，得到100101。

（4）由于下标为i=3与i+1=4的值不同，因此，可以从i-1=2的位置开始从右向左找出下一组重复的数字00，对其加1就可以得到满足条件的最小的“不重复数”。

根据这个思路给出实现方法如下：

1）对给定的数加1。

2）循环执行如下操作：对给定的数从右向左找出第一对重复的数（下标为i），对这个数字加1，然后把这个数字后面的数变为0101…得到新的数。如果操作结束后下标为i的值等于下标为i+1的值，则对i进行自增，否则对i进行自减；然后从下标为i开始从右向左重复执行步骤2），直到这个数是“不重复数”为止。

实现代码如下：

程序的运行结果如下：

循环次数为：7

23401

循环次数为：11

1201010

循环次数为：13

101010

循环次数为：10

9010

方法三：从左到右的贪心法

与方法二类似，只不过是从左到右开始遍历，如果碰到重复的数字，则把其加1，后面的数字变成0101…串。实现代码如下：

显然，方法三循环的次数少于方法二，因此，方法三的性能要优于方法二。

6.12 如何计算一个数的n次方

【出自WR面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

给定一个数d和n，如何计算d的n次方？例如：d=2，n=3，d的n次方为2^3=8。

分析与解答：

方法一：蛮力法

可以把n的取值分为如下几种情况：

（1）n=0，那么计算结果肯定为1。

（2）n=1，计算结果肯定为d。

（3）n＞0，计算方法为：初始化计算结果result=1，然后对result执行n次乘以d的操作，得到的结果就是d的n次方。

（4）n＜0，计算方法为：初始化计算结果result=1，然后对result执行|n|次除以d的操作，得到的结果就是d的n次方。

以2的3次方为例，首先初始化result=1，接着对result执行三次乘以2的操作：result=result*2=1*2=2，result=result*2=2*2=4，result=result*2=4*2=8，因此，2的3次方等于8。根据这个思路给出实现代码如下：

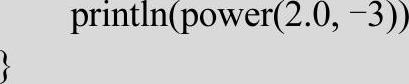
程序的运行结果如下：

8

-8

0.125

算法性能分析：

这种方法的时间复杂度为O（n），需要注意的是，当n非常大的时候，这种方法的效率是非常低的。

方法二：递归法

由于方法一没有充分利用中间的计算结果，因此，算法效率还有很大的提升余地。例如在计算2的100次方的时候，假如已经计算出了2的50次方的值tmp=2^50，就没必要对tmp再乘以50次2，可以直接利用tmp*tmp就得到了2^100的值。可以利用这个特点给出递归实现方法如下：

（1）n=0，那么计算结果肯定为1。

（2）n=1，计算结果肯定为d。

（3）n＞0，首先计算2^（n/2）的值tmp，如果n为奇数，那么计算结果result=tmp*tmp*d，如果n为偶数，那么计算结果result=tmp*tmp。

（4）n＜0，首先计算2^（|n/2|）的值tmp，如果n为奇数，那么计算结果result=1/（tmp*tmp*d），如果n为偶数，那么计算结果result=1/（tmp*tmp）。

根据以上思路实现代码如下：

算法性能分析：

这种方法的时间复杂度为O（（log2ⁿ）。

6.13 如何在不能使用库函数的条件下计算n的平方根

【出自ALBB面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定一个数n，求出它的平方根，比如16的平方根为4。要求不能使用库函数。

分析与解答：

正数n的平方根可以通过计算一系列近似值来获得，每个近似值都比前一个更加接近准确值，直到找出满足精度要求的那个数位置。具体而言，可以找出第一个近似值是1，接下来的近似值则可以通过下面的公式来获得：a_i+1=（a_i+n/a_i）/2。实现代码如下：

程序的运行结果如下：

50的平方根为7.071068

4的平方根为2.000000

6.14如何不使用^操作实现异或运算

【出自YMX面试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

不使用^操作实现异或运算。

分析与解答：

最简单的方法是遍历两个整数的所有的位，如果两个数的某一位相等，那么结果中这一位的值为0，否则结果中这一位的值为1，实现代码如下：

程序的运行结果如下：

6

下面介绍另外一种更加简洁的实现方法：x^y=（x|y）&（～x|～y），其中x|y表示如果在x或y中的bit为1，那么结果的这一个bit的值也为1，显然这个结果包括三部分：这个bit只有在x中为1，只有在y中为1，在x和y中都为1，要在这个基础上计算出异或的结果，显然要去掉第三种情况，也就是说去掉在x和y中都为1的情况，而当一个bit在x和y中都为1的时候“～x|～y”的值为0，因此（x|y）&（～x|～y）的值等于x^y。实现代码如下：

funxor（x：Int，y：Int）：Int{

returnxoryand（x.inv（）ory.inv（））

}

算法性能分析：

这种方法的时间复杂度为O（N）。

6.15 如何不使用循环输出1～100

【出自HW面试题】

难度系数：★★☆☆☆ 被考察系数：★★★★☆

题目描述：

实现一个函数，要求在不使用循环的前提下输出1～100。

分析与解答：

很多情况下，循环都可以使用递归来给出等价的实现，实现代码如下：

第7章 排列组合与概率

排列组合常应用于字符串或序列中，而求解排列组合的方法也比较固定：第一种是类似于动态规划的方法，即保存中间结果，依次附上新元素，产生新的中间结果；第二种是递归法，通常是在递归函数里，使用for循环，遍历所有排列或组合的可能，然后在for循环语句内调用递归函数。本章所涉及的排列组合相关问题很多都采用的是以上两种方法。

概率论是计算机科学非常重要的基础学科之一，由于概率型面试笔试题可以综合考查求职者的思维能力、应变能力以及数学能力，所以概率题也是在程序员求职过程中经常会遇到的问题。

7.1 如何求数字的组合

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

用1、2、2、3、4和5这六个数字，写一个main函数，打印出所有不同的排列，例如：512234、412345等，要求：“4”不能在第三位，“3”与“5”不能相连。

分析与解答：

打印数字的排列组合方式的最简单的方法就是递归，但本题存在两个难点：第一，数字中存在重复数字，第二，明确规定了某些位的特性。显然，采用常规的求解方法似乎不能完全适用了。

其实，可以换一种思维，把求解这6个数字的排列组合问题转换为大家都熟悉的图的遍历的问题，解答起来就容易多了。可以把1、2、2、3、4和5这6个数看成是图的6个结点，对这6个结点两两相连可以组成一个无向连通图，这6个数对应的全排列等价于从这个图中各个结点出发深度优先遍历这个图中所有可能路径所组成的数字集合。例如，从结点“1”出发所有的遍历路径组成了以“1”开头的所有数字的组合。由于“3”与“5”不能相连，因此，在构造图的时候使图中“3”和“5”对应的结点不连通就可以满足这个条件。对于“4”不能在第三位，可以在遍历结束后判断是否满足这个条件。

具体而言，实现步骤如下所示：

（1）用1、2、2、3、4和5这6个数作为6个结点，构造一个无向连通图。除了“3”与“5”不连通外，其他的所有结点都两两相连。

（2）分别从这6个结点出发对图做深度优先遍历。每次遍历完所有结点的时候，把遍历的路径对应数字的组合记录下来，如果这个数字的第三位不是“4”，则把这个数字存放到集合Set中（由于这6个数中有重复的数，因此，最终的组合肯定也会有重复的。由于集合Set的特点为集合中的元素是唯一的，不能有重复的元素，因此，通过把组合的结果放到Set中可以过滤掉重复的组合）。

（3）遍历Set集合，打印出集合中所有的结果，这些结果就是本问题的答案。实现代码如下：

由于结果过多，因此这里就不列出详细的运行结果了。

7.2 如何拿到最多金币

【出自WS笔试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

10个房间里放着数量随机的金币。每个房间只能进入一次，并只能在一个房间中拿金币。一个人采取如下策略：前4个房间只看不拿。随后的房间只要看到比前4个房间都多的金币数，就拿。否则就拿最后一个房间的金币。编程计算这种策略拿到最多金币的概率。

分析与解答：

这道题要求一个概率的问题，由于10个房间里放的金币的数量是随机的，因此，在编程实现的时候首先需要生成10个随机数来模拟10个房间里金币的数量。然后判断通过这种策略是否能拿到最多的金币。如果仅仅通过一次模拟来求拿到最多金币的概率显然是不准确的，那么就需要进行多次模拟，通过记录模拟的次数m，拿到最多金币的次数n，从而可以计算出拿到最多金币的概率n/m。显然这个概率与金币的数量以及模拟的次数有关系。模拟的次数越多越能接近真实值。下面以金币数为1～10的随机数，模拟次数为1000次为例给出实现代码：

程序的运行结果如下：

0.421

运行结果分析：

运行结果与金币个数的选择以及模拟的次数都有关系，而且由于是个随机问题，因此同样的程序每次的运行结果也会不同。

7.3 如何求正整数n所有可能的整数组合

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个正整数n，求解出所有和为n的整数组合，要求组合按照递增方式展示，而且唯一。例如：4=1+1+1+1、1+1+2、1+3、2+2、4（4+0）。

分析与解答：

以数值4为例，和为4的所有的整数组合一定都小于4（1，2，3，4）。首先选择数字1，然后用递归的方法求和为3（4-1）的组合，一直递归下去直到用递归求和为0的组合的时候，所选的数字序列就是一个和为4的数字组合。然后第二次选择2，接着用递归求和为2（4-2）的组合；同理下一次选3，然后用递归求和为1（4-3）的所有组合。依此类推，直到找出所有的组合为止，实现代码如下：

程序的运行结果如下：

运行结果分析：

从上面运行结果可以看出，满足条件的组合是：{1，1，1，1}，{1，1，2}，{1，3}，{2，2}，{4}，其他的为调试信息。从打印出的信息可以看出：在求和为4的组合中，第一步选择了1；然后求3（4-1）的组合也选了1，求2（3-1）的组合的第一步也选择了1，依次类推，找出第一个组合为{1，1，1，1}。然后通过count--和i++找出最后两个数字1与1的另外一种组合2，最后三个数字的另外一种组合3；接下来用同样的方法分别选择2、3作为组合的第一个数字，就可以得到以上结果。

代码i=（count==0？1：result[count-1]）；用来保证：组合中的下一个数字一定不会小于前一个数字，从而保证了组合的递增性。如果不要求递增（例如把{1，1，2}和{2，1，1}看作两种组合），那么把上面一行代码改成i=1即可。

7.4 如何用一个随机函数得到另外一个随机函数

【出自XM面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

有一个函数fun能返回0和1两个值，返回0和1的概率都是1/2，问怎么利用这个函数得到另一个函数fun2，使fun2也只能返回0和1，且返回0的概率为1/4，返回1的概率为3/4。

分析与解答：

func1得到1与0的概率都为1/2。因此，可以调用两次func1，分别生成两个值a1与a2，用这两个数组成一个二进制a2a1，它的取值的可能性为00，01，10，11，并且得到每个值的概率都为（1/2）*（1/2）=1/4，因此，如果得到的结果为00，则返回0（概率为1/4），其他情况返回1（概率为3/4）。实现代码如下：

程序的运行结果如下：

1 1 1 0 1 1 0 1 1 0 1 1 1 1 0 1

1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 0

由于结果是随机的，调用的次数越大，返回的结果就越接近1/4与3/4。

7.5 如何等概率地从大小为n的数组中选取m个整数

【出自ALBB面试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

随机地从大小为n的数组中选取m个整数，要求每个元素被选中的概率相等。

分析与解答：

从n个数中随机选出一个数的概率为1/n，然后在剩下的n-1个数中再随机找出一个数的概率也为1/n（第一次没选中这个数的概率为（n-1）/n，第二次选中这个数的概率为1/（n-1），因此，随机选出第二个数的概率为（（n-1）/n）*（1/（n-1））=1/n），依次类推，在剩下的k个数中随机选出一个元素的概率都为1/n。因此，这种方法的思路是：首先从有n个元素的数组中随机选出一个元素，然后把这个选中的数字与数组第一个元素交换，接着从数组后面的n-1个数字中随机选出1个数字与数组第二个元素交换，依次类推，直到选出m个数字为止，数组前m个数字就是随机选出来的m个数字，且它们被选中的概率相等。实现代码如下：

程序的运行结果如下：

1 8 9 7 2 4

算法性能分析：

这种方法的时间复杂度为O（m）。

7.6 如何组合1、2和5这三个数使其和为100

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

求出用1、2和5这三个数不同个数组合的和为100的组合个数。为了更好地理解题目的意思，下面给出几组可能的组合：100个1、0个2和0个5，它们的和为100；50个1、25个2和0个5的和也是100；50个1、20个2和2个5的和也为100。

分析与解答：

方法一：蛮力法

最简单的方法就是对所有的组合进行尝试，然后判断组合的结果是否满足和为100，这些组合有如下限制：1的个数最多为100个，2的个数最多为50个，5的个数最多为20个。实现思路是：遍历所有可能的组合1的个数x（0＜=x＜=100），2的个数y（0=＜y＜=50），5的个数z（0＜=z＜=20），判断x+2y+5z是否等于100，如果相等，则满足条件，实现代码如下：

程序的运行结果如下：

541

算法性能分析：

这种方法循环的次数为101*51*21。

方法二：数字规律法

针对这种数学公式的运算，一般都可以通过找出运算的规律进而简化运算的过程，对于本题而言，对x+2y+5z=100进行变换可以得到x+5z=100-2y。从这个表达式可以看出，x+5z是偶数且x+5z＜=100。因此，求满足x+2y+5z=100组合的个数就可以转换为求满足“x+5z是偶数且x+5z＜=100”的个数。可以通过对z的所有可能的取值（0＜=z＜=20）进行遍历从而计算满足条件的x的值。

当z=0时，x的取值为0，2，4，，100（100以内所有的偶数），个数为（100+2）/2

当z=1时，x的取值为1，3，5，，95（95以内所有的奇数），个数为（95+2）/2

当z=2时，x的取值为0，2，4，，90（90以内所有的偶数），个数为（90+2）/2

当z=3时，x的取值为1，3，5，，85（85以内所有的奇数），个数为（85+2）/2

……

当z=19时，x的取值为5，3，1（5以内所有的奇数），个数为（5+2）/2

当z=20时，x的取值为0（0以内所有的偶数），个数为（0+2）/2

根据这个思路，实现代码如下：

算法性能分析：

这种方法循环的次数为21。

7.7 如何判断有几盏灯泡还亮着

【出自HW面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

100个灯泡排成一排，第一轮将所有灯泡打开；第二轮每隔一个灯泡关掉一个，即排在偶数的灯泡被关掉；第三轮每隔两个灯泡，将开着的灯泡关掉，关掉的灯泡打开。依次类推，第100轮结束的时候，有几盏灯泡还亮着？

分析与解答：

（1）对于每盏灯，当拉动的次数是奇数时，灯就是亮着的，当拉动的次数是偶数时，灯就是关着的。

（2）每盏灯拉动的次数与它的编号所含约数的个数有关，它的编号有几个约数，这盏灯就被拉动几次。

（3）1～100这100个数中有哪几个数，约数的个数是奇数？

我们知道，一个数的约数都是成对出现的，只有完全平方数约数的个数才是奇数个。

所以，这100盏灯中有10盏灯是亮着的，它们的编号分别是：1、4、9、16、25、36、49、64、81和100。

下面是程序的实现：

程序的运行结果如下：

亮着的灯的编号是：1

亮着的灯的编号是：4

亮着的灯的编号是：9

亮着的灯的编号是：16

亮着的灯的编号是：25

亮着的灯的编号是：36

亮着的灯的编号是：49

亮着的灯的编号是：64

亮着的灯的编号是：81

亮着的灯的编号是：100

最后总共有10盏灯亮着。

第8章 排序

排序问题一直是计算机技术研究的重要问题，排序算法的好坏直接影响程序的执行速度和辅助存储空间的占有量，所以各大IT企业在笔试面试中也经常出现有关排序的题目。本节将详细分析各种常见的排序算法，并从时间复杂度、空间复杂度和适用情况等多个方面对它们进行综合比较。

8.1 如何进行选择排序

【出自HW面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用选择排序对数组进行升序排列。

分析与解答：

选择排序是一种简单直观的排序算法，它的基本原理如下：对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将该记录与第一个记录进行交换；接着对不包括第一个记录以外的其他记录进行第二轮比较，得到最小的记录并与第二个记录进行位置交换；重复该过程，直到进行比较的记录只有一个时为止。以数组{38，65，97，76，13，27，49}为例（假设要求为升序排列），具体步骤如下：

第一趟排序后：13[65 97 76 38 27 49]

第二趟排序后：13 27[97 76 38 65 49]

第三趟排序后：13 27 38[76 97 65 49]

第四趟排序后：13 27 38 49[97 65 76]

第五趟排序后：13 27 38 49 65[97 76]

第六趟排序后：13 27 38 49 65 76[97]

最后排序结果：13 27 38 49 65 76 97

程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

算法性能分析：

选择排序是一种不稳定的排序方法，最好、最坏和平均情况下的时间复杂度都为O（n^2），空间复杂度为O（1）。

8.2 如何进行插入排序

【出自TX面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用插入排序对数组进行升序排列。

分析与解答：

对于给定的一组记录，初始时假设第一个记录自成一个有序序列，其余的记录为无序序列；接着从第二个记录开始，按照记录的大小依次将当前处理的记录插入到其之前的有序序列中，直至最后一个记录插入到有序序列中为止。以数组{38，65，97，76，13，27，49}为例（假设要求为升序排列），直接插入排序具体步骤如下：

第一步插入38以后：[38]65 97 76 13 27 49

第二步插入65以后：[38 65]97 76 13 27 49

第三步插入97以后：[38 65 97]76 13 27 49

第四步插入76以后：[38 65 76 97]13 27 49

第五步插入13以后：[13 38 65 76 97]27 49

第六步插入27以后：[13 27 38 65 76 97]49

第七步插入49以后：[13 27 38 49 65 76 97]

代码示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

算法性能分析：

插入排序是一种稳定的排序方法，最好情况下的时间复杂度为O（n），最坏情况下的时间复杂度为O（n^2），平均情况下的时间复杂度为O（n^2）。空间复杂度为O（1）。

8.3 如何进行冒泡排序

【出自HW面试题】

难度系数：★★★☆☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用选择排序对数组进行升序排列。

分析与解答：

冒泡排序顾名思义就是整个过程就像气泡一样往上升，单向冒泡排序的基本思想是（假设由小到大排序）：对于给定的n个记录，从第一个记录开始依次对相邻的两个记录进行比较，当前面的记录大于后面的记录时，交换其位置，进行一轮比较和换位后，n个记录中的最大记录将位于第n位；然后对前（n-1）个记录进行第二轮比较；重复该过程直到进行比较的记录只剩下一个时为止。

以数组{36，25，48，12，25，65，43，57}为例（假设要求为升序排列），具体排序过程如下：

初始状态：[36 25 48 12 25 65 43 57]

1趟排序：[25 36 12 25 48 43 57 65]

2趟排序：[25 12 25 36 43 48]57 65

3趟排序：[12 25 25 36 43]48 57 65

4趟排序：[12 25 25 36]43 48 57 65

5趟排序：[12 25 25]36 43 48 57 65

6趟排序：[12 25]25 36 43 48 57 65

7趟排序：[12]25 25 36 43 48 57 65

程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

冒泡排序是一种稳定的排序方法，最好情况下的时间复杂度为O（n），最坏情况下时间复杂度为O（n^2），平均情况下的时间复杂度为O（n^2）。空间复杂度为O（1）。

引申：如何进行双向冒泡排序

答案：双向冒泡排序是冒泡排序的一种优化，它的基本思想是首先将第一个记录的关键字和第二个记录的关键字进行比较，若为“逆序”（即L.r[1].key＞L.r[2].key），则将两个记录交换，然后比较第二个记录和第三个记录的关键字。依次类推，直至第n-1个记录的关键字和第n个记录的关键字比较过为止。这是第一趟冒泡排序，其结果是使得关键字最大的记录被安置到最后一个记录的位置上。

第一趟排序之后进行第二趟冒泡排序，将第n-2个记录的关键字和第n-1个记录的关键字进行比较，若为“逆序”（即L.r[n-1].key＜L.r[n-2].key），则将两个记录交换，然后比较第n-3个记录和n-2个记录的关键字。依次类推，直至第1个记录的关键字和第2个记录的关键字比较过为止。其结果是使得关键字最小的记录被安置到第一个位置上。

再对其余的n-2个记录进行上述同样的操作，其结果是使关键字次大的记录被安置到第n-1个记录的位置，使关键字次小的记录被安置到第2个记录的位置。

通常，第i趟冒泡排序是：若i为奇数，则从L.r[i/2+1]～L.r[n-i/2]依次比较相邻两个记录的关键字，并在“逆序”时交换相邻记录，其结果是这n-i+1个记录中关键字最大的记录被交换到第n-i/2的位置上；若i为偶数，则从L.r[n-i/2]～L.r[i/2]依次比较相邻两个记录的关键字，并在“逆序”时交换相邻记录，其结果是这n-i+1个记录中关键字最小的记录被交换到第i/2的位置上。整个排序过程需要进行K（1≤K＜n）趟冒泡排序，同样判别冒泡排序结束的条件仍然是“在一趟排序过程中没有进行过交换记录的操作”。

程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

算法性能分析：

双向冒泡排序跟普通冒泡排序的时间复杂度相同。但是，双向冒泡排序能解决普通冒泡排序的乌龟问题。乌龟问题是指假设需要将序列按照升序序列排序，序列中的较小的数字又大量存在于序列的尾部，这样会让小数字向前移动得很缓慢。

8.4 如何进行归并排序

【出自JD笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用归并排序对数组进行升序排列。

分析与解答：

归并排序是利用递归与分治技术将数据序列划分成为越来越小的半子表，再对半子表排序，最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列。其中“归”代表的是递归的意思，即递归地将数组折半地分离为单个数组。例如，数组[2，6，1，0]会先折半，分为[2，6]和[1，0]两个子数组，然后再折半将数组分离分为[2]，[6]和[1]，[0]。“并”就是将分开的数据按照从小到大或者从大到小的顺序再放到一个数组中。如上面的[2]、[6]合并到一个数组中是[2，6]，[1]、[0]合并到一个数组中是[0，1]，然后再将[2，6]和[0，1]合并到一个数组中即为[0，1，2，6]。

具体而言，归并排序算法的原理如下：对于给定的一组记录（假设共有n个记录），首先将每两个相邻的长度为1的子序列进行归并，得到n/2（向上取整）个长度为2或1的有序子序列，再将其两两归并，反复执行此过程，直到得到一个有序序列为止。

所以，归并排序的关键就是两步：第一步，划分子表；第二步，合并半子表。以数组{49，38，65，97，76，13，27}为例（假设要求为升序排列），排序过程如下：

程序示例如下：

程序的输出结果如下：

9 8 7 6 5 4 3 2 1 0

二路归并排序的过程需要进行log2ⁿ趟。每一趟归并排序的操作，就是将两个有序子序列进行归并，而每一对有序子序列归并时，记录的比较次数均小于等于记录的移动次数，记录移动的次数均等于文件中记录的个数n，即每一趟归并的时间复杂度为O（n）。因此二路归并排序在最好、最坏和平均情况的时间复杂度为O（nlog2ⁿ）。而且是一种稳定的排序方法，空间复杂度为O（1）。

8.5 如何进行快速排序

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

给定一个无序整型数组，请用快速排序算法对数组进行升序排列。

分析与解答：

快速排序是一种非常高效的排序算法，它采用“分而治之”的思想，把大的拆分为小的，小的再拆分为更小的。其原理是：对于一组给定的记录，通过一趟排序后，将原序列分为两部分，其中前部分的所有记录均比后部分的所有记录小，然后再依次对前后两部分的记录进行快速排序，递归该过程，直到序列中的所有记录均有序为止。

具体算法步骤如下：

1）分解：将输入的序列array[m，…，n]划分成两个非空子序列array[m，…，k]和array[k+1，…，n]，使array[m，…，k]中任一元素的值不大于array[k+1，…，n]中任一元素的值。

2）递归求解：通过递归调用快速排序算法分别对array[m，…，k]和array[k+1，…，n]进行排序。

3）合并：由于对分解出的两个子序列的排序是就地进行的，所以在array[m，…，k]和array[k+1，…，n]都排好序后，不需要执行任何计算，array[m，…，n]就已排好序。

以数组{49，38，65，97，76，13，27，49}为例（假设要求为升序排列）。

第一趟排序过程如下：

初始化关键字[49 38 65 97 76 13 27 49]

第一次交换后：[27 38 65 97 76 13 49 49]

第二次交换后：[27 38 49 97 76 13 65 49]

j向左扫描，位置不变，第三次交换后：[27 38 13 97 76 49 65 49]

i向右扫描，位置不变，第四次交换后：[27 38 13 49 76 97 65 49]

j向左扫描[27 38 13 49 76 97 65 49]

整个排序过程如下：

初始化关键字[49 38 65 97 76 13 27 49]

一趟排序之后：[27 38 13]49[76 97 65 49]

二趟排序之后：[13]27[38]49[49 65]76[97]

三趟排序之后：13 27 38 49 49[65]76 97

最后的排序结果：13 27 38 49 49 65 76 97

程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

当初始的序列整体或局部有序时，快速排序的性能将会下降，此时快速排序将退化为冒泡排序。

算法性能分析：

（1）最坏时间复杂度

最坏情况是指每次区间划分的结果都是基准关键字的左边（或右边）序列为空，而另一边的区间中的记录项仅比排序前少了一项，即选择的基准关键字是待排序的所有记录中最小或者最大的。例如，若选取第一个记录为基准关键字，当初始序列按递增顺序排列时，每次选择的基准关键字都是所有记录中的最小者，这时记录与基准关键字的比较次数会增多。因此，在这种情况下，需要进行（n-1）次区间划分。对于第k（0＜k＜n）次区间划分，划分前的序列长度为（n-k+1），需要进行（n-k）次记录的比较。当k从1～（n-1）时，进行的比较次数总共为n（n-1）/2，所以在最坏情况下快速排序的时间复杂度为O（n²）。

（2）最好时间复杂度

最好情况是指每次区间划分的结果都是基准关键字左右两边的序列长度相等或者相差为1，即选择的基准关键字为待排序的记录中的中间值。此时，进行的比较次数总共为nlog₂ⁿ所以在最好情况下快速排序的时间复杂度为O（nlogn）。

（3）平均时间复杂度

快速排序的平均时间复杂度为O（log₂ⁿ）。虽然快速排序在最坏情况下的时间复杂度为O（n²），但是在所有平均时间复杂度为O（log₂ⁿ）的算法中，快速排序的平均性能是最好的。

（4）空间复杂度

快速排序的过程中需要一个栈空间来实现递归。当每次对区间的划分都比较均匀时（即最好情况），递归树的最大深度为logn+1（logn为向上取整）；当每次区间划分都使得有一边的序列长度为0时（即最好情况），递归树的最大深度为n。在每轮排序结束后比较基准关键字左右的记录个数，对记录多的一边先进行排序，此时，栈的最大深度可降为logn。因此，快速排序的平均空间复杂度为O（logn）。

（5）基准关键字的选取

基准关键字的选择是决定快速排序算法性能的关键。常用的基准关键字的选择有以下几种方式：

1）三者取中。三者取中是指在当前序列中，将其首、尾和中间位置上的记录进行比较，选择三者的中值作为基准关键字，在划分开始前交换序列中的第一个记录与基准关键字的位置。

2）取随机数。取left（左边）和right（右边）之间的一个随机数m（left≤m≤right），用n[m]作为基准关键字。这种方法使得n[left]～n[right]之间的记录是随机分布的，采用此方法得到的快速排序一般称为随机的快速排序。

需要注意快速排序与归并排序的区别与联系。快速排序与归并排序的原理都是基于分治思想，即首先把待排序的元素分成两组，然后分别对这两组排序，最后把两组结果合并起来。

而它们的不同点在于，进行的分组策略不同，后面的合并策略也不同。归并排序的分组策略是假设待排序的元素存放在数组中，那么其把数组前面一半元素作为一组，后面一半元素作为另外一组。而快速排序则是根据元素的值来分组，即大于某个值的元素放在一组，而小于某个值的元素放在另外一组，该值称为基准值。所以，对整个排序过程而言，基准值的挑选非常重要，如果选择不合适、太大或太小，那么所有的元素都分在一组了。对于快速排序和归并排序来说，如果分组策略越简单，则后面的合并策略就越复杂，因为快速排序在分组时，已经根据元素大小来分组了，而合并的时候，只需把两个分组合并起来就行了，归并排序则需要对两个有序的数组根据大小进行合并。

8.6 如何进行希尔排序

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★☆☆

题目描述：

给定一个无序整型数组，请用希尔排序对数组进行升序排列。

分析与解答：

希尔排序也称为“缩小增量排序”。它的基本原理是：首先将待排序的元素分成多个子序列，使得每个子序列的元素个数相对较少，对各个子序列分别进行直接插入排序，待整个待排序序列“基本有序后”，再对所有元素进行一次直接插入排序。

具体步骤如下：

1）选择一个步长序列t1，t2，…，tk，满足ti＞tj（i＜j），tk=1。

2）按步长序列个数k，对待排序序列进行k趟排序。

3）每趟排序，根据对应的步长ti，将待排序列分割成ti个子序列，分别对各个子序列进行直接插入排序。

需要注意的是，当步长因子为1时，所有元素作为一个序列来处理，其长度为n。以数组{26，53，67，48，57，13，48，32，60，50}（假设要求为升序排列），步长序列{5，3，1}为例。具体步骤如下：

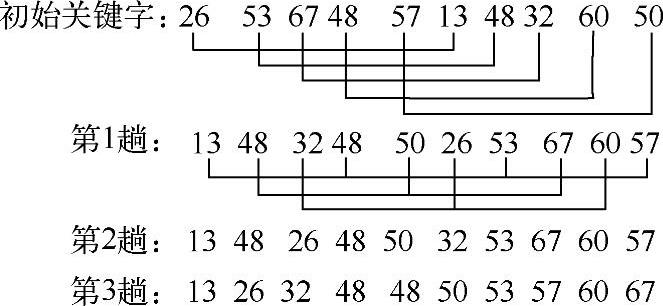
程序示例如下：

程序的输出结果如下：

0 1 2 3 4 5 6 7 8 9

算法性能分析：

希尔排序的关键并不是随便地分组后各自排序，而是将相隔某个“增量”的记录组成一个子序列，实现跳跃式的移动，使得排序的效率提高。希尔排序是一种不稳定的排序方法，平均时间复杂度为O（nlogn），最差情况下的时间复杂度为O（n^s）（1＜s＜2），空间复杂度为O（1）。

8.7 如何进行堆排序

【出自BD笔试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

给定一个无序整型数组，请用堆排序对数组进行升序排列。

分析与解答：

堆是一种特殊的树形数据结构，其每个结点都有一个值，通常提到的堆都是指一棵完全二叉树，根结点的值小于（或大于）两个子结点的值，同时根结点的两个子树也分别是一个堆。

堆排序是一树形选择排序，在排序过程中，将R[1，…，N]看成是一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系来选择最小的元素。

堆一般分为大顶堆和小顶堆两种不同的类型。对于给定n个记录的序列（r（1），r（2），…，r（n）），当且仅当满足条件（r（i）≥r（2i），i=1，2，…，n）时称之为大顶堆，此时堆顶元素必为最大值。对于给定n个记录的序列（r（1），r（2），…，r（n）），当且仅当满足条件（r（i）≤r（2i+1），i=1，2，…，n）时称之为小顶堆，此时堆顶元素必为最小值。

堆排序的思想是对于给定的n个记录，初始时把这些记录看作为一棵顺序存储的二叉树，然后将其调整为一个大顶堆，然后将堆的最后一个元素与堆顶元素（即二叉树的根结点）进行交换后，堆的最后一个元素即为最大记录；接着将前（n-1）个元素（即不包括最大记录）重新调整为一个大顶堆，再将堆顶元素与当前堆的最后一个元素进行交换后得到次大的记录，重复该过程直到调整的堆中只剩一个元素时为止，该元素即为最小记录，此时可得到一个有序序列。

堆排序主要包括两个过程：一是构建堆；二是交换堆顶元素与最后一个元素的位置。程序示例如下：

程序的输出结果如下：

27 18 14 13 1 0

算法性能分析：

堆排序方法对记录较少的文件效果一般，但对于记录较多的文件还是很有效的，其运行时间主要耗费在创建堆和反复调整堆上。堆排序即使在最坏情况下，其时间复杂度也为O（nlogn）。它是一种不稳定的排序方法。

8.8 各种排序算法有什么优劣

各种排序算法的比较如下表所示。

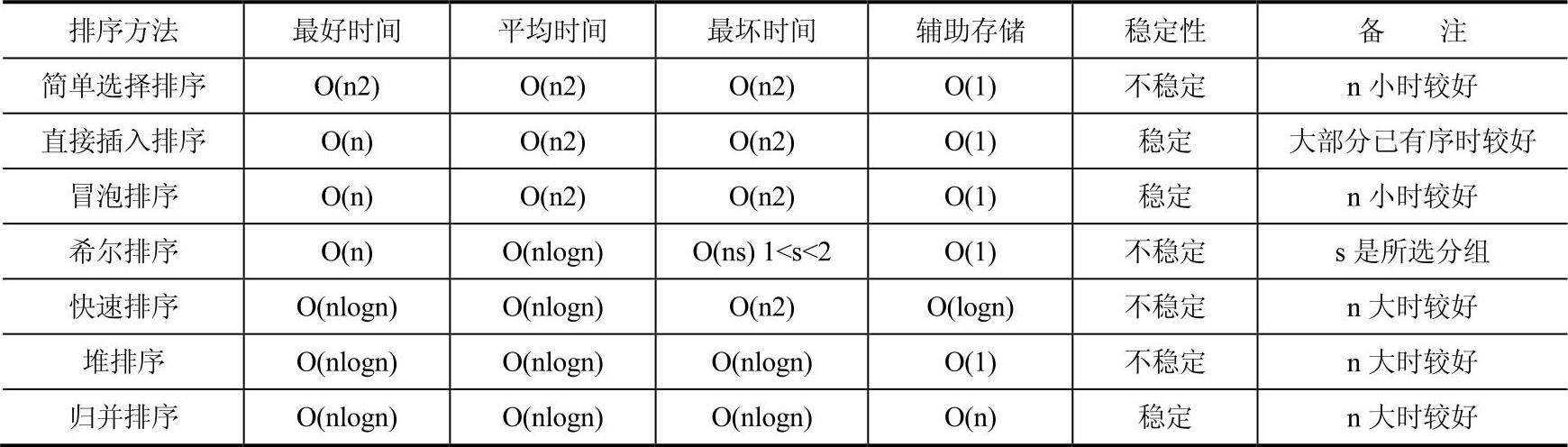
从该表中可以得到以下几个方面的结论：

1）简单地说，所有相等的数经过某种排序方法后，仍能保持它们在排序之前的相对次序，就称这种排序方法是稳定的，反之就是非稳定的。例如，一组数排序前是a1，a2，a3，a4，a5，其中a2=a4，经过某种排序后为a1，a2，a4，a3，a5，则说这种排序是稳定的，因为a2排序前在a4的前面，排序后它还是在a4的前面。假如变成a1，a4，a2，a3，a5就不是稳定的了。各种排序算法中稳定的排序算法有直接插入排序、冒泡排序和归并排序，而不稳定的排序算法有希尔排序、快速排序、简单选择排序和堆排序。

2）时间复杂度为O（n2）的排序算法有直接插入排序、冒泡排序、快速排序和简单选择排序，时间复杂性为O（nlogn）的排序算法有堆排序和归并排序。

3）空间复杂度为O（1）的算法有简单选择排序、直接插入排序、冒泡排序、希尔排序和堆排序，空间复杂杂度为O（n）的算法是归并排序，空间复杂度为O（logn）的算法是快速排序。

4）虽然直接插入排序和冒泡排序的速度比较慢，但是当初始序列整体或局部有序时，这两种排序算法会有较好的效率。当初始序列整体或局部有序时，快速排序算法的效率会下降。当排序序列较小且不要求稳定性时，直接选择排序效率较好；要求稳定性时，冒泡排序效率较好。

除了以上这几种排序算法以外，还有位图排序、桶排序及基数排序等。每种排序算法都有其最佳适用场合。例如，当待排序数据规模巨大，而对内存大小又没有限制时，位图排序则是最高效的排序算法。所以，在选择使用排序算法的时候，一定要结合实际情况进行分析。

第9章 大数据

计算机硬件的扩容确实可以极大地提高程序的处理速度，但考虑到其技术、成本等方面的因素，它并非一条放之四海而皆准的途径。而随着互联网技术的发展，特别是机器学习、深度学习、大数据、人工智能、云计算、物联网及移动通信技术的发展，每时每刻，数以亿万计的用户产生着数量巨大的信息，海量数据时代已经来临。由于通过对海量数据的挖掘能有效地揭示用户的行为模式，加深对用户需求的理解，提取用户的集体智慧，从而为研发人员决策提供依据，提升产品用户体验，进而占领市场，所以当前各大互联网公司研究都将重点放在了海量数据分析上，但是，只寄希望于硬件扩容是很难满足海量数据分析需要的，如何利用现有条件进行海量信息处理，已经成为各大互联网公司亟待解决的问题。所以，海量信息处理正日益成为当前程序员笔试面试中一个新的亮点。

不同于常规量级数据中提取信息，在海量信息中提取有用数据，会存在以下几个方面的问题：首先，数据量过大，数据中什么情况都可能存在，如果信息数量只有20条，人工可以逐条进行查找、比对，可是当数据规模扩展到上百条、数千条、数亿条，甚至更多时，仅仅通过人工已经无法解决存在的问题，必须通过工具或者程序进行处理。其次，对海量数据信息处理，还需要有良好的软硬件配置，合理使用工具，合理分配系统资源，通常情况下，如果需要处理的数据量非常大，超过了TB级，小型机、大型工作站是要考虑的，普通的计算机如果有好的方法也可以考虑，例如通过联机做成工作集群。最后，对海量数据信息处理时，要求很高的处理方法和技巧，如何进行数据挖掘算法的设计以及如何进行数据的存储访问等都是研究的难点。

针对海量数据的处理，可以使用的方法非常多，常见的方法有Hash法、Bit-map（位图）法、Bloomfilter法、数据库优化法、倒排索引法、外排序法、Trie树、堆、双层桶法以及MapReduce法等。其中，Hash法、Bit-map（位图）法、Trie树、堆等方法的考察频率最高、使用范围最为广泛，是读者需要重点掌握的方法。

9.1 如何从大量的url中找出相同的url

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

给定a、b两个文件，各存放50亿个url，每个url各占64B，内存限制是4GB，请找出a、b两个文件共同的url。

分析与解答：

由于每个url需要占64B，所以50亿个url占用空间的大小为50亿×64=5GB×64=320GB。由于内存大小只有4GB，因此不可能一次性把所有的url都加载到内存中处理。对于这个类型的题目，一般都需要使用分治法，即把一个文件中的url按照某一特征分成多个文件，使得每个文件的内容都小于4GB，这样就可以把这个文件一次性读到内存中进行处理了。对于本题而言，主要的实现思路如下：

（1）遍历文件a，对遍历到的url求hash（url）%500，根据计算结果把遍历到的url分别存储到a0，a1，a2，…，a499（计算结果为i的url存储到文件ai中），这样每个文件的大小大约为600M。当某一个文件中url的大小超过2GB的时候，可以按照类似的思路把这个文件继续分为更小的子文件（例如：如果a1大小超过2GB，那么可以把文件继续分成a11，a12…）。

（2）使用同样的方法遍历文件b，把文件b中的url分别存储到文件b0，b1，…，b499中。

（3）通过上面的划分，与ai中url相同的的url^一定在bi中。由于ai与bi中所有的url的大小不会超过4GB，因此可以把它们同时读入到内存中进行处理。具体思路：遍历文件ai，把遍历到的url存入到hash_set中，接着遍历文件bi中的url，如果这个url在hash_set中存在，那么说明这个url是这两个文件共同的url，可以把这个url保存到另外一个单独的文件中。当把文件a0～a499都遍历完成后，就找到了两个文件共同的url。

9.2 如何从大量数据中找出高频词

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

有一个1GB大小的文件，文件里面每一行是一个词，每个词的大小不超过16B，内存大小限制是1MB，要求返回频数最高的100个词。

分析与解答：

由于文件大小为1G，而内存大小只有1MB，因此不可能一次把所有的词读入到内存中处理，因此也需要采用分治的方法，把一个大的文件分解成多个小的子文件，从而保证每个文件的大小都小于1MB，进而可以直接被读取到内存中处理。具体的思路如下：

（1）遍历文件，对遍历到的每一个词，执行如下Hash操作：hash（x）%2000，将结果为i的词存放到文件ai中，通过这个分解步骤，可以使每个子文件的大小大约为400KB左右，如果这个操作后某个文件的大小超过1MB了，那么可以采用相同的方法对这个文件继续分解，直到文件的大小小于1MB为止。

（2）统计出每个文件中出现频率最高的100个词。最简单的方法为使用hash_map来实现，具体实现方法为，遍历文件中的所有词，对于遍历到的词，如果在hash_map中不存在，那么把这个词存入hash_map中（键为这个词，值为1），如果这个词在hash_map中已经存在了，那么把这个词对应的值加1。遍历完后可以非常容易地找出出现频率最高的100个词。

（3）第（2）步找出了每个文件出现频率最高的100个词，这一步可以通过维护一个小顶堆来找出所有词中出现频率最高的100个。具体方法为，遍历第一个文件，把第一个文件中出现频率最高的100个词构建成一个小顶堆。（如果第一个文件中词的个数小于100，可以继续遍历第2个文件，直到构建好有100个结点的小顶堆为止）。继续遍历，如果遍历到的词的出现次数大于堆顶上词的出现次数，可以用新遍历到的词替换堆顶的词，然后重新调整这个堆为小顶堆。当遍历完所有文件后，这个小顶堆中的词就是出现频率最高的100个词。当然这一步也可以采用类似归并排序的方法把所有文件中出现频率最高的100个词排序，最终找出出现频率最高的100个词。

引申：怎么在海量数据中找出重复次数最多的一个

前面的算法是求解top100，而这道题目只是求解top1，可以使用同样的思路来求解。唯一不同的是，在求解出每个文件中出现次数最多的数据后，接下来从各个文件中出现次数最多的数据中找出出现次数最多的数不需要使用小顶堆，只需要使用一个变量就可以完成。方法很简单，此处不再赘述。

9.3 如何找出访问百度最多的IP

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

现有海量日志数据保存在一个超级大的文件中，该文件无法直接读入内存，要求从中提取某天访问百度次数最多的那个IP。

分析与解答：

由于这道题只关心某一天访问百度最多的IP，因此可以首先对文件进行一次遍历，把这一天访问百度的IP的相关信息记录到一个单独的文件中。接下来可以用上一节介绍的方法来求解。由于求解思路是一样的，这里不再赘述。唯一需要确定的是把一个大文件分为几个小文件比较合适。以IPv4为例，由于一个IP地址占用32位，因此最多会有2^32=4G种取值情况。如果使用hash（IP）%1024值，那么把海量IP日志分别存储到1024个小文件中。这样，每个小文件最多包含4M个IP地址。如果使用2048个小文件，那么每个文件会最多包含2M个IP地址。因此，对于这类题目而言，首先需要确定可用内存的大小，然后确定数据的大小。由这两个参数就可以确定Hash函数应该怎么设置才能保证每个文件的大小都不超过内存的大小，从而可以保证每个小的文件都能被一次性加载到内存中。

9.4 如何在大量的数据中找出不重复的整数

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

在2.5亿个整数中找出不重复的整数，注意，内存不足以容纳这2.5亿个整数。

分析与解答：

由于这道题目与前面的题目类似，也是无法一次性把所有数据加载到内存中，因此也可以采用类似的方法求解。

方法一：分治法

采用Hash法，把这2.5亿个数划分到更小的文件中，从而保证每个文件的大小不超过可用的内存的大小。然后对于每个小文件而言，所有的数据可以一次性被加载到内存中，因此可以使用hash_map或hash_set来找到每个小文件中不重复的数。当处理完所有的文件后就可以找出这2.5亿个整数中所有的不重复的数。

方法二：位图法

对于整数相关的算法的求解，位图法是一种非常实用的算法。对于本题而言，如果可用的内存空间超过1GB就可以使用这种方法。具体思路是：假设整数占用4B（如果占用8B，求解思路类似，只不过需要占用更大的内存），4个字节也就是32位，可以表示的整数的个数为2^32。由于本题只查找不重复的数，而不关心具体数字出现的次数，因此可以分别使用2bit来表示各个数字的状态：用00表示这个数字没有出现过，01表示出现过1次，10表示出现了多次，11暂不使用。

根据上面的逻辑，在遍历这2.5亿个整数的时候，如果这个整数对应的位图中的位为00，那么修改成01，如果为01则修改为10，如果为10则保持原值不变。这样当所有数据遍历完成后，可以再遍历一遍位图，位图中为01的对应的数字就是没有重复的数字。

9.5 如何在大量的数据中判断一个数是否存在

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

在2.5亿个整数中判断一个数是否存在，注意，内存不足以容纳这2.5亿个整数。

分析与解答：

显然数据量太大，不可能一次性把所有的数据都加载到内存中，那么最容易想到的方法当然是分治法。

方法一：分治法

对于大数据相关的算法题，分治法是一个非常好的方法。针对这道题而言，主要的思路为：可以根据实际可用内存的情况，确定一个Hash函数，比如hash（value）%1000，通过这个Hash函数可以把这2.5亿个数字划分到1000个文件中（a1，a2，…，a1000），然后再对待查找的数字使用相同的Hash函数求出Hash值，假设计算出的Hash值为i，如果这个数存在，那么它一定在文件ai中。通过这种方法就可以把题目的问题转换为文件ai中是否存在这个数。那么在接下来的求解过程中可以选用的思路比较多，如下所示：

（1）由于划分后的文件比较小了可以直接被装载到内存中，可以把文件中所有的数字都保存到hash_set中，然后判断待查找的数字是否存在。

（2）如果这个文件中的数字占用的空间还是太大，那么可以用相同的方法把这个文件继续划分为更小的文件，然后确定待查找的数字可能存在的文件，然后在相应的文件中继续查找。

方法二：位图法

对于这类判断数字是否存在、判断数字是否重复的问题，位图法是一种非常高效的方法。这里以32位整型为例，它可以表示数字的个数为2^32。可以申请一个位图，让每个整数对应位图中的一个bit，这样2^32个数需要位图的大小为512MB。具体实现的思路是：申请一个512M大小的位图，并把所有的位都初始化为0；接着遍历所有的整数，对遍历到的数字，把相应位置上的bit设置为1。最后判断待查找的数对应的位图上的值是多少，如果是0则表示这个数字不存在，如果是1则表示这个数字存在。

9.6 如何查询最热门的查询串

【出自TX面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

搜索引擎会通过日志文件把用户每次检索使用的所有查询串都记录下来，每个查询串的长度为1～255B。

假设目前有1000万个记录（这些查询串的重复度比较高，虽然总数是1000万，但如果除去重复后，不超过300万个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门），请统计最热门的10个查询串，要求使用的内存不能超过1GB。

分析与解答：

从题目中可以发现，每个查询串最常为255B，1000万个字符串需要占用2.55GB内存，因此无法把所有的字符串全部读入到内存中处理。对于这类型的题目，分治法是一个非常实用的方法。

方法一：分治法

对字符串设置一个Hash函数，通过这个Hash函数把字符串划分到更多更小的文件中，从而保证每个小文件中的字符串都可以直接被加载到内存中处理，然后求出每个文件中出现次数最多的10个字符串；最后通过一个小顶堆统计出所有文件中出现最多的10个字符串。

从功能角度出发，这种方法是可行的，但是由于需要对文件遍历两遍，而且Hash函数也需要被调用1000万次，所以性能不是很好，针对这道题的特殊性，下面介绍另外一种性能较好的方法。

方法二：hash_map法

虽然字符串的总数比较多，但是字符串的种类不超过300万个，因此可以考虑把所有字符串出现的次数保存在一个hash_map中（键为字符串，值为字符串出现的次数）。hash_map所需要的空间为300万*（255+4）=3MB*259=777M（其中，4表示用来记录字符串出现次数的整数占用4B）。由此可见1G的内存空间是足够用的。基于以上的分析，本题的求解思路为：

（1）遍历字符串，如果字符串在hash_map中不存在，则直接存入hash_map中，键为这个字符串，值为1。如果字符串在hash_map中已经存在了，则把对应的值直接+1。这一步操作的时间复杂度为O（N），其中N为字符串的数量。

（2）在第一步的基础上找出出现频率最高的10个字符串。可以通过小顶堆的方法来完成，遍历hash_map的前10个元素，并根据字符串出现的次数构建一个小顶堆，然后接着遍历hash_map，只要遍历到的字符串的出现次数大于堆顶字符串的出现次数，就用遍历的字符串替换堆顶的字符串，然后把堆调整为小顶堆。

（3）对所有剩余的字符串都遍历一遍，遍历完成后堆中的10个字符串就是出现次数最多的字符串。这一步的时间复杂度为O（Nlog10）。

方法三：trie树法

方法二中使用hash_map来统计每个字符串出现的次数。当这些字符串有大量相同前缀的时候，可以考虑使用trie树来统计字符串出现的次数。可以在树的结点中保存字符串出现的次数，0表示没有出现。具体的实现方法是：在遍历的时候，在trie树中查找，如果找到，则把结点中保存的字符串出现的次数加1，否则为这个字符串构建新的结点，构建完成后把叶子结点中字符串的出现次数设置为1。这样遍历完字符串后就可以知道每个字符串的出现次数，然后通过遍历这个树就可以找出出现次数最多的字符串。

trie树经常被用来统计字符串的出现次数。它的另外一个大的用途就是字符串查找，判断是否有重复的字符串等。

9.7 如何统计不同电话号码的个数

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。

分析与解答：

这个题目从本质上而言也是求解数据重复的问题，对于这类问题一般而言，首先会考虑位图法。对于本题而言，8位电话号码可以表示的范围为：00000000～99999999，如果用1bit表示一个号码，总共需要1亿个bit，总共需要大约100MB的内存。

通过上面的分析可知，这道题的主要思路是：申请一个位图并初始化为0，然后遍历所有电话号码，把遍历到的电话号码对应的位图中的bit设置为1。当遍历完成后，如果bit值为1则表示这个电话号码在文件中存在，否则这个bit对应的电话号码在文件中不存在。所以bit值为1的数量即为不同电话号码的个数。

那么对于这道题而言，最核心的算法是如何确定电话号码对应的是位图中的哪一位。下面重点介绍这个转化的方法，这里使用下面的对应方法。

00000000对应位图最后一位：0x0000…000001。

00000001对应位图倒数第二位：0x0000…0000010（1向左移1位）。

00000002对应位图倒数第三位：0x0000…0000100（1向左移2位）。

00000012对应位图的倒数十三为：0x0000…0001 0000 0000 0000。

通常，位图都是通过一个整数数组来实现的（这里假设一个整数占用4B）。由此可以得出通过电话号码获取位图中对应位置的方法为（假设电话号码为P）：

（1）通过P/32就可以计算出该电话号码在bitmap数组的下标。（因为每个整数占用32bit，通过这个公式就可以确定这个电话号码需要移动多少个32位，也就是可以确定它对应的bit在数组中的位置。）

（2）通过P%32就可以计算出这个电话号码在这个整型数字中具体的位的位置，也就是1这个数字对应的左移次数。因此可以通过把1向左移P%32位然后把得到的值与这个数组中的值做或运算，这样就可以把这个电话号码在位图中对应的为设置为1。

这个转换的操作可以通过一个非常简单的函数来实现：

9.8 如何从5亿个数中找出中位数

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★☆

题目描述：

从5亿个数中找出中位数。数据排序后，位置在最中间的数值就是中位数。当样本数为奇数时，中位数=（N+1）/2；当样本数为偶数时，中位数为N/2与1+N/2的均值（那么10G个数的中位数，就是第5G大的数与第5G+1大的数的平均值了）。

分析与解答：

如果这道题目没有内存大小的限制，可以把所有的数字排序后找出中位数，但是最好的排序算法的时间复杂度都是O（NlogN）（N为数字的个数）。这里介绍另外一种求解中位数的算法：双堆法。

方法一：双堆法

这种方法的主要思路是维护两个堆，一个大顶堆，一个小顶堆，且这两个堆需要满足如下两个特性：

特性一：大顶堆中最大的数值小于等于小顶堆中最小的数。

特性二：保证这两个堆中的元素个数的差不能超过1。

当数据总数为偶数的时候，当这两个堆建立好以后，中位数显然就是两个堆顶元素的平均值。当数据总数为奇数的时候，根据两个堆的大小，中位数一定在数据多的堆的堆顶。对于本题而言，具体实现思路：维护两个堆maxHeap与minHeap，这两个堆的大小分别为max_size和min_size。然后开始遍历数字。对于遍历到的数字data：

（1）如果data＜maxHeap的堆顶元素，此时为了满足特性1，只能把data插入到maxHeap中。为了满足特性二，需要分以下几种情况讨论。

a）如果max_size＜=min_size，说明大顶堆元素个数小于小顶堆元素个数，此时把data直接插入大顶堆中，并把这个堆调整为大顶堆。

b）如果max_size＞min_size，为了保持两个堆元素个数的差不超过1，此时需要把maxHeap堆顶的元素移动到minHeap中，接着把data插入到maxHeap中。同时通过对堆的调整分别让两个堆保持大顶堆与小顶堆的特性。

（2）如果maxHeap堆顶元素＜=data＜=minHeap堆顶元素，为了满足特性一，此时可以把data插入任意一个堆中，为了满足特性二，需要分以下几种情况讨论：

a）如果max_size＜min_size，显然需要把data插入到maxHeap中。

b）如果max_size＞min_size，显然需要把data插入到minHeap中。

c）如果max_size==min_size，可以把data插入到任意一个堆中。

（3）如果data＞maxHeap的堆顶元素，此时为了满足特性一，只能把data插入到minHeap中。为了满足特性二，需要分以下几种情况讨论。

a）如果max_size＞=min_size，那么把data插入到minHeap中。

b）如果max_size＜min_size，那么需要把minHeap堆顶元素移到maxHeap中，然后把data插入到minHeap中。

通过上述方法可以把5亿个数构建两个堆，两个堆顶元素的平均值就是中位数。

这种方法由于需要把所有的数据都加载到内存中，当数据量很大的时候，由于无法把数据一次性加载到内存中，因此这种方法比较适用于数据量小的情况。对于本题而言，5亿个数字，每个数字在内存中占4B，5亿个数字需要的内存空间为2GB内存。如果可用的内存不足2G的时候显然不能使用这种方法，因此下面介绍另外一种方法。

方法二：分治法

分治法的核心思想为把一个大的问题逐渐转换为规模较小的问题来求解。对于本题而言，顺序读取这5亿个数字；

（1）对于读取到的数字num，如果它对应的二进制中最高位为1则把这个数字写入到f1中，如果最高位是0则写入到f0中。通过这一步就可以把这5亿个数字划分成两部分，而且f0中的数字都大于f1中的数字（因为最高位是符号位）。

（2）通过上面的划分可以非常容易地知道中位数是在f0中还是在f1中，假设f1中有1亿个数，那么中位数一定在文件f0中从小到大是第1.5亿个数与它后面的一个数求平均值。

（3）对于f0可以用次高位的二进制的值继续把这个文件一分为二，使用同样的思路可以确定中位数是哪个文件中的第几个数。直到划分后的文件可以被加载到内存的时候，把数据加载到内存中后排序，从而找出中位数。

需要注意的是，这里有一种特殊情况需要考虑，当数据总数为偶数的时候，如果把文件一分为二后，发现两个文件中的数据有相同的个数，那么中位数就是数据总数小的文件中的最大值与数据总数大的文件中的最小值的平均值。对于求一个文件中所有数据的最大值或最小值，可以使用前面介绍的分治法进行求解。

9.9 如何按照query的频度排序

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

有10个文件，每个文件1GB，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求按照query的频度排序。

分析与解答：

对于这种题，如果query的重复度比较大，那么可以考虑一次性把所有query读入到内存中处理，如果query的重复率不高，那么可用的内存不足以容纳所有的query，那么就需要使用分治法或者其他的方法来解决。

方法一：hash_map法

如果query的重复率比较高，说明不同的query总数比较小，可以考虑把所有的query都加载到内存中的hash_map中（由于hash_map中针对每个不同的query只保存一个键值对，因此这些query占用的空间会远小于10GB，有希望把它们一次性都加载到内存中）。接着就可以对hash_map按照query出现的次数进行排序。

方法二：分治法

这种方法需要根据数据量的大小以及可用内存的大小来确定问题划分的规模。对于本题而言，可以顺序遍历10个文件中的query，通过Hash函数hash（query）%10把这些query划分到10个文件中，通过这样的划分，每个文件的大小为1GB左右，当然可以根据实际情况来调整hash函数，如果可用内存很小，可以把这些query划分到更多的小的文件中。

如果划分后的文件还是比较大，可以使用相同的方法继续划分，直到每个文件都可以被读取到内存中进行处理为止，然后对每个划分后的小文件使用hash_map统计每个query出现的次数，然后根据出现次数排序，并把排序好的query以及出现次数写入到另外一个单独的文件中。这样针对每个文件，都可以得到一个按照query出现次数排序的文件。

接着对所有的文件按照query的出现次数进行排序，这里可以使用归并排序（由于无法把所有的query都读入到内存中，因此这里需要使用外排序）。

9.10 如何找出排名前500的数

【出自BD面试题】

难度系数：★★★★☆ 被考察系数：★★★★★

题目描述：

有20个数组，每个数组有500个元素，并且是有序排列好的，现在如何在这20*500个数中找出排名前500的数？

分析与解答：

对于求topk的问题，最常用的方法为堆排序方法。对于本题而言，假设数组降序排列，可以采用如下方法：

1）首先建立大顶堆，堆的大小为数组的个数，即20，把每个数组最大的值（数组第一个值）存放到堆中。

2）接着删除堆顶元素，保存到另外一个大小为500的数组中，然后向大顶堆插入删除的元素所在数组的下一个元素。

3）重复步骤（1）、（2），直到删除个数为最大的k个数，这里为500。

为了在堆中取出一个数据后，能知道它是从哪个数组中取出的，从而可以从这个数组中取下一个值，可以把数组的指针存放到堆中，对这个指针提供比较大小的方法（比较指针指向的值）。为了便于理解，把题目进行简化：3个数组，每个数组有5个元素且有序，找出排名前5的数。

程序的运行结果如下：

30 29 25 20 19

通过把ROWS改成20，COLS改成50，并构造相应的数组，就能实现题目的要求。对于升序排列的数组，实现方式类似，只不过是从数组的最后一个元素开始遍历。

孙伟

程序员，目前从事面向海外市场的应用开发。有多年的Symbian和Android开发经验，对C++和Java、JVM有比较深入的了解。从Kotlin发布支持就开始将其用于实际开发，目前已经使用Kotlin完成了多个项目。

你是一名程序猿/媛吗？

你还在为找不到对象而苦恼吗？

你还在被家人催促得烦不可奈吗？

你还在整日面对电脑忙于事业无心婚恋吗？

约猿吧，程序猿/媛可以信赖的脱单家园。

在这里，你可以认识各类靠谱的婚恋对象。

在这里，你可以学习各种恋爱技巧与经验。

在这里，你可以获得情感专家一对一的解惑。

请扫描二维码加入我们：约猿吧