4.17  如何寻找最多的覆盖点

4.17 如何寻找最多的覆盖点

【出自BD笔试题】

难度系数：★★★☆☆ 被考察系数：★★★★☆

题目描述：

坐标轴上从左到右依次的点为a[0]、a[1]、a[2]…a[n-1]，设一根木棒的长度为L，求L最多能覆盖坐标轴的几个点？

分析与解答：

本题求满足a[j]-a[i]＜=L&&a[j+1]-a[i]＞L这两个条件的j与i中间的所有点个数中的最大值，即j-i+1最大，这样题目就简单多了，方法也很简单：直接从左到右扫描，使用两个索引i和j，i从位置0开始，j从位置1开始，如果a[j]-a[i]＜=L，则j++前进，并记录中间经过的点的个数，如果a[j]-a[i]＞L，则j--回退，覆盖点个数-1，回到刚好满足条件的时候，将满足条件的最大值与前面找出的最大值比较，记录下当前的最大值，然后执行i++、j++，直到求出最大的点个数。

有两点需要注意，如下所示：

（1）这里可能不存在i和j使得a[j]-a[i]刚好等于L的情况发生，所以，判断条件不能为a[j]-a[i]==L。

（2）可能存在不同的覆盖点但覆盖的长度相同的情况发生，此时只选取第一次覆盖的点。

实现代码如下：

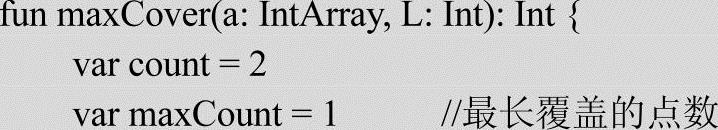
程序的运行结果如下：

覆盖的坐标点：7 8 10 11 12 13 15

最长覆盖点数：7

算法性能分析：

这种方法的时间复杂度为O（N），其中，N为数组的长度。