(二)模型选择
1.空间差异分析模型
已有文献对于城市创新能力的区域差异分析的方法有:标准差、变异系数(CV)、基尼系数、锡尔系数、洛伦兹曲线、相对发展率等。通过对这些方法的比较与分析,最终选定基尼系数、锡尔系数和相对发展指数三个指标对长江经济带科技创新能力的区域差异进行测度研究。
(1)基尼系数
基尼系数是反映地区差异的重要指标,运用基尼系数反映长江经济带城市科技创新能力在空间上的集中趋势,区位基尼系数的取值范围为[0,1],系数越大表明测度对象的空间集中趋势就越显著,其公式为:
其中n为要素总和,x-为长江经济带城市科技创新能力平均值,i,j为区域i和区域j。
(2)锡尔系数
锡尔系数可以反映出测度对象区域内和区域间的差异,运用锡尔指数对长江经济带108个城市科技创新能力的区域差异进行具体的分析。其公式为:
其中,N为城市总数;yi为i地区的发明专利申请量占整个长江经济带发明专利申请量的份额;pi为i地区的人口数占整个长江经济带总人口数的份额。计算得到的锡尔系数越大,表明各个区域之间的科技创新能力的差异越大;反之,表明各个区域之间的科技创新能力差异越小。
通过分解的锡尔系数可以反映长江经济带11个省市间的科技创新能力差异以及省市内各市之间的差异。其公式为:
其中,TBR为11省市间的差异,TWR为11省市内各城市间的差异,j代表省市内部的市级行政区。
(3)相对发展率
相对发展率(Nich)是测度相对增长量的指标,该指标能够反映各地区在一定时间段内各区域科技创新能力的变化与该时期内整个研究区域的科技创新能力变化之间的关系。其公式为:
其中,与y2i、y1i分别表示城市i在时间2和时间1的科技创新能力;y1和y2分别表示整个长江经济带在时间2和时间1的科技创新能力。相对发展指数的数值大于1,则表明考察期内该城市的科技创新能力的增长速度快于整个长江经济带的科技创新能力的平均水平。反之,如果相对发展指数的值小于1,则表明考察期内该城市的科技创新能力的增长速度慢于整个长江经济带的科技创新能力的平均水平。
2.空间相关性分析模型
运用探索性空间数据分析对长江经济带城市科技创新能力的空间相关性进行分析。探索性空间数据分析法主要运用于探索空间数据间的空间关联性,空间数据的关联性分为空间分布的非随机性和自相关性,其中空间自相关的探索是对空间数据进行分析和认识的基础。
(1)全局空间自相关分析
全局空间自相关一般采用Moran's I来测度,可以测度空间数据在整体中的空间分布特征。其计算公式为:
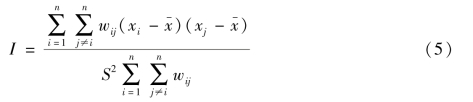
其中,
分别是区域i和区域j的属性;wij是空间权重,体现各空间区域间的联系。采用标准化统计量Z来检验空间自相关的显著性水平,其公式为:
Moran's I的取值范围为[-1,1],若Moran's I显著为正,说明区域内空间正相关,空间存在显著聚集;若Moran's I显著为负,说明区域内空间负相关;若Moran's I等于0,说明区域内不存在空间相关性。
(2)局部空间自相关分析
局部空间自相关一般采用Moran散点图和局部Moran's I指数或称LISA,可以测度空间数据在局部地区中的空间分布特征。
Moran散点图运用散点图的形式,展示变量Z与其空间滞后向量Wz(即此观测值附近相邻变量的加权平均)两者之间的相互关系。Moran散点图的横轴为观测变量,纵轴为空间滞后向量。该图共有四个象限,可以用来识别一个地区与其相邻地区的空间相关性。第一象限(HH)中的点代表科技创新能力高的城市被创新能力高的城市所包围;第二象限(HL)中的点代表科技创新能力低的城市被科技创新能力高的城市所包围;第三象限(LH)中的点代表科技创新能力高的城市被科技创新能力低的城市所包围;第四象限中的点(LL)代表科技创新能力低的城市被科技创新能力低的城市所包围。其中一、三象限代表城市科技创新能力存在空间正相关,即相似观测值之间的空间关系,而二、四象限代表城市科技创新能力存在空间负相关,即不同观测值之间的空间关系;若观测值均匀地分布在这四个象限中,那么说明观测城市之间不存在空间自相关。
将Moran散点图与LISA两者相组合,则得到Moran显著性地图即LISA集聚图,相较于Moran散点图,LISA集聚图只显示局部Moran's I显著的城市,且会标明这些城市的局部相关类型。Moran's I指数能够测度一个城市与该城市周围城市的科技创新能力在空间维度上的差别程度及其显著性。其计算公式为:
存在四种空间关联类型:高高集聚(HH)、低低集聚(DD)、高低集聚(HD)和低高集聚(DH),其含义与Moran散点图中象限的解释相同。
3.影响因素分析模型
运用空间面板模型对长江经济带城市科技创新能力的影响因素进行回归。存在两种可以用于检测空间相关性的回归模型:空间滞后模型和空间误差模型。其中空间滞后模型需要在模型解释变量中加入新的解释变量,也就是空间滞后变量,继而运用空间自相关系数来对空间相关的方向以及大小进行分析;空间误差模型则是并不改变解释变量,而在误差项中分析空间相关性,运用构造带有误差项的空间自回归结构模型,测度空间自相关系。
(1)空间滞后模型(SLM)
在空间滞后模型中,在模型的等式右边考虑空间相关,即在模型中引入空间滞后因子WY作为解释变量。公式(8)为Talen和Anselin[63]构造的包含其他解释变量的混合空间自回归模型表达式:
其中,Y为N*1维因变量向量,X为包含K个解释变量的N*1维向量,WY为前述的空间滞后因子,ε为N*1维误差向量;W为N*N维空间权重矩阵,β为解释变量系数,α为空间自相关系数。
(2)空间误差模型(SEM)
在空间误差模型中,空间相关的存在不影响回归模型的结构,模型表达式为:
其中,λ为空间自相关系数;ξ为回归误差模型的误差项。