2.1 密码学的基本概念
密码学(Cryptography)来源于希腊语Kryptós(隐藏的、秘密的)和Gráphein(书写),是指在被称为敌手的第三方存在的情况下对安全通信技术的实践和研究。早期的密码学研究如何秘密地传送消息,而现在的密码学从最基本的消息机密性研究延伸到消息完整性检测、发送方/接收方身份认证、数字签名以及访问控制等信息安全的诸多领域,是信息安全的基础与核心。
密码学可以分为密码编码学和密码分析学两个分支。其中密码编码学是研究对信息进行编码以实现隐蔽信息的学问,而密码分析学是关于如何破译密码或密码系统的研究,两者相互对立又相互促进。
密码体制有两种:对称密码体制(又称为单钥密码体制)和非对称密码体制(又称为双钥密码体制或公钥密码体制)。对称密码体制使用相同的密钥(秘密密钥)对消息进行加密/解密,系统的保密性主要由密钥的安全性决定,而与算法是否保密无关。对称密码体制设计和实现的中心课题是:用何种方法产生满足保密要求的密钥以及用何种方法将密钥安全又可靠地分配给通信双方。对称密码体制可以通过分组密码或流密码来实现,它既可以用于数据加密,又可以用于消息认证。非对称密码体制使用公钥来加密消息,使用私钥来解密。使用非对称密码体制可增强通信的安全性。
1.密码学的发展历程
密码学到目前为止经历了3个发展阶段:古典密码学、近代密码学、现代密码学。
(1)古典密码学
古典密码学是密码学发展的基础与起源。自古以来,人们就非常重视密码技术的应用,其历史可以追溯到两千多年前的凯撒大帝时期。很长一段时期内,“密码”被视为高智商人玩的游戏。所谓“密码”,是相对于“明码”来讲的,那些一目了然的、具有实际意义的消息被称为“明码”或“明文”,将这些明文消息进行特定的变换就得到对应的“密码”或“密文”。通常,密文都是看似杂乱无章的消息,只有拥有密钥的接收方才能将其恢复成明文。传统的加密方法是建立明文消息空间和密文消息空间的一一映射。比如历史上第一个密码技术——凯撒密码,还有后面的掩格密码等。这些密码虽然大都比较简单,但对于今天的密码学发展仍然具有参考价值。
(2)近代密码学
近代密码学开始于通信的机械化与电气化时期,它为密码的加密技术提供了前提,也为破译者提供了有力的武器。电子信息时代的到来给密码设计者带来前所未有的自由,他们可以利用电子计算机设计出更为复杂、保密的密码系统。
(3)现代密码学
古典密码学和近代密码学都是现代人赋予的定义,与其有关的研究算不上真正意义上的一门科学。1949年,香农发表了一篇名为《保密系统的通信理论》的著名论文,该文将信息论引入密码,奠定了密码学的理论基础,开启了现代密码学时代。
由于历史的局限,20世纪70年代中期以前的密码学研究基本上是秘密进行的,主要应用于军事和政府部门。密码学真正的蓬勃发展和广泛应用是从70年代中期开始的。1977年,美国国家标准局将数据加密标准(DES)用于非国家保密机关,该标准完全公开了加密、解密算法;此举突破了早期密码学信息保密的单一目的,使密码学得以在商业等民用领域广泛应用,为这门学科注入了巨大的生命力。
1976年,美国密码学家迪菲和赫尔曼在《密码学的新方向》一文中提出了一个崭新的思想,认为不仅加密算法本身可以公开,甚至加密用的密钥也可以公开,但这并不意味着保密程度的降低,因为加密密钥和解密密钥不一样,将解密密钥保密就可以,这就是著名的公钥密码体制。若存在这样的公钥体制,可以将加密密钥像电话簿一样公开,那么任何用户想经由其他用户传送加密信息时,都可以从这本密钥簿中查到该用户的公开密钥,用它来加密,而接收者能用只有它所具有的解密密钥得到明文,任何第三者都不能获得明文。1978年,美国麻省理工学院的里维斯特、沙米尔和阿德曼提出了RSA公钥密码体制,它是第一个成熟的、迄今为止理论上最成功的公钥密码体制。该体制的安全性基于数论中的大素数因子分解,该问题是数论中的一个困难问题,至今没有有效的算法,这使得该体制具有较高的保密性。在现代密码学中,除了信息保密外,还有另一方面的要求,即信息安全体制还要能抵抗对手的主动攻击。所谓主动攻击,指的是攻击者可以在信息通道中注入自己伪造的消息,以骗取合法接收者的信任。主动攻击可能是篡改信息,也可能是冒名顶替,这就导致了现代密码学中认证体制的产生。该体制的目的就是保证当用户收到一个信息时,能验证消息是否来自合法发送者,同时还能验证该信息是否被篡改。在许多场合,如电子汇款中,能对抗主动攻击的认证体制甚至比信息保密还重要。
2.密码学相关概念
加密是将原始数据〔明文(Plaintext或Cleartext)〕转化成一种看似随机的、不可读的形式〔密文(Ciphertext)〕。明文是一种能够被人理解(文件)或者被机器理解(可执行代码)的形式。明文一旦被转化为密文,不管是人还是机器都不能正确地处理它,除非它被解密。加密的作用是使机密信息在传输过程中不会泄露。
解密是将密文恢复出原明文的过程。
能够提供加密和解密机制的系统统称为密码系统,它可由硬件组件和应用程序代码构成。密码系统使用一种加密算法,该算法决定了这个加密系统简单或复杂的程度。大部分加密算法是复杂的数学公式,这种算法以特定的顺序作用于明文。
加密算法使用一种秘密的数值,称为密钥(通常是一长串二进制数),密钥使算法得以具体实现,其作用是用来加密和解密。算法(Algorithm)是一组数学规则,规定加密和解密是如何进行的。许多算法是公开的,而不是加密过程的秘密部分。加密算法的工作机制可以是保密的,但是大部分加密算法被公开,并为人们所熟悉。如果加密算法的内在机制被公开,那么必须有其他的方面是保密的。被秘密使用的一种众所周知的加密算法就是密钥(Key)。密钥可以由一长串随机位组成。一个算法包括一个密钥空间(Keyspace),密钥空间是一定范围的值,这些值能被用来产生密钥。密钥就是由密钥空间中的随机值构成的。密钥空间越大,那可用的随机密钥也就越多,密钥越随机,入侵者就越难攻破它。例如,如果一种算法允许2位长的密钥,算法的密钥空间就是4,这表明了所有可能的密钥的总数。这个密钥空间太小,攻击者很容易就能找到正确的密钥。大的密钥空间能允许更多的可能密钥。加密算法应该使用整个密钥空间,并尽可能随机地选取密钥空间中的值构成密钥。密钥空间越小,可供选择的构成密钥的值就越少。这样,攻击者计算出密钥值、解密被保护的信息的机会就会增大。当消息在两个人之间传递时,如果窃听者截获这个消息,尽管可以看这个消息,但是消息已经被加密,因此毫无用处。即使攻击者知道这两者之间用的加密和解密信息的算法,但是不知道密钥,攻击者所拦截的消息也是毫无用处的。
3.密码体制
一个密码系统(通常简称为密码体制)由以下5部分组成。
①明文空间M:全体明文的集合。
②密文空间C:全体密文的集合。
③密钥空间K:全体密钥的集合。其中每一个密钥K由加密密钥Ke和解密密钥Kd组成。
④加密算法E:一种由M到C的加密变换。
⑤解密算法D:一种由C到M的解密变换。它们之间的关系如图2.1所示。
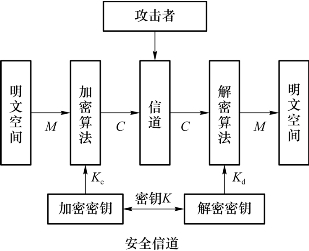
图2.1 密码体制
对于每一个确定的密钥,加密算法将确定一个具体的加密变换,解密算法将确定一个具体的解密变换,并且解密变换就是加密变换的逆变换。对于明文空间中的每一个明文M,加密算法E在密钥的控制下将明文M加密成密文C:
C=E(M,Ke)
解密算法D在密钥Kd的控制下将密文C解密出同一明文M:
M=D(C,Kd)=D(E(M,Ke),Kd)
4.密码体制的分类
通常,密码体制分为对称密码体制与非对称密码体制。如果一个密码体制的Ke=Kd,或由其中一个很容易推导出另一个,则称之为对称密码体制,否则称为非对称密码体制。对称密码体制通常又被称为传统密码体制,非对称密码体制往往又被称为公钥密码体制。图2.2给出了密码体制的基本模型。

图2.2 密码体制的基本模型
在图2.2中,消息发送者从密钥源得到密钥,通过加密算法对消息进行加密得到密文,接收者收到密文后,利用从密钥源得到的密钥,通过解密算法对密文进行解密,得到原始消息。
(1)对称密码体制
就对称密码体制而言,除了算法公开,它还有一个特点就是加密密钥和解密密钥可以比较容易地互相推导出来。对称密码体制按其对明文的处理方式,可分为序列密码算法和分组密码算法。自20世纪70年代中期美国首次公布了分组密码加密标准DES之后,分组密码开始迅速发展,使得世界各国的密码技术差距缩小,也使得密码技术进入了突飞猛进的阶段,典型的分组密码体制有DES、3DES、国际数据加密算法(IDEA,International Data Encryption Algorithm)、高级数据加密标准(AES,Advanced Encryption Standard)等。
(2)非对称密码体制(公钥密码体制)
非对称密码体制的诞生可以说是密码学的一次“革命”。公钥密码体制解决了对称密码体制在应用中的致命缺陷,即密钥分配问题。就公钥密码体制而言,除了加密算法公开,它还具有不同的加密密钥和解密密钥,其中加密密钥是公开的(称作公钥),解密密钥是保密的(称作私钥),且不能够从公钥推出私钥,或者说从公钥推出私钥在计算上是“困难”的。这里的“困难”是计算复杂性理论中的概念。
公钥密码技术的出现使得密码学得到了空前的发展。在公钥密码出现之前,密码主要应用于外交、军事等部门,如今密码在民用领域也得到了广泛的应用。1977年,为了解决基于公开信道来传输DES算法的对称密钥这一公开难题,Rivest、Shamir和Adleman提出了著名的公钥密码算法RSA,该算法的命名采用了3位发明者姓氏的首字母。RSA公钥密码算法的提出,不但很好地解决了基于公开信道的密钥分发问题,而且还可以实现对电文信息的数字签名,防止针对电文的抵赖以及否认。特别地,利用数字签名技术,我们也可以很容易发现潜在的攻击者对电文进行的非法篡改,进而实现对信息完整性的保护。公钥密码体制中的典型算法除了RSA,还有椭圆曲线加密算法(ECC,Elliptic Curve Cryptography)、Rabin、ElGamal和数论研究单位算法等。
公开密钥特别适用于Web商务这样的业务需求。公开密钥有一个非常吸引人的优点:即使一个用户不认识另一个实体,但是只要其服务器确信这个实体的认证中心(CA,Certification Authority)是可信的,就可以实现安全通信。例如,在利用信用卡消费时,根据客户CA的发行机构的可信度,服务方对自己的资源进行授权。在任何一个国家,由其他国家的公司充当CA都是非常危险的,目前国内外尚没有可以完全信任的CA机构。然而,在效率方面,公钥密码体制远远不如对称密码体制,因为它的处理速度比较慢。因此在实际应用中,往往把公钥技术和私钥技术结合起来使用,即利用公开密钥实现通信双方间的对称密钥传递,而用对称密钥来加/解密实际传输的数据。
在公钥密码体制中,加/解密密钥不同,作为信息发送者,加密者利用解密者的公钥信息加密,在收到密文后,解密者基于自己的私钥进行解密,以恢复原始消息。公钥密码体制的优点是密钥分发相对容易,密钥管理简单,可以有效地实现数字签名。
