2.2.2 分组密码

分组密码的安全分析理论
1.分组密码的原理
分组密码是将明文消息划分成长为L的分组M=(m0,m1,m2,…,mL-1),各个长为L的分组分别在密钥K=(k0,k1,k2,…,kt-1)(密钥长为t)的控制下变换成与明文等长的一组密文输出序列C=(c0,c1,c2,…,cL-1)。
分组密码的加密原理是,在密钥的控制下,通过置换,将明文分组映射到密文空间的一个分组。分组密码的原理如图2.3所示。
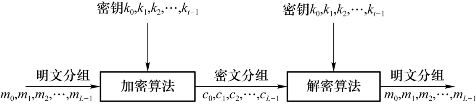
图2.3 分组密码的原理
设S是一个有限集合,f是从S到S的一个映射。如果对于任意u、v∈S,当u≠v时,f(u)≠f(v),则称f为S上的一个置换。对于一个分组长度为n的分组密码,不同的密钥应该对应不同的加密和解密变换。给定密钥k,对于任意的u、v∈S,如果u≠v,则一定有Ek(u)≠Ek(v)。因为若Ek(u)=Ek(v),则在解密时将难以准确地恢复出明文。因此,对于给定的密钥k,加密变换Ek是S上的一个置换,解密置换Dk是Ek的逆置换。
2.分组密码设计原则
对于分组密码,保证其安全性的两个设计原则是扩散和混淆。扩散和混淆是香农提出的设计密码系统的两种基本方法,其目的是抵抗密码分析者对密码体制的统计分析。
扩散,就是使明文的统计结构扩散并消失到密文的长程统计特性中,做到这一点的方法是让明文的每个数字影响许多密文数字的取值,也就是说,每个密文数字被许多明文数字影响。其结果是在密文中各种字母的出现频率比在明文中更接近平均;双字母组合的出现频率也更接近平均。所有分组密码都包含从明文分组到密文分组的变换,具体如何变换则依赖于密钥。扩散机制使得明文和密文之间的统计关系尽可能的复杂,以便挫败攻击者推测密钥的尝试。
混淆试图使密文的统计特性与加密密钥取值之间的关系尽可能的复杂,同样是为了挫败攻击者发现密钥的尝试。这样一来,即使攻击者掌握了密文的某些统计特性,由于密钥产生密文的方式非常复杂,攻击者也难于从中推测出密钥。要实现这个目的,可以使用一个复杂的替代算法,而一个简单的线性函数就起不到多少作用。
国际上著名的数据加密标准(DES)、高级加密标准(AES)和国际数据加密标准(IDEA)都是典型的分组密码算法。
3.分组密码的设计结构
现有分组密码的设计结构主要有3种:以DES算法为代表的Feistel结构及其变种结构、以AES算法为代表的SPN结构,以及以IDEA算法为代表的Lai-Massey结构。利用Feistel结构设计的算法加/解密一致、节约资源,但是扩散较慢,需要更多的迭代轮数。利用SPN结构设计的算法扩散快,一般迭代轮数较少,但往往导致加/解密不一致,从而在实现时需要更多的资源。Lai-Massey结构也具有加/解密一致的特性,其轮函数相对复杂,整体结构难于分析。近年来,基于这3种结构及其变种结构和组合结构等涌现了很多安全、高效的通用分组密码算法,除了美国AES计划和欧洲NESSFFI计划选出的算法,还有日本CRYPTREC计划中推荐的CLEFIA和MISTY1算法等,我国的商用分组密码标准SMS4算法,韩国的加密标准ARIA算法,以及其他ISO/IEC标准算法SEED和CAST-128等。这些通用算法为各个领域的安全提供了充分的保障。
另外,随着传感器网络和RFID射频网络的发展,众多轻量级的可移动设备如移动电话,智能卡,收费设备,基于RFID标签网络的动物跟踪、货物跟踪及电子护照等越来越多地应用于生活。这些设备与传统PC机相比,主要的优势是体积小、可移动、费用低,而主要的缺点是CPU计算能力有限、存储有限、电源有限,且一般要求设备的门电路数小于30 000(GE)。然而,传统的分组密码往往资源占用较大,不能很好地满足轻量级环境的要求,因此近十年来轻量级密码算法的研究成为一个热点。轻量级算法的设计和分析理论仍在探索阶段,如何在保证算法安全性的前提下尽可能降低算法的资源使用量,是分组密码学领域一个重要的研究方向。
4.分组密码的工作模式
分组密码的工作模式由以分组密码算法为基础构造的各种密码系统决定。安全的分组密码算法搭配不安全的工作模式,同样会导致密码系统不安全。
密码工作模式的主要任务是解决密钥的产生和使用问题,通常是基本密码、一些反馈和一些简单运算的组合。这些运算是简单的,因为安全性依赖于基本密码,而不是模式。工作模式不会影响算法的安全性。
1980年12月,FIPS81标准化了为DES开发的4种工作模式,包括电子密码本模式(ECB)、密码反馈模式(CFB)、密码分组链接模式(CBC)和输出反馈模式(OFB),这些工作模式可用于任何分组密码。
(1)电子密码本模式
在ECB模式中,一个明文分组加密成一个密文分组,每个明文分组都可被独立地进行加/解密,因而对整个明文序列的加/解密可以以随机的顺序进行,这对于加/解密以随机顺序存储的文件,如数据库,是非常重要的。但是因为相同的明文分组永远被加密成相同的密文分组,因此在理论上制作一个包含明文和与其相对应的密文的密码本是可能的,如果密码分析者掌握着大量的明密文对,分析者就可以在不知道密钥的情况下解密出部分明文消息,从而为进一步解密提供线索。
(2)密码反馈模式
在CFB模式下,加/解密过程由一个初始向量y0=IV开始,通过加密前一密文分组来产生当前分组的密钥流元素zi,即
zi=ek(yi-1),i≥1
同时定义
yi=xi⊕zi,i≥1
图2.4和图2.5给出了CFB模式的描述。在CFB模式和接下来描述的OFB模式下,加密函数ek被同时用于加密和解密过程。
CFB模式会产生错误扩散。通常情况下,n位CFB模式中的一个密文错误会影响当前和随后的m/n-1个分组的解密,其中m是分组大小。
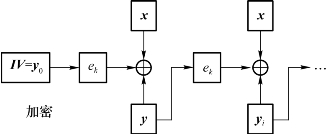
图2.4 CFB模式加密
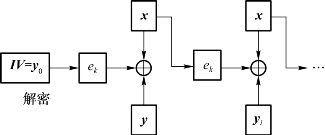
图2.5 CFB模式解密
(3)密码分组链接模式
CBC模式的基本原理如下。
假设密钥为k,明文为M=m1m2m3…mn,密文为C=c1c2c3…cn,其中,mi和ci为(0,1)序列,mi和ci的分组长度为分组密码算法的分组长度。
CBC模式的加密和解密如图2.6和图2.7所示。在该模式下,每个明文块mi首先与前一个密文块ci做异或操作,然后用密钥k进行加密。每一分组的加密都依赖于前面所有的分组。在处理第一个分组时要与一个初始向量IV进行异或运算。IV不需要保密,它以明文的形式与密文一起传送。CBC模式的算法可表示如下。
加密:c1=Ek(m1⊕IV),…,ci=Ek(mi⊕ci-1),i=2,3,4,…,n。
解密:m1=Dk(c1)⊕IV,…,mi=Dk(mi)⊕ci-1,i=2,3,4,…,n。
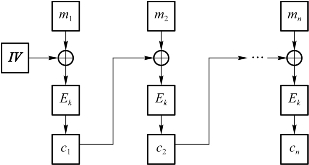
图2.6 CBC模式加密
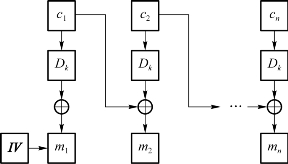
图2.7 CBC模式解密
CBC模式的优点在于引入了随机的初始向量。如果加密算法E是伪随机的,则输出具有一定的随机性,避免了ECB的缺点,隐蔽了明文的数据模式,在一定程度上能防止数据被篡改。
CBC模式的缺点在于,如果明文分组中的1 bit出错,将影响该分组的密文后面所有密文的分组。如果密文分组中的1 bit出现错误,将会影响到错误分组后的第二个分组的明文,其他的分组不受影响,但是如果密文序列中丢失1 bit,那么所有后续分组要移动1 bit,并且解密将全部错误。加密消息的长度只能是分组长度的倍数,不是任意长度。
(4)输出反馈模式
OFB模式是将分组密码作为同步序列密码运行的一种方法,它与CFB模式类似,不同之处是OFB是将前一个n位输出分组送入队列最右端的位置,解密是其逆过程。在加/解密两端,分组算法都以加密模式使用,这种方法有时也叫作内部反馈(Internal Feedback),因为反馈机制独立于明文和密文而存在。
4种工作模式的安全性、效率和容错性如图2.8所示。
