2.3.2 RSA算法
1976年,Diffie和Hellman提出了指数密钥交换的概念。1977年,Rivest、Shamir和Adleman发明了用于数字签名算法或密钥交换算法的RSA算法,这是第一个公钥密码系统。RSA算法发布不久,Merkle和Hellman就设计了一种基于背包算法的公钥加密系统。RSA密码系统与D-H密钥交换系统类似,在模数算法中使用取幂运算进行加密和解密,不同的是RSA对合数进行运算。RSA是目前世界上使用最广泛的,也是被研究得最多的公钥算法,从提出到现在已40多年,经历了各种攻击的考验,逐渐为人们接受,被普遍认为是目前最优秀的公钥方案之一。RSA的安全性取决于大数进行因式分解的难度,其公钥和私钥是一对大素数的函数。由一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积,这是公认的数学难题。RSA的速度无法胜过DES,因为DES的速度比软件中的RSA快100倍。
1.RSA中的密码学基础知识
密码学实质上体现了数论知识的应用,每一个加密算法体现了不同的加密理论,而加密理论又涉及了数论知识。所以,数论知识是加密算法的基础。
定义1(互质关系) 如果两个正整数,除1以外,没有其他公因子,则称这两个数是互质关系,即互素。
两个正整数互素的性质:①任意两个质数构成互质关系;②假设有个质数,后面找到一个数不和前面那个质数成倍数关系,则它们就互质;③所有的自然数和1都互质;④p是大于1的整数,则p-1和p构成互质关系;⑤p是大于1的奇数,则p和p-2构成互质关系。
定义2(欧拉函数) 设n为正整数,以φ(n)表示不超过n且与n互素的正整数的个数,则φ(n)为n的欧拉函数值。
定理1(欧拉定理) 如果a和n两个正整数是互质关系,那么n的欧拉函数φ(n)满足aφ(n)=1(mod n)。该式说明,a的φ(n)次方除n后的余数是1。
定理2(费马小定理) 设p为素数,对于任意整数a,ap-a是p的倍数,用模算数等式表示为ap=a(mod p),如果a不是p的倍数,则有
ap-1=1(mod p)
定义3(模反元素) 如果两个整数a和n互质,那么一定可以找到整数b,使得ab-1能被n整除,即
ab=1(mod n)
2.RSA算法
RSA算法由密钥生成、加密和解密3个部分组成。具体算法流程如下。已知公钥e和模量n,解密的私钥d必须通过因式分解n才能得到。
(1)密钥生成
①选择两个大素数p和q,计算模量n,即两个素数的乘积:
n=p×q
②选择加密密钥e,使其满足1<e<φ(n),使得e和φ(n)互质,即
gcd(e,φ(n))=1
其中φ(n)=(p-1)(q-1)为欧拉函数。
注:gcd()函数用来计算两个数的最大公约数。
③使用欧几里得算法,解密的私钥d可以通过取e的逆元来计算
d=e-1(modφ(n))
解密私钥d和模数n也是相对素数。
注:由于gcd(e,φ(n))=1,则d一定存在。
④取序对(e,n)为公钥,可公开;(d,n)为私钥,对外保密。
(2)加密
将要发送的字符串分割成长度为m<n的分组,然后对分组m进行加密,可以通过下面的加密公式找到对应的密文c:
c=me(mod n)
(3)解密
收到密文c后,接收者使用自己的私钥执行解密运算,取c的d次方得到明文m,所用解密公式如下:
m=cd(mod n)
由于欧拉公式为mφ(n)=1,因此消息m与n互质,使得gcd(m,n)=1。由于对于某个整数λ有mλφ(n)=1(mod n),该公式可以写成mλφ(n)+1=m(mod n)。因为mλφ(n)+1=m mλφ(n)=m(mod n),所以我们可以恢复消息m。
图2.26和表2.4对用于加密和解密的RSA算法进行了说明。
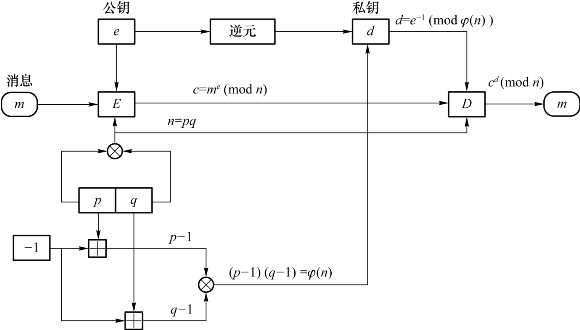
图2.26 用于加密和解密的RSA算法
表2.4 RSA算法

3.算法特点
RSA算法的优点是保密性好,安全可靠。它的不足则在于算法数据量大,使得运算时间长、效率低。因此RSA算法更适合应用于对小信息量数据的保护,采用配合其他算法共同使用的方式进行信息保护,能够提高信息保护的性能和效率。
4.总结
在数字时代,信息为社会的繁荣和发展提供着强大的力量。信息作为交流的媒介和资讯的载体,它的安全成为日趋重要的议题。随着网络特别是移动互联网的发展,连接终端数量递增,网络的应用也越来越普及,这使得每时每刻都有大量的信息在传递,信息安全面临着更大的压力。加强信息保护应该从传输系统和信息自身出发,双管齐下。既要加强各种信息系统的安全性,又要加强信息的安全性。RSA算法作为非对称加密算法,能够提高信息的安全性,为数字时代的发展提供可靠的保障;其运算量大,存在效率低的缺点,配合其他加密算法共同使用,能够使信息保护的措施更加先进和完善。
