2.2.4 对称密码的算法
1.DES算法
DES算法是从IBM在1970年年初开发出的一个叫Lucifer的算法发展起来的,Lucifer是一个包含类似于DES构造模块的代替-置换网络。在DES中,函数的输出与前一轮的输出进行异或后,作为下一轮的输出。DES算法是一个分组加密算法,以64位为一组对数据进行加密,输入64位明文,用DES加密后输出64位密文。
(1)DES整体描述
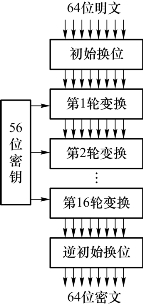
图2.12 DES的加密过程
DES对需要加密的数据进行操作,分为3步。首先将输入的密文进行分组,每组为64位。通过一个初始置换IP,针对每组64位的输入M,输出W=IP(M)。然后将64位的输入分为左右两部分,每部分32位。进行16轮的轮加密运算,其中轮密钥为48位,在第16轮中交换输出的左右两部分的次序。最后,经过一个逆初始置换IP-1,Z=IP-1(W)=IP-1(IP(M)),产生64位的密文。加密过程如图2.12所示。
(2)DES单轮函数
在每一轮中,密钥通过移位和置换选择产生新一轮的子密钥。通过E表扩展置换数据,右半部分32位扩展成48位,与每一轮生成的48位的子密钥异或,通过8个S盒进行代换、选择运算生成新的32位数据,新的32位数据再通过P盒置换一次。通过P盒的输出与数据的左半部分32位进行异或运算,成为新的右半部分32位的数据。原来的右半部分成为新的左半部分32位的数据。每轮变换可由以下公式表示:
Li=Ri-1
Ri=Li-1⊕F(Ri-1,Ki)
DES加密算法的单轮结构如2.13所示,单轮加密过程详述如下。
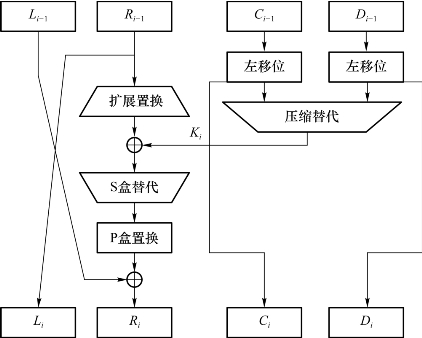
图2.13 DES加密算法的单轮结构
1)扩展置换E
扩展置换是将输入的32位块扩展成48位的输出块。它产生了与密钥同长度的数据,与密钥进行异或运算,产生了更长的结果,使输出块在代替运算时能进行压缩。具体操作为先把32位分成8个4位的块,第i块向左、向右各扩展一位,其中左扩展位与第i-1块的最右一位相同,右扩展位与第i+1块的最左一位相同。置换后的结果如图2.14所示。
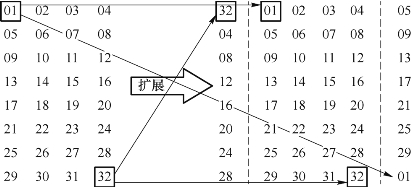
图2.14 扩展置换
2)压缩替代S(经过异或操作后)
密钥与扩展分组异或以后,将48位的结果进行替代运算。替代由8个替代盒(S盒)完成。48位的块通过S盒压缩到32位。48位的输入被分为8个6位的分组,每一分组对应一个S盒替代操作:每一个S盒都有6位输入、4位输出,且这8个S盒是不同的,如图2.15所示。
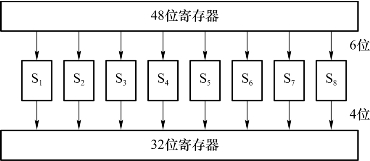
图2.15 S盒替代
每个S盒是一个4行、16列的表。盒中的每一项都是一个4b的数。S盒的6b输入确定了其对应的输出在哪一行、哪一列。假定将S盒的6b的输入标记为b1,b2,b3,b4,b5,b6,则b1和b6对应0~3,由此可选择表中的一行;b2和b5对应0~15,由此可选择表中的一列。具体见表2.2。
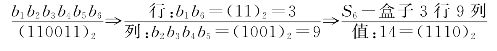
表2.2 S盒变换
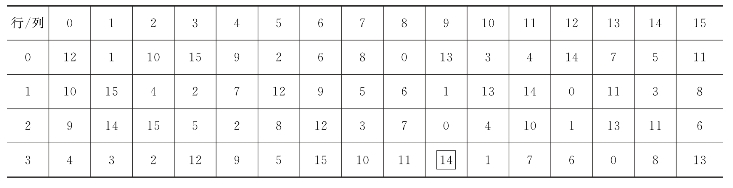
DES中其他算法都是线性的,而S盒运算则是非线性的,S盒不易于分析,但它提供了更好的安全性,所以S盒是算法的关键所在。S盒提供了密码算法所必需的混淆作用;改变S盒的一个输入位至少要引起两位的输出改变,具体如图2.16所示。
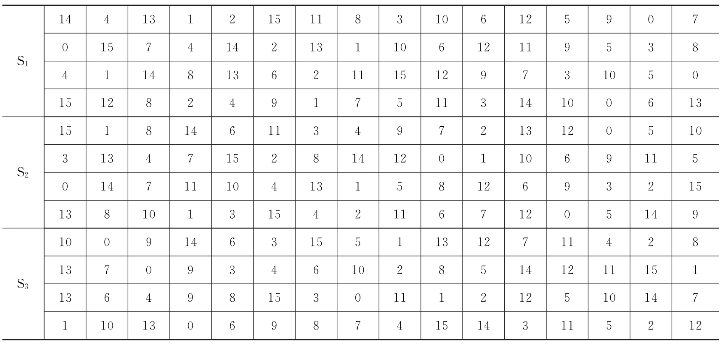
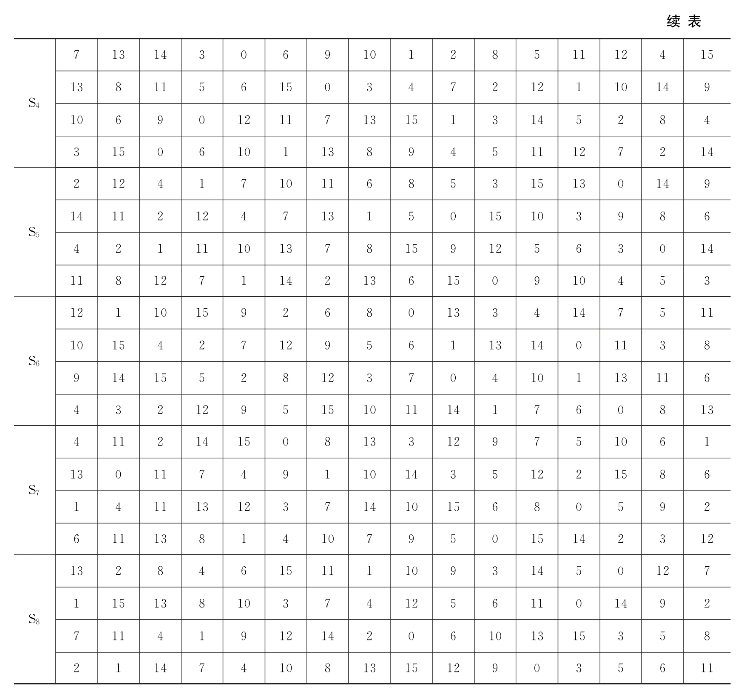
图2.16 8个S盒
3)P盒置换
P盒置换使一个S盒的输出对下一轮的多个S盒产生影响,形成雪崩效应(Avalanche Effect):明文或密钥的一点小的变动都能引起密文的较大变化。
如果变化太小,就可能找到一种方法来减小有待搜索的明文和密文空间的大小。如果用同样的密钥加密只差1位的两个明文,3次循环以后密文有21位不同;16次循环后有34位不同。如果用只差1位的两个密钥加密同样的明文,3次循环以后密文有14位不同,16次循环后有35位不同。将P盒置换的结果与最初的64位分组的左半部分异或,接着开始另一轮循环。
已知主密钥为64位(其中每个字节的第8位作为奇偶校验位),略去奇偶校验位,DES的密钥由64位减至56位,对这56位密钥进行如下置换(置换选择1),经过置换后的56位密钥被分成左右两部分,每部分28位。
①循环左移:每轮中,这两部分分别循环左移1位或2位。表2.3给出了每轮移动的位数。
表2.3 每轮移动的位数

②压缩置换(也称为置换选择2):将56位密钥压缩成48位(如图2.17所示)。置换,例如,原第14位在输出时移到了第1位;压缩,第9,18,22,25位以及第35,38,43,54位均被略去。

图2.17 压缩置换
图2.18为子密钥产生的过程。
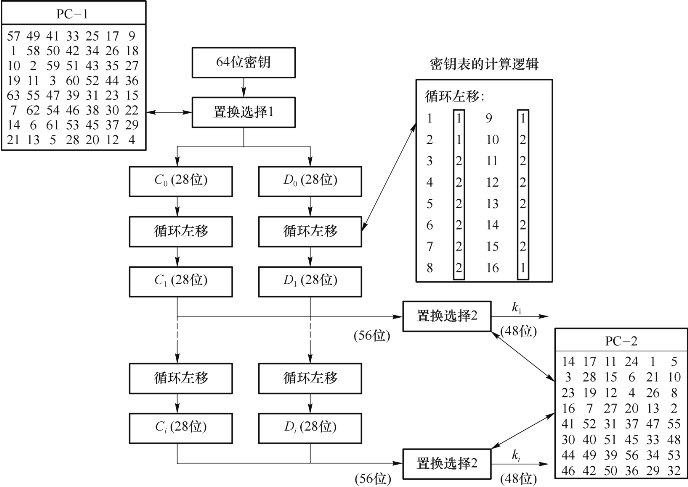
图2.18 子密钥产生的过程
4)将变换后左右两部分合并在一起
5)逆初始变换,输出64位密文(如图2.19所示)
(3)DES的解密过程
在经过所有的替代、置换、异或和循环移动之后,获得了这样一个非常有用的性质:加密和解密可使用相同的算法。
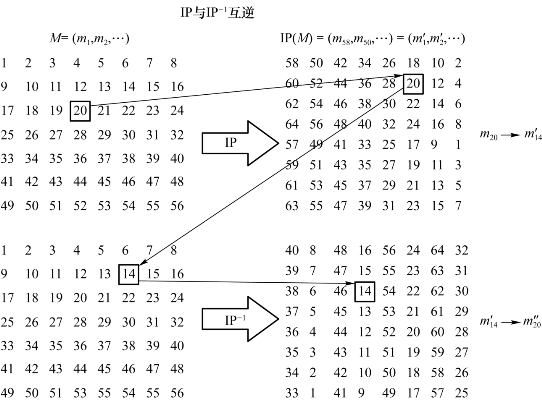
图2.19 初始变换的逆过程
DES的解密结构与其加密结构是对称相似的,使得用户能用相同的函数来加密或解密每个分组。二者的唯一不同之处是密钥的次序相反。这就是说,如果各轮的加密密钥分别是K1,K2,K3,…,K16,那么解密密钥就是K16,K15,K14,…,K1。为各轮产生密钥的算法也是循环的。密钥向右移动,每次移动位数为0,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1。
2.AES算法
1997年,美国国家标准与技术研究所(NIST)发布公告征集新的加密标准以取代旧的DES和3-DES而成为联邦信息处理标准(FIPS),这种新的算法被称为高级加密标准(AES),它被要求具有128位的分组长度,并支持128,192和256位的密钥长度,而且要能在全世界范围内免费得到。
AES的遴选过程以公开性和国际性闻名:3次候选算法大会和官方请求公众评审为候选算法意见的反馈、公众讨论和分析提供了足够的机会;15个候选算法的作者来自不同的国家,这正表明了算法的国际性,最终选作AES的Rijndael就是由比利时研究者提出的。
AES候选算法依据3条主要原则进行评判:安全性、代价、算法与实现特性。其中,安全性是评判准则中最重要的(如果一个算法被发现存在安全性问题,就不会再被考虑),同时也是最难评估的。代价指的是各种实现(软件、硬件和智能卡)的计算效率(包括速度和存储要求)。算法与实现特性包括算法的灵活性、简洁性及其他因素。
最后,在2000年10月,NIST正式宣布将Rijndael不加修改地作为AES,并在其报告中提到:无论使用反馈模式还是无反馈模式,Rijndael在广泛的计算环境中硬件和软件的实现性能都表现出始终如一的优秀。它的密钥建立时间极短,且灵敏性良好。Rijndael极低的内存需求使它非常适合于在存储器受限的环境中使用,并且能够表现出良好的性能。Rijndael的运算使其易于抵抗强力和时间选择攻击。此外,无须显著地降低Rijndael的性能就可以提供对抗这些攻击的抵抗力。
事实上,虽然Rijndael被宣布“不加修改地”作为AES,但它还是与真正的AES存在着区别。在本书后面的论述中,在没有特别说明的地方,将不加区别地使用Rijndael和AES这两个词。
(1)AES算法的总体结构
Rijndael是具有可变分组长度和可变密钥长度的分组密码,其分组长度和密钥长度均可被独立地设定为32位的任意倍数,最小为128位,最大为256位;而被AES采纳的Rijndael将分组长度固定为128位,而且仅支持128,192或256比特的密钥长度。轮数Nr依赖于密钥长度,Nr=10,12,14分别对应于128,192,256位的密钥长度。算法的总体执行过程如图2.20所示,具体步骤如下。
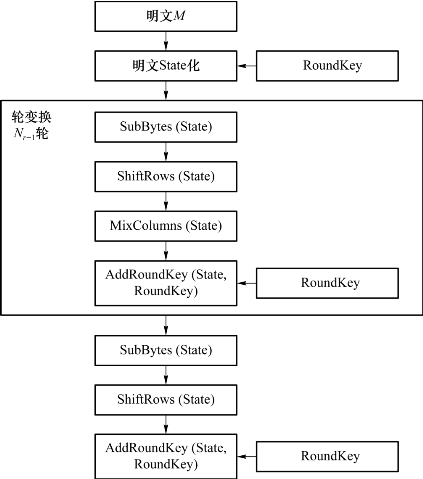
图2.20 AES算法执行过程
①给定明文x,将变量State初始化为x,并进行Add Round Key操作,将Round Key与State异或。
②对前Nr-1轮中的每一轮,用S盒对State进行一次代换操作,称为SubBytes;对State做一次置换,Shift Rows;再做一次操作,Mix Columns;然后再执行Add Round Key操作。
③在最后一轮,依次执行SubBytes、ShiftRows和Add Round Key操作。
④将State作为密文y输出。所有AES中的操作都是字节操作,明文x包含16个字节x0,Λ,x15,状态State用4×4矩阵表示:

然后将State与明文x相对应,得
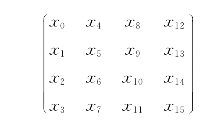
(2)Rijndael中的4种变换及设计原则
1)SubBytes
SubBytes是AES中唯一的非线性变换,它包含一个作用在状态字节上的S盒,这里用RDS表示。RDS的设计应考虑非线性度、数学复杂度等因素,本书中所采用的S盒由下式定义:
g:a→b=a-1
据此,将S盒构造为g和一个可逆仿射变换f的组合。f对S盒的非线性度没有影响,但适当地选择f可以使S盒的代数表达式非常复杂。我们选取了如下的仿射变换:
![]()
其中c=[c7c6c5c4c3c2c1c0]=[63h]=[01100011b]。它本身的描述非常简单,但与g复合后构成的代数式则非常复杂,且不存在不动点和反向的不动点:
S[a]⊕a≠00,∀a
S[a]⊕a≠FF,∀a
该仿射变换的矩阵形式如下:
b=f(a)

图2.21为S盒的变换表,输入为x和y的组合,输出为表中的项。
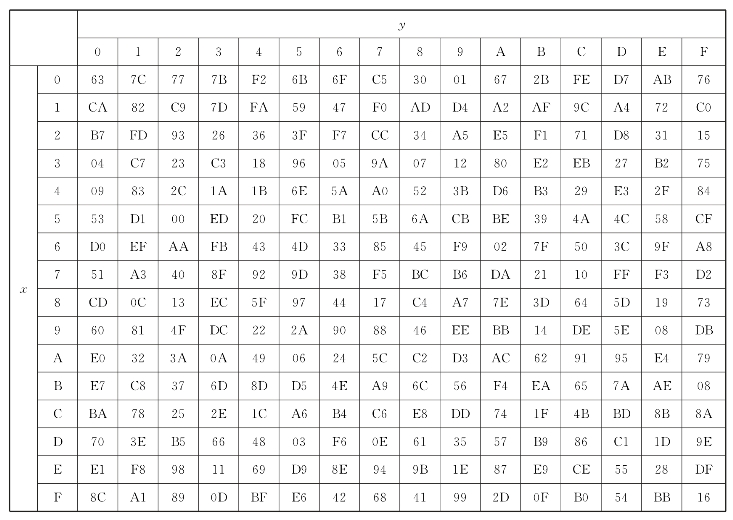
图2.21 S盒的变换表
2)Shift Rows
ShiftRows是一个字节换位操作,它将状态中的行按照不同的偏移量进行循环移位:第0行移动C0字节,第1行移动C1字节,以此类推,从而使第i行第j列的字节移动到(j-Ci)mod Nb。Ci依赖于Nb的取值。ShiftRows过程如图2.22所示。
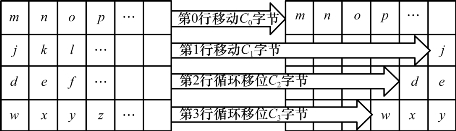
图2.22 Shift Rows过程
为了达到最佳的扩散性能(低海明重量向高海明重量扩散),4个偏移量必须互不相同。
3)Mix Columns
MixColumns对状态进行列与列的操作。将状态的列看作域GF(28)上的多项式b(x),和一个固定多项式a(x)(mod x4+1)相乘:b'(x)=a(x)⊗b(x)(mod x4+1)。用矩阵表达则为

Rijndael的设计采用宽轨迹策略,因此MixColumns应是GF(2)上的线性变换,且具有扩散能力;同时为了在查表时充分利用32位的体系结构,该步骤应是作用在4字节上的变换。
4)密钥加法
密钥加法记作AddRound Key。在这个变换中,状态的调整通过与一个轮密钥进行逐位异或得到。轮密钥记作Expand Key[i],0≤i≤Nr。轮密钥由密码密钥通过密钥编排方案导出,且与分组长度相等。Add Round Key的逆操作是其自身。
3.RC4算法
RC4算法是一种基于非线性变换的流密码算法,其内部结构可分为内部状态S盒、状态变换函数和输出函数,RC4内部状态变化如图2.23所示。
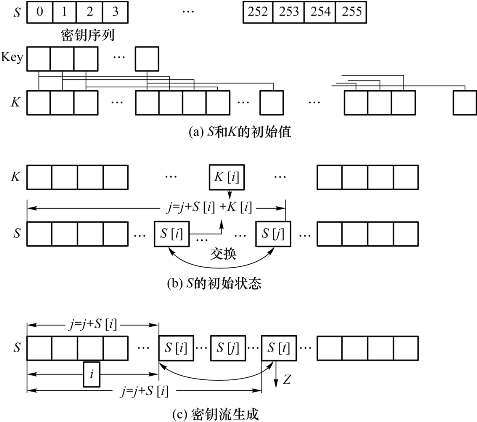
图2.23 RC4内部状态变化过程
根据运算过程,RC4算法可分为密钥编制算法(KSA)和伪随机序列生成算法(PRGA)。其中,KSA的工作原理是:设置S盒的初始排列,用可变长度的密钥生成密钥流生成器的初始状态。PRGA的工作原理是:根据初始状态进行非线性运算,选取随机元素,修改S盒的原始排列顺序,产生与明文或密文进行非线性运算的密钥流序列。
(1)KSA
RC4的KSA用于产生密钥流生成器的初始状态,步骤如下。
①随机选取一个字长为l的密钥Key,初始化S盒。
②用指针it搜索S盒中的每一个位置,it每更新一次,jt由St[it]和Key共同计算生成下一个值。
③将St中的jt和it交换。RC4的初始状态表S0由上面的KSA经过N步迭代后生成。
RC4的KSA伪代码如下。
S0[i]=i(i=0,1,…,2n-1),i0=0,j0=0;
it=it-1+1;
jt=jt-1+St-1[it-1]+K[it-1mod l];
St[it]=St-1[jt],S[jt]=St-1[it],t=1,2,…,N-1
其中,n表示算法中使用的一个字节长度;N表示长度为n的一个字节能显示值的总量,即N=2n;it和jt表示两个参数;K表示种子密钥,l为其长度,l=K的位数/n。
(2)PRGA
PRGA生成的伪随机序列构成加/解密运算的密钥流序列。伪随机序列生成原理如图2.24所示。
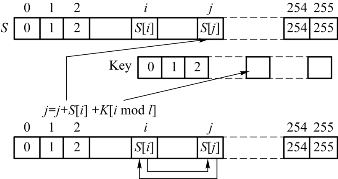
图2.24 伪随机序列生成原理
PRGA的步骤如下。
①初始化。指针it和jt的初始值在KSA产生的S0中选取。
②变换S盒。改变该算法中的j值,并将St中的it和jt进行交换。
③生成伪随机序列Z。连续改变S盒中各个字节的位置,并输出变换后的St[it]+St[jt]位置的值,该输出字节序列是伪随机序列,也是密钥流序列,记为Z={Zt}∞t=0。加密时,用Zt与明文进行异或运算,解密时同样用Zt与密文进行异或运算。
RC4的PRGA的伪代码如下。
i0=0,j0=0;
it=it-1+1;
St-1[jt]=jt-1+St-1[it];
St[it]=St-1[jt],St[jt]=St-1[it];
Zt=St[St[it]+St[jt]],t=1,2,…,N-1
其中,it和jt表示两个位置参数,Zt表示t时刻的输出值。加密时,将Zt与明文异或;解密时,将Zt与密文异或。
