与扁平龙同行
数学可以探索第四维,而这个世界是可能的,但沙皇惟有在三维世界中才能被推翻。
——弗拉基米尔·伊里奇·列宁〔10〕
维度是相当重要的。不同维度的世界之间存在巨大的差异。最简单的一种情况是二维空间的闭合曲线,它将世界分成内部和外部(见图10.3)。这个简单的内部-外部的结果极为重要。作为带管状的消化系统的二维生物来说,它使生命变得相当狂躁。如果一个平面型的人告诉你,他的生命是离析式的,你需要认真打量他,就像我们在图10.4看到的。
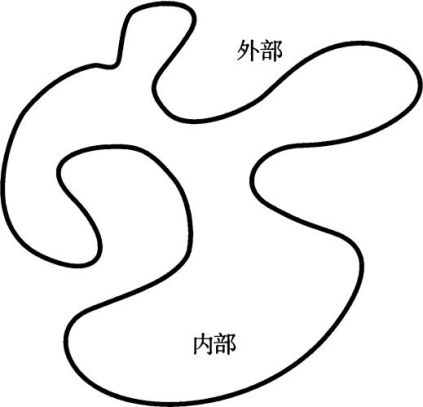
图10.3 在二维情况中,一条闭合曲线将空间分割成一个内部和一个外部。
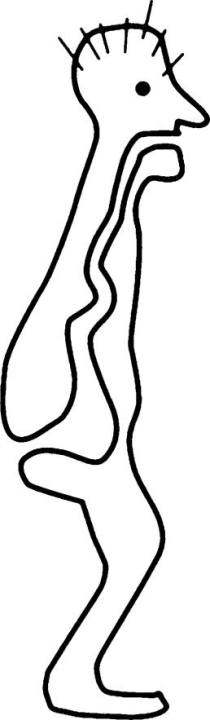
图10.4 一个具有消化系统二维的生物有可能分离。
从二维空间步入三维空间也使数学家们的生命更加有意义。在多于二维的空间里,路径会以极复杂的方式蜿蜒曲折伸展,而不会相交(见图10.5)。像斯波克先生,玩更高维度的强手棋游戏,当你把棋子放到位置上或下三维的棋子时,转到其他棋盘,各种选择会急剧增长。
实际上,三维空间是最小维数的空间,在这中间你会迷失所在。如果你在二维空间随机行走,按随机选择的方向取相同长度的步子,像一个醉汉一样,那么你最终将回到你的出发点。但如果你在三维(或更多维)空间随机行走,你绝不会回到你的出发点。你将会在空间中迷失。对于随机行走者真的存在着太多的错误转向。
这些例子说明当我们从二维进到三维和更高维度时,事情总是会变得更加复杂。但是并非必然如此。有时这额外的维度正好使事情更难配合。从柏拉图起几何学家们就认识到当我们从二维走进三维空间时,会发生某些奇怪的事。在二维有无限多数目的正(等边的)多边形,但只有五个三维的正多面体:著名的柏拉图正立体(见图10.6)。创造这类立体需要的对称性是很有要求的,且只有很少数形状能在三维空间相配合而成。对于多于三维的空间,事情仍然会有更多的限制性。

图10.5 在超过二维的空间中,路径能以极复杂方式缠绕而无须相交。
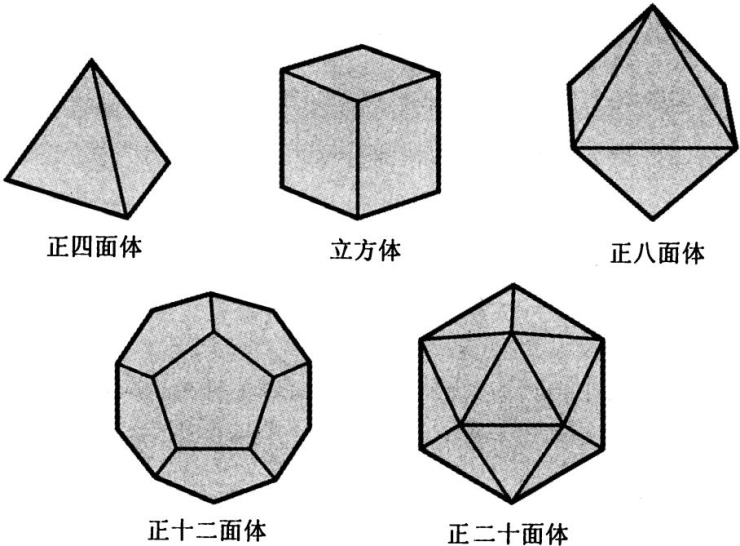
图10.6 五种柏拉图正立体。
维多利亚时代的人奇怪地受到其他维度的欺骗。他们把有关在较少或较多维度空间中的生命的幻想作品看作为寓言,通过它们提出有关三维存在的一些问题。虽然这些寓言往往具有几何学上的意义,这是它们难得的真实目的。对于一位宗教辩护士来说,为了减少对精神领域的怀疑有什么更好的方法胜过说明有福而无知的平面型的人如何可能成为对我们来说是如此平易的第三维的人呢?对于魔术师而言,如何更好地“解释”它们的魔术而不是通过乞求另一个维呢?(https://www.daowen.com)
最著名的幻想寓言,《平面帝国:一个正方形的多维浪漫故事》,这是伦敦城学院院长爱德温·艾博特于1884年写的。这是一篇蒙着薄纱的社会评论。平面帝国的人〔11〕和他们的高级教士为难了任何看不见第三维的人。人们拥有的边越多,他们的社会级别越高。因此,妇女是直线,高贵者是多边形,以及高级教士是圆形(见图10.7)。斯奎尔(正方形)先生是英雄,他遵守社会的刚性结构,直到他接待来自第三维的斯斐尔(球形)爵士的一位来访者,后来访客推动他进入第三维,以提供有关现实的性质一个更完全的视角。〔12〕
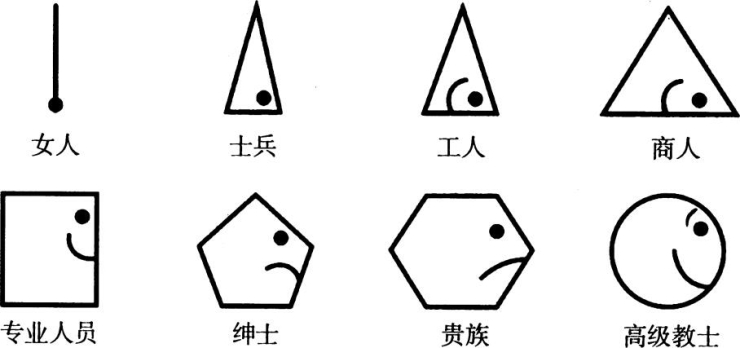
图10.7 爱德温·艾博特的平面帝国中的某些人物。
并非每个人思考过维数较少的情况。就在艾博特的著作问世前几年,伦敦社会就因1877年对臭名昭著的精神病人亨利·斯莱德的审讯受到震惊。斯莱德最终被判欺诈罪。当他宣称与第四维有接触〔13〕时,某些科学家来为他辩护,并且考察了他所说的从第四维发射客体。〔14〕神秘是维多利亚时代英国的流行观念。甚至柯南道尔似乎相信仙女。〔15〕我怀疑夏洛克·福尔摩斯是否会相信。〔16〕
在1877年进行了一些简单控制的实验以检验斯莱德所宣称的他能将客体送进送出第四维:
• 给两个完好的木环,无须将环掰开把它们相互扣住。
• 将一右旋的蜗牛壳转变为左旋的蜗牛壳。
• 在一闭合的绳环中打一个结,而不割断绳子。
• 给一绳子打上一个右手结,封在一容器内,不拆封解开结,并在绳子上打个左手结。
• 移出封在瓶里的物件,无须打开瓶子。
所有这些试验都是利用二维或三维的数学性质设计的。移走瓶内物件或解开结的唯一方法是通过进入更高维空间。如你所知,斯莱德是19世纪尤里·盖勒这类人物。天哪,他未能在控制条件下成功地完成这些拓扑学挑战的事迹,并最终由法庭定为欺骗罪。
