多边形与多配偶制

在我看来更高维空间的课题似乎正在被感觉到是严肃的问题。当我们开始对任何课题感到其严肃性时，我们也似乎部分地失去了我们处理它的专业能力。

——查尔斯·兴顿〔17〕

好奇的英国数学家查尔斯·兴顿（C.Hinton）在华盛顿特区专利事务所工作。在同一时间，爱因斯坦在瑞士专利事务所工作。他的进步党人的父亲詹姆士，曾是一位外科医生，〔18〕又是有超凡魅力的宗教哲学家，竭力鼓吹自由恋爱和公开的多配偶制；在维多利亚时代的英国，这不是进步的药方。但年轻的查尔斯似乎对多边形的兴趣甚于多配偶制。在拉格比学院和牛津大学毕业之后，他在切尔特南女子学院，后来又在乌平汉学院成为一名数学教师。他发表的第一篇论文《第四维是什么？》发表于1880年。〔19〕从此以后，他的生活变得令人窒息地激动。他曾明确地听从他的父亲的劝告，1885年因犯重婚罪而被捕。他先娶了乔治·布尔的遗孀玛丽·布尔为妻。乔治·布尔是逻辑和集合论的创建者之一。但他后来又与莫德·韦尔登结婚！坐牢三天，出狱后，他与玛丽一起去了美国，在普林斯顿被聘为讲师，他曾发明自动棒球抛球机。〔20〕从这个岗位上解聘后，他前往美国海军军官学院执教了一个时期，最后安身于美国专利局。

兴顿对较高维度的研究的一个不可磨灭的贡献是他创造了一系列的简单图形，来表示我们如何才可能得到一个看起来像是四维客体的朦胧的印象。他注意到，我们在书本中看到的实际的三维客体始终是二维的——平展于纸面上——从而我们应能预言看似四维客体的三维或二维的图形是什么样子。这个像可能是它的影子或它的投影。兴顿提出的某些例子见图10.8。

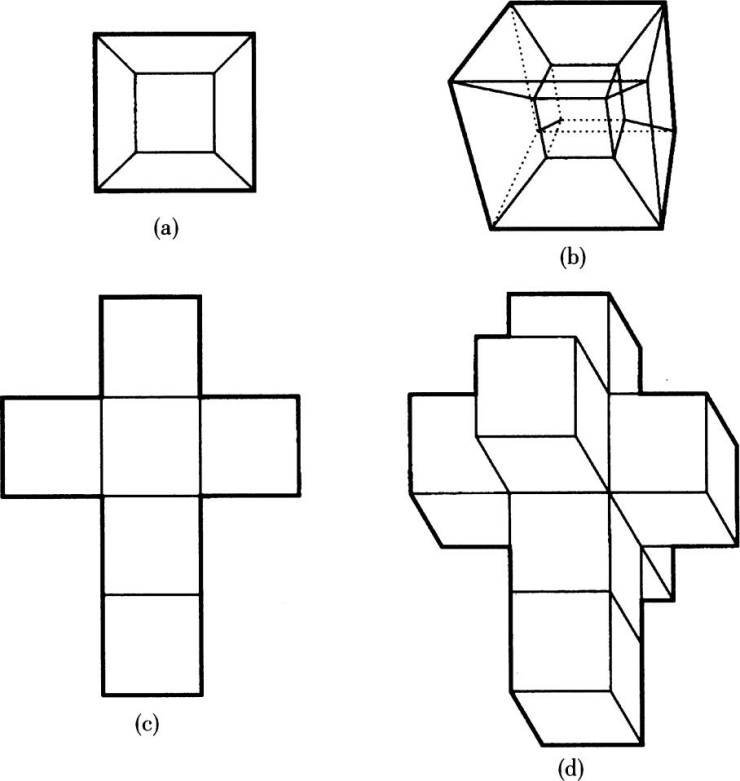
图10.8　（a）一个三维立方体当被投影时显示二维图像。（b）一个四维立方体在投影看时显出三维图，并可用透视法在纸上画出。（c）展开的一个立方体。（d）展开的一个四维立方体。

兴顿采用外推法和类似方法使第四（和更高）维形象化的思想有巨大影响，且在1909年《科学美国人》杂志为最通俗地解说第四维提供500美元的奖金。在欧洲，我们看到对多维观念的类似迷恋出现于世界艺术界。立体主义派的画家们抓住第四维。〔21〕马塞尔·杜尚的画《裸体者下楼》将一妇人走下楼梯的模糊的像叠加起来，形象表示第四维的时间。毕加索在他的《多拉·玛尔的肖像》里开拓纯粹空间的模糊性质（见图10.9）。这里的思想是摆脱单一透视的三维的严格约束，当凝视对象的面孔时，立刻用不同的角度去表现。

图10.9　毕加索的《多拉·玛尔的肖像》。〔22〕