Burgers矢量：全面优化的食品图标库

1.Burgers矢量b的确定

1）确定Burgers矢量（Burgers vector）的步骤主要如下。

（1）选定位错线的正向ξ。它是人为规定的方向，我们常选出纸面方向为正。

（2）在位错线周围任选一点（离严重畸变区适当远些的点）。用右手螺旋定则，绕位错线做右旋闭合回路。在此过程中，右手大拇指指向位错线正向，其余四指弯向绕行方向。这样，以一定步数形成的闭合回路，即为Burgers回路。刃型位错的回路不要穿过位错线；螺型位错的回路不要穿过畸变区。

（3）在不含位错的理想晶体中，以对应步数做同样的回路，起点和终点必然不闭合。

（4）连接不闭合回路的终点和起点，得到一个由终点指向起点的矢量。因为Johannes Martinus Burgers最先强调该矢量的重要性，故人们将其命名为Burgers矢量。下面，我们以此步骤分别介绍刃位错和螺位错Burgers矢量的确定。

2）刃位错中Burgers矢量的确定

如图4.16（a）所示，我们在位错线周围任选一点A作起点，出纸面方向为正。用右手拇指指向位错线正方向，则其余四指的弯曲方向为绕位错线作回路的方向，即图中沿ABCDA作的右旋闭合回路。然后我们在不含位错的晶体中，选择与图4.16（a）中具有大致相同位置的A点作起点，同样用右手螺旋作回路。在此过程中，作的步数要与含有位错的回路中作的步数对应一致，也即图4.16（a）中，AB为5步、BC为6步、CD为5步、DA为5步；同样在图4.16（b）中的AB也为5步、BC为6步、CD为5步、DE为5步。这样在不含位错的晶体中，终点E与起点A不重合。连接终点E与起点A，则EQ为图中刃位错的Burgers矢量，方向由E指向A。请读者用此方法确定一下图4.13（b）所示的Burgers矢量。

3）螺位错中Burgers矢量的确定

总体说来，前面介绍的方法，对确定螺位错中的Burgers矢量同样适用。然而，由于螺位错Burgers回路中的线路不在一个平面上（刃位错中回路的各部分都在一个平面上），所以Burgers矢量的确定相对复杂些。

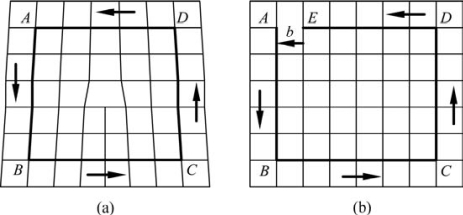
图4.16　刃位错Burgers矢量的确定示意图

（a）含位错的Burgers回路；（b）完整晶体中的回路

首先是起点的选取。我们总希望Burgers回路都出现在晶体表面，这样才容易得出Burgers矢量。因此，尽管起点的选取是任意的，但起点没有选好的话，会使回路的部分线路出现在晶体内部，这给Burgers回路的分析带来困难。此外，在含纯螺位错的晶体中，有绕位错线的一个连续性螺旋坡面，如同我们上楼的楼梯一样。这样，我们可以选择较低螺旋面旁边一侧晶面的某个点作起点。在图4.17（a）中，b处在较低螺旋面上，e处在较高螺旋面上。我们选择b旁边晶面的a点作起点。其次是位错线的正向的选取。我们先用右手四指的弯曲指向螺旋面上升方向。图4.17（a）中，这个方向是bcd到e。此时，右手拇指的指向即为位错线的正方向，即图中的出纸面方向。这样，含有螺位错的Burgers闭合回路为abcdefa。a到b有1步、b到c有8步、c到d有4步、d到e有8步、e到f有2步、f到a有4步。

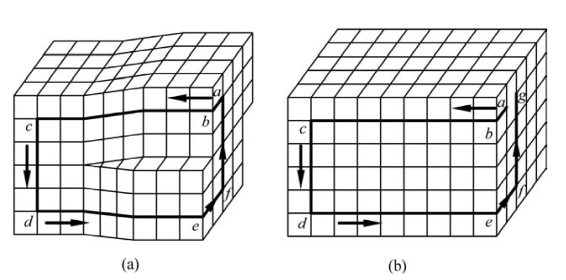
图4.17　螺位错Burgers矢量的确定示意图

（a）含位错的Burgers回路；（b）完整晶体中的回路

接下来，我们在完整晶体中还是选择与图4.17（a）中具有大致相同位置的点a作起点，见图4.17（b）。然后，按照与图4.17（a）相应的步数作回路abcdefg。这时，起点a与终点g不重合，即回路不闭合。连接终点g与起点a，则ga为此图中螺位错的Burgers矢量，方向由g指向a。ga的方向与位错线正向（即拇指指向或出纸面方向）相同，我们称之为右旋螺位错；若Burgers矢量ga的方向与位错线正向相反，则称之为左旋螺位错。

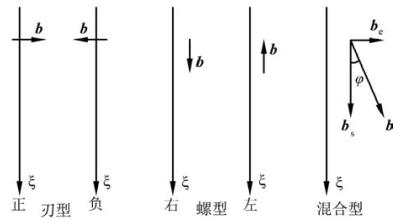
根据以上介绍的内容，人们得出了位错的普遍性定义（图4.18）：刃位错b·ξ=0。右旋螺位错b·ξ=b；左旋螺位错b·ξ=-b。混合位错的螺型分量bs=（b·ξ）ξ；bs=b cosφ。刃型分量be=［（b×ξ）·e］（ξ×e）；be=b sinφ，其中e为垂直于滑移面的单位矢量，有e=（b×ξ）/|b×ξ|。

(https://www.daowen.com)

图4.18　三种类型位错的主要特征（引自蔡珣，2010）

2.Burgers矢量的物理意义

Burgers矢量b反映了位错区域点阵畸变的总积累。b的方向代表位错运动而导致的晶体滑移方向；其模|b|表示点阵畸变的程度，即位错强度。|b|越大，则点阵畸变越大，位错区域的原子错配越严重，同时位错引起的晶体弹性能也越高。

3.Burgers矢量的表示符号

为了明确晶体中Burgers矢量b的方向及大小，人们采用了一定的符号对其进行表示。Burgers矢量的方向和大小可用它在各晶轴上的分量表示。尤其是方向与第2章中晶向指数的确定方法相同。因Burgers矢量也表示位错运动后晶体的相对滑移量，故它只能从一个原子的平衡位置指向另一个平衡位置。由此可知，最短平移矢量往往是最稳定的Burgers矢量。如果晶体的滑移是通过位错运动来实现的，则最短平移矢量的方向也代表晶体的滑移方向。关于这点，我们在前面介绍滑移时就提到过：滑移总是在原子密度大的晶面上沿原子密度大的晶向发生，因密排晶向是最短平移矢量的方向。

面心立方点阵。最短Burgers矢量为（a/2，a/2，0）。将该矢量的三个分量的公因数a/2提出来，剩下的数字用“［］”括起来，使［］内的数字为最简整数，则为a/2［110］。a/2［110］是面心立方点阵在〈110〉晶向族方向的Burgers矢量符号。对fcc晶体结构的金属，a/2［110］为｛111｝晶面和〈110〉晶向组成的滑移系统的Burgers符号；对NaCl结构的离子晶体，a/2［110］为｛110｝面和〈110〉晶向组成的滑移系统的Burgers矢量符号。这些Burgers矢量的模|b|，可用数学方法求得|b|=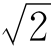a/2，其中a为点阵常数。

体心立方点阵。最短Burgers矢量为（a/2，a/2，a/2）。用与上面同样的方法将该矢量的三个分量的公因数a/2提出来后成为a/2［111］。对bcc晶体结构的金属而言，此符号表示｛110｝晶面和〈111〉晶向组成的滑移系统的Burgers矢量符号。该矢量的模|b|为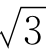a/2。

六角点阵。最短Burgers矢量为（a/3，a/3，-2a/3，0），其符号为a/3［11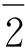0］，其模|b|为a。该矢量是｛0001｝面、〈11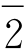0〉晶向组成的滑移系统的Burgers矢量符号。六角点阵的最短Burgers矢量请结合第2章的四轴定向和行走法确定晶向符号来理解。

以上这些最短点阵的Burgers矢量，其相应的位错称作单位位错，即晶体的滑移如果是通过位错运动来实现的，则原子在Burgers矢量方向上移动一个原子间距。若Burgers矢量为单位位错的整数倍，则对应的位错为全位错；而Burgers矢量不为单位位错的整数倍，则对应的位错为不全位错。

4.Burgers矢量的特性

1）Burgers矢量的守恒性

在确定Burgers矢量时，只要回路不穿过刃位错的位错线、螺位错的过渡区，则Burgers矢量与回路的形状、大小和位置无关。所以只要一个位错不和其他位错相交，Burgers矢量是唯一的。而且一根不分岔的位错线只有一个Burgers矢量。在此基础上，可以得出：如果几条位错线在晶体内相交（交点称为位错节点），那么“流入”节点的位错线，其Burgers矢量之和必等于“流出”节点的位错线Burgers矢量之和，即

式（4-80）表明了Burgers矢量的守恒性。现做一简单证明。

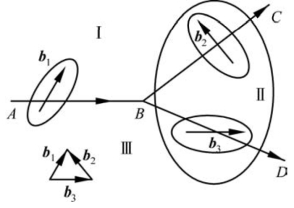
图4.19　位错线相交示意图（引自潘金生，2011）

如图4.19所示，有三条位错线AB、BC、BD相交于节点B，其Burgers矢量分别为b1、b2、b3。这三个位错分别具有各自的Burgers回路。现在，我们作一个大回路，包括b2、b3对应的位错。大回路也具有一个Burgers矢量b4。b4对应位错的畸变必然是b2、b3对应位错畸变的总和，所以b4=b2+b3。将大回路以晶格间距为单位，向节点平移。当平移至节点B时，b2、b3的综合位错线与AB相交于点B。根据前文所述，一根不分岔的位错线只有一个Burgers矢量，故b1=b4，即b1=b2+b3，也就是“流入”节点的位错线，其Burgers矢量之和等于“流出”节点的位错线Burgers矢量之和。

2）Burgers矢量的连续性

位错线要么起止于单晶体表面、多晶体的晶界，要么形成封闭回路（即位错环），也可在节点处和其他位错线相连，但不能中断于单晶体内部。

如图4.20所示，设位错线AB中止于一单晶体内的B点。则AB两侧必为已滑移区和未滑移区。设Ⅰ区为已滑移区、Ⅱ区为未滑移区。第Ⅲ区要么是已滑移区，要么是未滑移区。若Ⅲ区为已滑移区，则Ⅱ—Ⅲ区的界线BC成为已滑移区和未滑移区的分界，BC为位错线；若Ⅲ区为未滑移区，则Ⅰ—Ⅲ区的界线BD成为已滑移区和未滑移区的分界，BD为位错线。所以，AB位错线要么连接BC成为ABC位错线，要么连接BD成为ABD位错线。无论哪种情况，位错线都终止于单晶体表面。