4.6.2 牛顿迭代法
2025年09月26日
4.6.2 牛顿迭代法
【例4-26】用牛顿迭代法求a的平方根。迭代公式
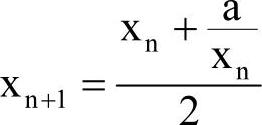
精度要求：xn+1与xn的绝对值小于0.00001。
方法描述：
用户输入a，估算a的平方根，一般估算x0为a/2，再根据x0和a代入公式计算x1，然后再用x1和a计算x2，其余类推。
“三步法”原则分析如下。
做什么
1）用户输入a，所以窗体上需要一个文本框。
2）一个“计算”按钮。
怎么做
通过分析不难得出，此问题的特点如下。
运算迭代次数是无法预知的，公式中用到了x0，x1，…，xn+1，但是在程序中是不能这样引用的。因为在程序设计代码中没有下标的概念。并且作为程序的循环结构，循环体内变量名是不能改变的。循环体的特点是采用相同的变量实现程序的循环，在循环过程中通过不断修改变量中的数据来实现一个数列表示，所以循环体内是不能用x0，x1，…，xn+1来表示的。其实整个迭代公式计算过程中只用到了3个变量xn+1、xn和a，与xn前面的数据无关，这些数据不需要保留。如果计算精度不够，只是用xn+1替换xn，然后重新计算一个xn+1。所以用x1表示xn+1，用x0表示xn。
步骤描述如下。
1）读取用户输入的数据，放入变量a中。
2）初始化x0为a/2。
3）通过公式计算x1。
4）计算x1与x0的绝对值，如果绝对值大于0.00001，则执行第5）步，否则执行第8）步。
5）用x1替换x0。
6）通过公式计算x1。
7）返回第4）步。
8）输出a的平方根x1。
实现
实现代码如图4-35所示。
图4-35 计算平方根
代码中
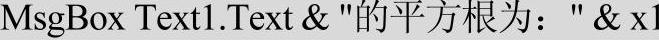
能否改为
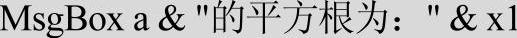
请思考此问题。
下面是采用其他结构代码。
●前测型直到型结构：
采用后测型当型结构和后测型直到型结构也能够实现，但不是最佳的，所以这里就不列出了。
●While语句实现：
