2.过程递归

2.过程递归

如果一个过程在执行过程中调用自己，则这种调用称为递归。

【例7-10】递归实现求解自然数的阶乘。

例7-6用函数实现阶乘计算，其方法是从1开始，一直乘到n。

在数学中还有另外一种定义，自然数n的阶乘为：

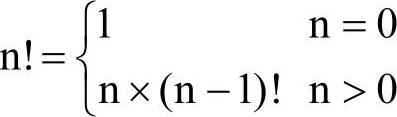
分析：

1）要计算出n的阶乘必须先计算出n−1的阶乘，而要求出n−1的阶乘，必须先求出n−2的阶乘，其余类推。直到n=0，已知0的阶乘为1。

2）已知0的阶乘，就可以计算出1的阶乘，计算出1的阶乘，就可以计算出2的阶乘，其余类推，直到计算出n的阶乘。

用递归实现代码如下：

【例7-11】递归实现汉诺塔问题。

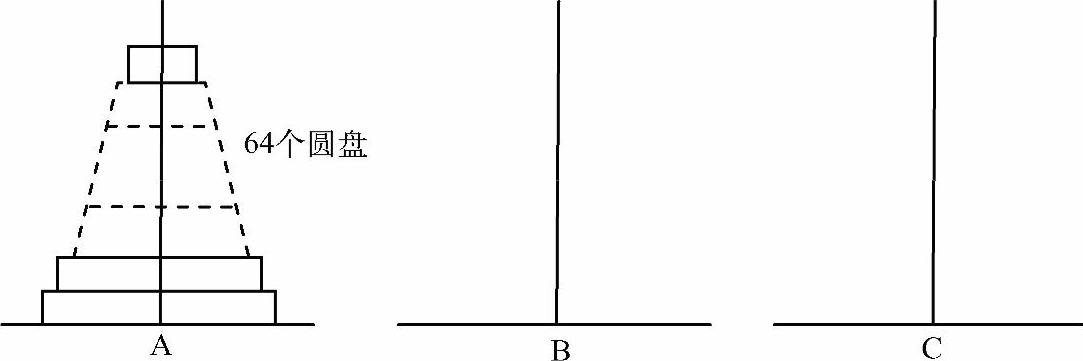
有3根柱子A，B，C。A柱上套有64个大小不等的圆盘，大的在下，小的在上。如图7-15所示。要把这64个圆盘从A柱移动C柱上，每次只能移动一个圆盘，移动可以借助B柱进行。无论何时，任何柱上的圆盘都必须保持大盘在下，小盘在上的状态。求移动的步骤。

图7-15 汉诺塔问题

分析：假设3根柱子分别命名为x，y，z，n个圆盘穿在x针上。

1）要把n个圆盘从x移动到z上，就必须先把上面n−1个圆盘从x移动到y上，这时才能把x中最下面的第n个圆盘移动到z上。

2）同样，要把n−1个圆盘从x移动到y上，就必须先把上面n−2个圆盘从x移动到z上，这时才能把x中第n−1个圆盘移动到y上。

其余类推，直到获得x中第1个圆盘的移动位置，就可以实现了。

实现如下：

运行结果如图7-16所示。

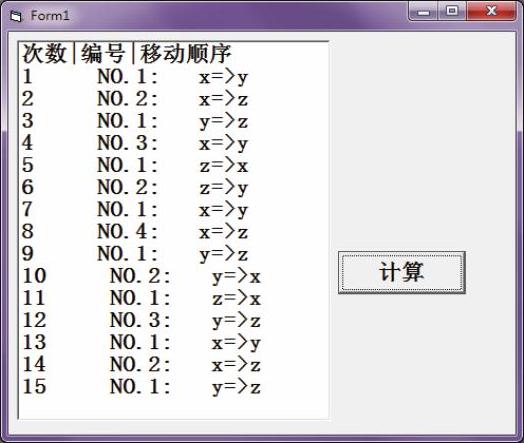
图7-16 汉诺塔

因为移动次数较多，此处使用了ListBox列表框控件。本例中，n设为4，移动次数为15。通过指定不同的n值，不难发现，移动次数为2ⁿ−1。要移动64个圆盘，需要移动2⁶⁴−1次，假如移动一次需要1秒，则共需要5800多亿年。