2.2.4 局部指标
局部指标只研究某节点或局部区域负荷增长对系统稳定的影响，大大减少了电压稳定分析计算量，计算速度快，可应用于在线分析。
1.局部负荷裕度指标
假定除第i节点以外其他节点负荷维持不变，形成i节点的等效系统，即图2-1所示两个系统的潮流值是相等的。确定等效网络的相量值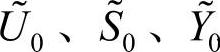
，使得潮流注入
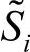和电压灵敏度
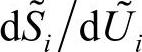对两个系统是相等的。则局部负荷裕度指标便定义为：假定在其他节点负荷维持不变的情况下，节点i的负荷功率因数不变、负荷不断增加时，从起始负荷（以MW表示的P0i）到PV曲线鼻端（以Pmaxi表示）的距离的相对值，即
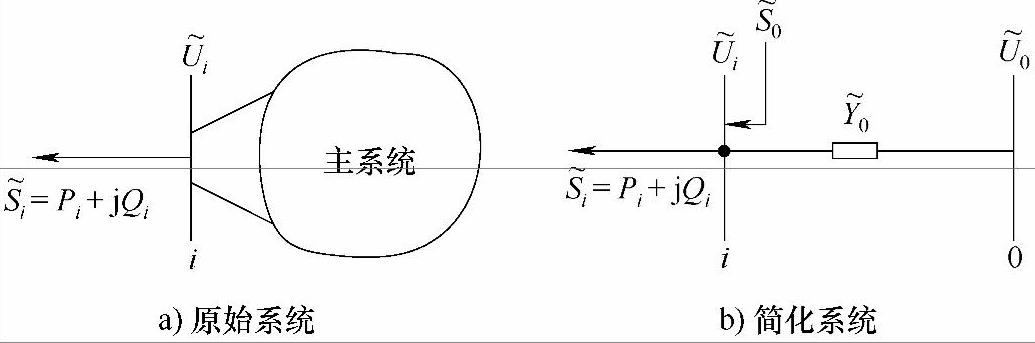
图2-1 系统简化
负荷裕度PLmgi的值在0和1之间，在崩溃点为0。当上式各功率值取相应的电压值时，上式也可以用于计算每个负荷节点的电压裕度。该方法可以推广到某区域多节点负荷增长的情况。
因为PLmgi是对具体节点定义的，所以它的计算比较容易。然而，电压稳定裕度应当对整个电力系统进行评价。这样，指标PLmgi应当对所有节点进行计算，即需要计算系统负荷节点数那么多的PLmgi，计算量很大。为此，根据图2-1推导出了一种适用于所有负荷节点PLmgi的有效估计方法。
2.负荷节点电压稳定性就地安全指标
本章参考文献[7]在讨论一种二次方程判别式指标即线路稳定因子的基础上，利用电压方程的有解判别式，又提出了两种适用于就地电压控制的节点电压稳定指标，即利用电压实部的安全指标和利用电压幅值的安全指标。
线路稳定因子原理简单，可以用来判断系统的弱节点。但是其推导存在数学问题，即没有考虑线路两节点之间的相互作用关系，而且该指标的线性程度比较差。利用电压幅值的安全指标在崩溃点处为零，线性程度比较好，计算量小，速度快。
本章参考文献[7]对安全指标的分析都是在简单系统中进行的，但必须应用到实际的复杂电力系统中，因此有必要在复杂系统中验证其有效性。考虑到对某一特定节点的电压稳定性进行分析计算采用的是就地测量值，可以将该节点以外的系统简化为系统阻抗和无穷大母线，最后得到类似于图2-1的分析系统，但参数需要辨识得到。
3.裕度指标
裕度指标是常用的静态电压稳定指标之一，其定义为：从系统给定运行状态出发，按照某种模式，通过负荷增长或传输功率的增长逐步逼近电压崩溃点，则系统当前运行点到电压崩溃点的距离（kV、MW和/或Mvar）可作为电压稳定程度的指标[6]。
相对于状态指标而言，裕度指标具有以下优点：能给运行人员提供一个较直观的表示系统当前运行点到电压崩溃点距离的量度；系统运行点到电压崩溃点的距离与裕度指标的大小呈现线性关系；可以比较方便地计及过渡过程中各种因素（如约束条件、发电机的有功分配、负荷增长方式等）的影响。因此，电压稳定裕度指标分析方法受到了广泛的关注。
负荷功率需求的持续增长、系统故障或有载调压变压器的动态调节都可以使系统从正常运行点移向崩溃点。在计算裕度指标时，网络中各负荷节点的功率可以按照任意方式增长，以逼近崩溃点。为了简化计算，常假设负荷功率以下述四种方式增长：
1）单负荷节点的有功和/或无功功率增加，其他负荷节点的功率保持不变。
2）选定区域的负荷节点的有功和/或无功功率增加，其他负荷节点功率保持不变。
3）某一选定区域的负荷节点的有功和/或无功功率增加，而另一选定区域的负荷节点的有功和/或无功功率减少，其他负荷节点功率保持不变。这在东西方向长距离输电线路中，由于时差的原因有可能出现。
4）全部负荷节点的有功和/或无功功率同时增加。
负荷的增长方式不同，裕度指标的计算结果也不相同。通常采用4）的方式进行计算。
4.阻抗模指标
如图2-2所示，由潮流方程有解的条件可知，当负荷节点的等效阻抗等于该节点网络的等效阻抗时，该网络输送功率达到极限，也就是稳定极限，因此可以在负荷节点处监视负荷阻抗以及网络等效阻抗的大小。当两者接近时，表示系统运行接近稳定极限。
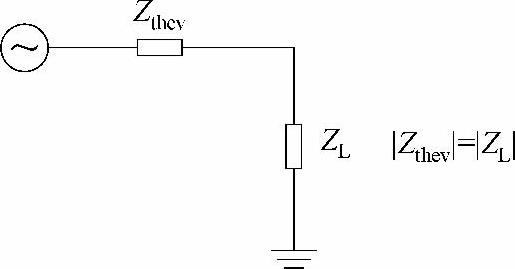
图2-2 节点等效电距离和负荷等效阻抗
节点电压静态稳定问题研究中，在运行中的某一时刻从待研究的负荷节点看向系统的等效阻抗，其大小表示节点与系统联系的紧密程度，等效电距离值越大，说明该节点离等效恒压节点越远，从而系统对该节点电压的控制越弱；等效电距离值越小，说明系统越容易控制该节点的电压。因此，阻抗模方法不但可以用于计算临界点，也可以用于弱节点的判断。
该方法线性性比较好，但是计算费时，而且由于戴维南等效带来的误差，使得计算结果有一定的偏差，从而影响了该指标的实用性。