3.9.1 计及最小电压安全裕度指标的最优潮流模糊模型
本研究的最小负荷裕度指标又可称为最小电压安全裕度指标,其详细定义见3.2节。具有硬约束和可松弛约束、计及最小电压安全裕度指标的优化问题可用以下非线性规划模型表示:
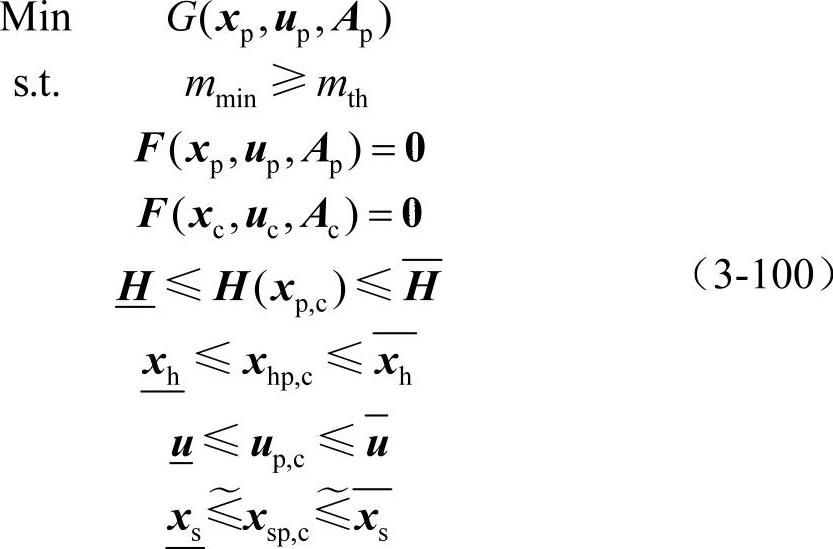
式中,目标函数G(xp,up,Ap)可以是单目标,也可以是多个子目标的联合;mmin表示系统电压安全裕度向量M(M∈R2l,l为负荷节点数)中最小的元素;mth表示系统允许的最小电压安全裕度。实际上,对于某一具体的系统而言,系统的电压稳定与否往往取决于关键发电机节点和系统薄弱节点的状态,因此,也可以采用系统薄弱节点中最小的负荷裕度代替mmin计入优化问题模型。上式中的变量向量和其他的约束条件与式(3-20)相同。
在此同样采用系统所有负荷以线性、恒功率因数持续增长的负荷增长方式进行优化研究,以最小化系统总发电成本为目标,将节点电压约束进行模糊化处理,则优化问题模型可重新表达为
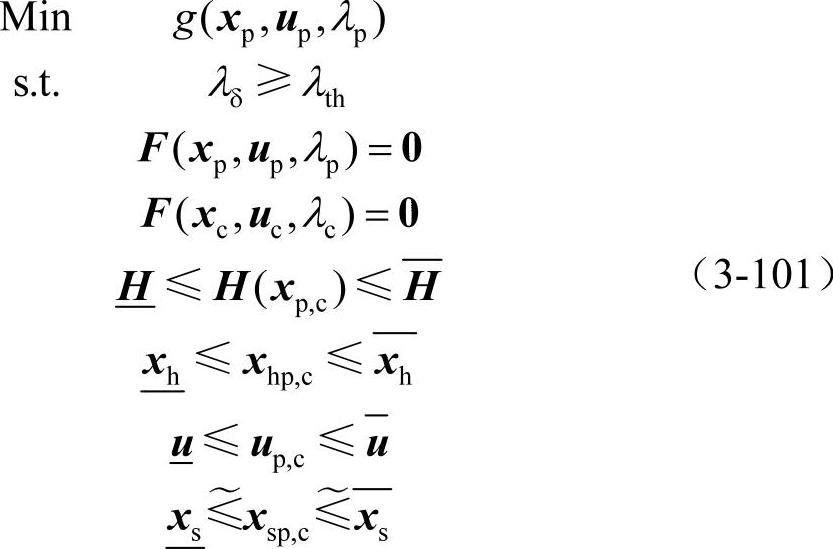
式中,λp和λc分别表示系统当前运行点和临界运行点的负荷增长参数;λδ=λc-λp表示对应于当前负荷水平的系统实际负荷裕度。
根据前面对可松弛约束进行模糊化处理的理论探讨与仿真结果显示出的有效性可以推断:系统的最小电压安全裕度指标也可应用该模糊处理方法,即对系统运行人员根据专家意见以及实践经验确定的最小电压安全裕度可进行适当模糊化处理,以防止系统优化运行解过于“保守”或过于“冒险”的极端情况出现。式(3-23)和式(3-25)已经分别给出了系统总发电成本和节点电压约束的隶属函数,图3-12和图3-14分别给出了两种隶属函数的分布曲线,现将最小电压安全裕度指标的隶属函数分段线性表示为
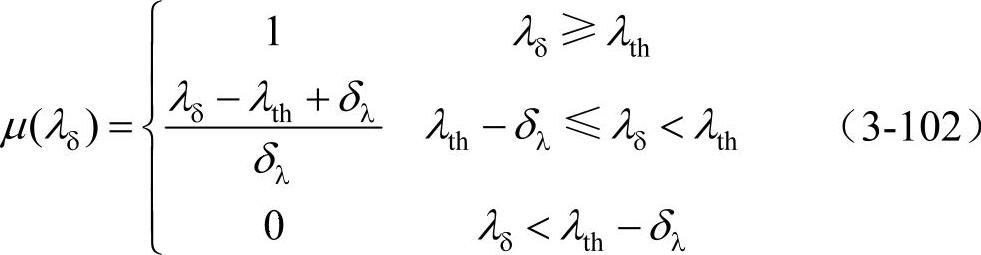
式中,δλ表示最小电压安全裕度模糊参数。对应于该隶属函数的分布曲线如图3-22所示。
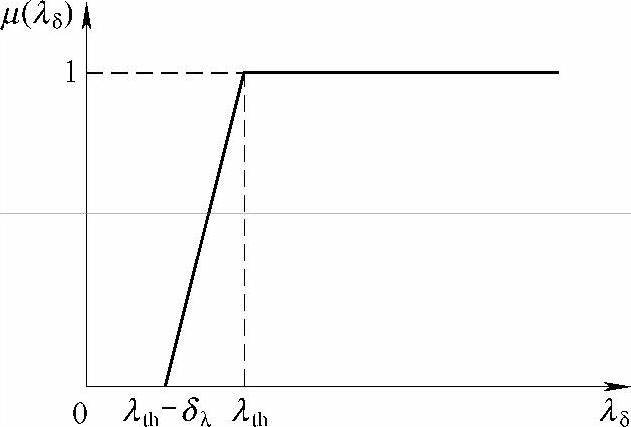
图3-22 λδ的隶属函数分布曲线
由式(3-23)、式(3-25)和式(3-102),可得满意度η为
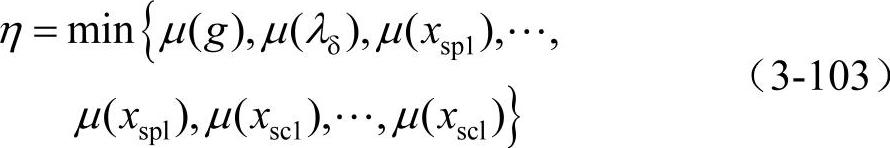
由此,原问题可转化为求满意度η最大化的最优潮流问题,其目标函数和相应约束分别表示如下:
(1)目标函数

(2)等式约束(节点潮流方程)

(3)不等式约束
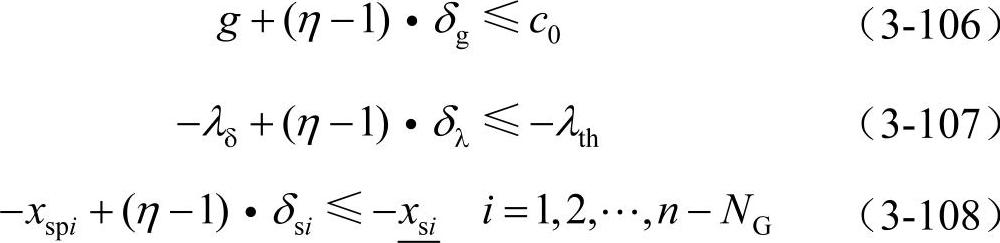
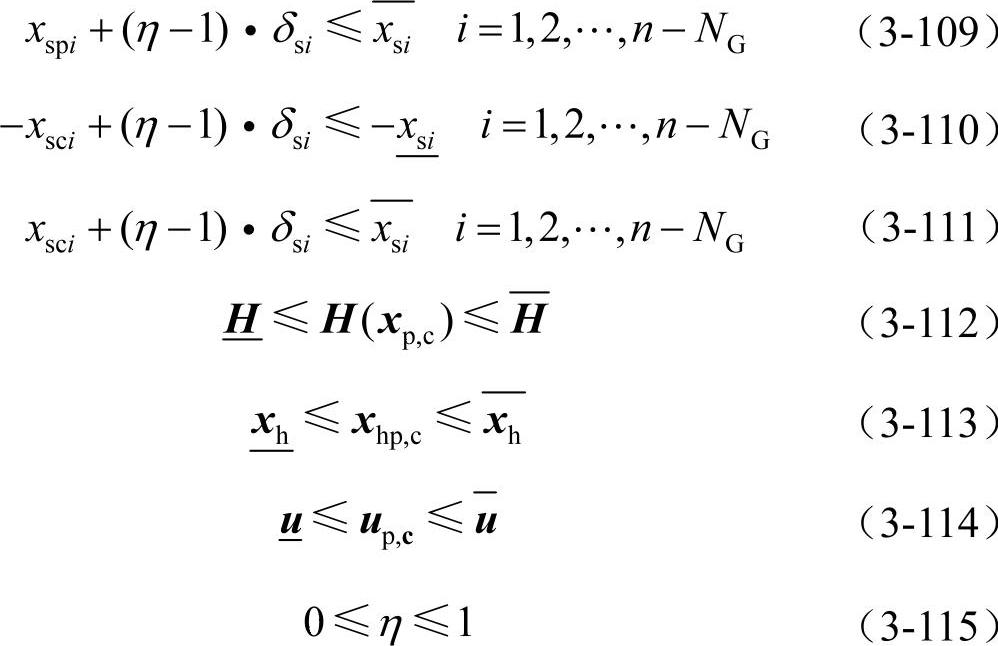
该优化问题仍采用预测-校正原对偶内点法进行求解,步骤与3.7.2节相同。
