注册结构工程师专业考试精讲

（一）支座反力影响线

如图9.2.3a所示一外伸梁，取A点为坐标原点，横坐标x以向右为正。当荷载P=1作用于梁上任一点时，由平衡方程求得支座反力为

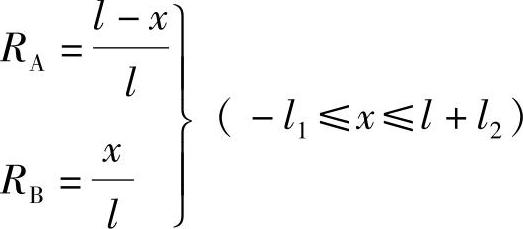
这两个支座反力的影响线方程与简支梁的相同，只是荷载P=1的作用范围有所扩大。在简支梁中，x的变化范围是0≤x≤l，这里则为-l₁≤x≤l+l₂。R_A和R_B的影响线如图9.2.3b、c所示。由图可见，AB段的影响线与简支梁的完全相同，只要将这段直线向两个外伸部分延长，即得出整个影响线。

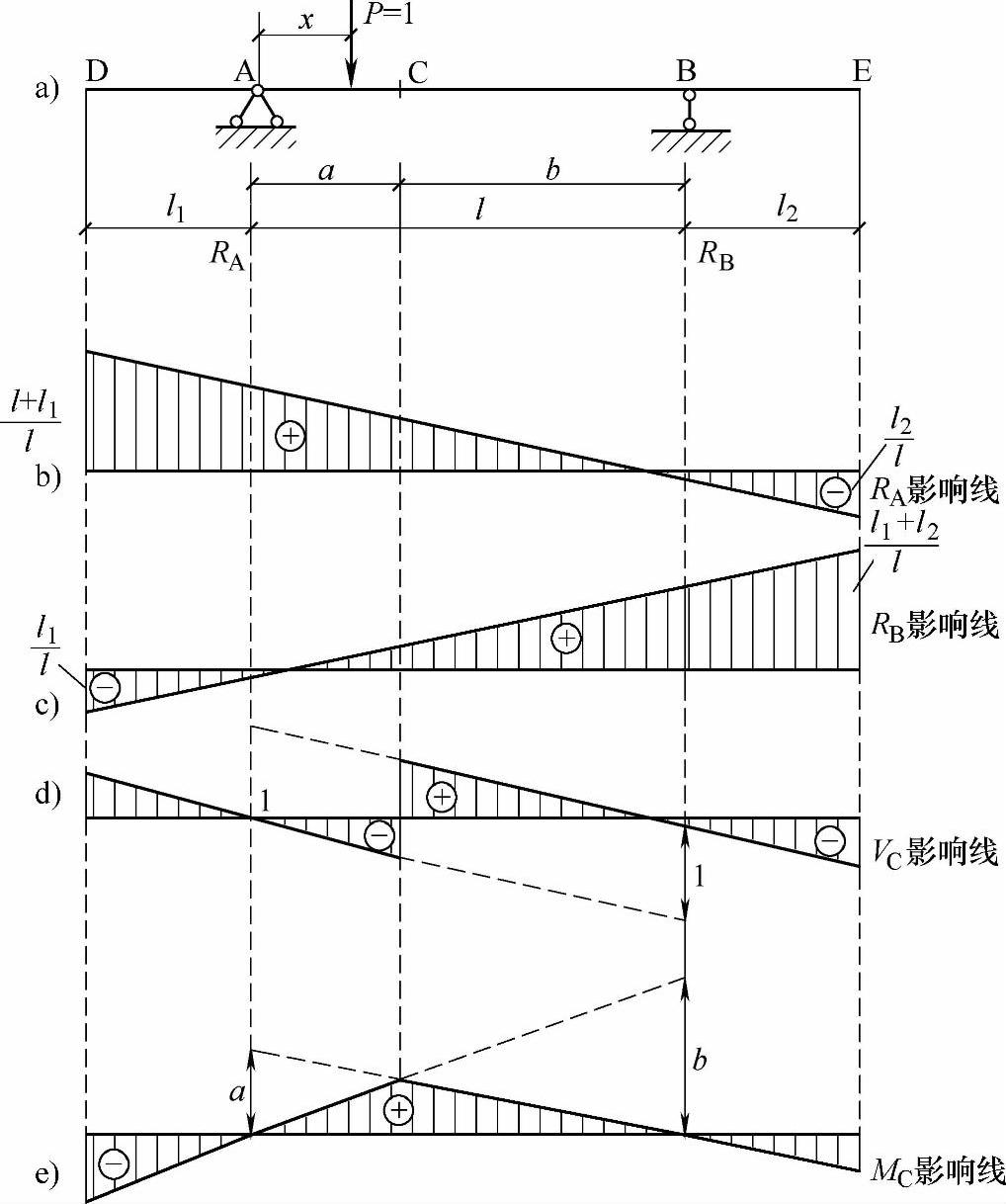
图 9.2.3

（二）跨中部分截面的内力影响线

绘制指定截面C的剪力V_C和弯矩M_C的影响线，如图9.2.3所示。当P=1在C点以左时，取截面C以右部分为隔离体，得

V_C=-R_BM_C=R_Bb

当P=1在C点以右时，取截面C以左部分为隔离体，得

V_C=R_AM_C=R_Aa(https://www.daowen.com)

由上述关系可知，V_C、M_C的影响线方程与简支梁的相同。因而只需将简支梁上相应截面的剪力和弯矩影响线向两边外伸部分延长，即可得出外伸梁的V_C和M_C影响线，它们分别如图9.2.3d、e所示。

（三）外伸部分截面的内力影响线

绘制截面K的剪力和弯矩影响线，如图9.2.4a所示。为计算方便，改取K点为坐标原点，并规定横坐标x以向右为正。当P=1在K点以左时，取截面K以右部分为隔离体，隔离体上没有任何荷载，显然V_K和M_K均等于零，故该两影响线在DK部分均与基线重合，当P=1在K点以右时，仍取截面K以右部分为隔离体，可得

V_K=1，M_K=-x

据以上两式，即可作出KE部分的V_K和M_K影响线，如图9.2.4b、c所示。

对于支座处截面的剪力影响线，我们需分支座左边与支座右边两个截面来分别讨论。

因为这两个截面是分别属于外伸和跨中部分的。例如，支座B右截面的剪力V_B右的影响线，可由V_K的影响线使截面K趋于支座B的右截面而得到如图9.2.4d所示；对于左截面的剪力V_B左的影响线，则可由V_C的影响线（图9.2.3d）使截面C趋于支座B的左截面而得到，如图9.2.4e所示。

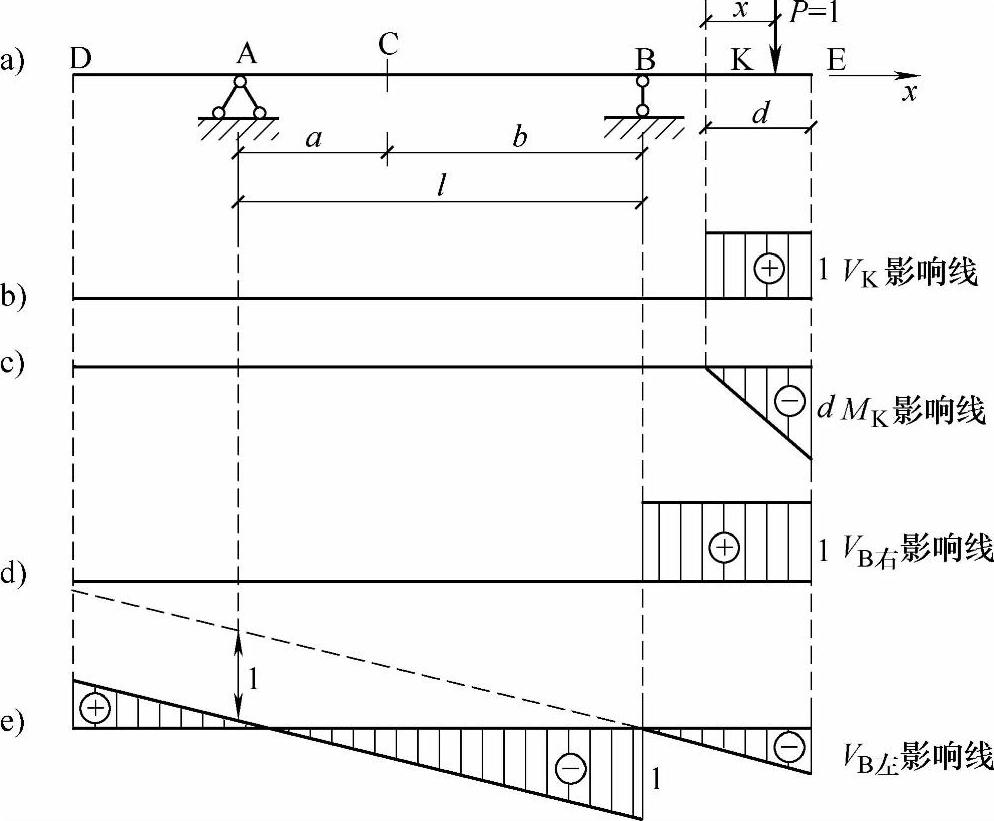
图 9.2.4

由上可以看出，静定梁的影响线均是由直线段组成的。