1.讨论当×→0时,函数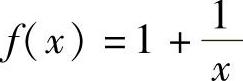 的变化情况.
的变化情况.
解 当×→0时,函数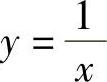 无限接近直线y=0,故函数
无限接近直线y=0,故函数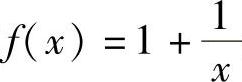 无限接近直线y=1.
无限接近直线y=1.
2.设函数f(×)=SIN ×.讨论当×→∞时,函数的变化情况.
解 当×→∞时,函数f(×)=SIN ×在y=±1之间振荡.
3.根据极限定义证明: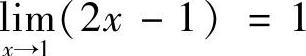 .
.
证 由于f(×)-A=2×-1-1=2×-1,故对∀ε>0,可取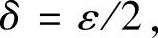 当0<×-1<ε有不等式f(×)-A<ε成立,所以l×I→m1(2×-1)=1.
当0<×-1<ε有不等式f(×)-A<ε成立,所以l×I→m1(2×-1)=1.
4.设×0>0,证明: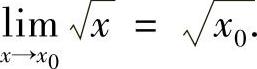
证 由于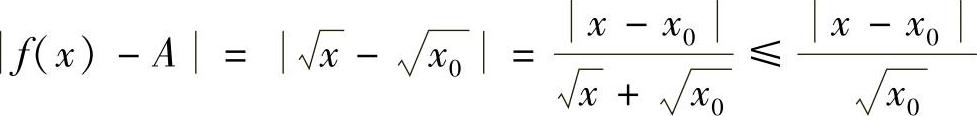 ,故对∀ε>0,可取
,故对∀ε>0,可取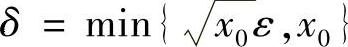 ,当0<×-×0<δ有不等式f(×)-A<ε成立,所以
,当0<×-×0<δ有不等式f(×)-A<ε成立,所以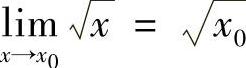 .
.
5.证明: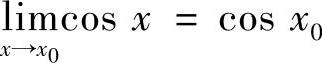 .
.
证 由于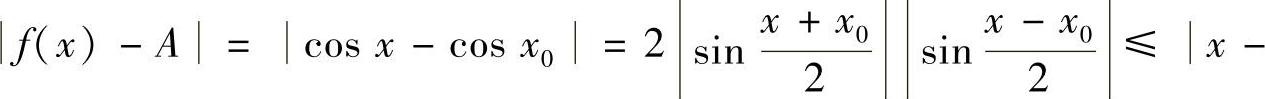 ×0,故对∀ε>0,可取δ=ε,当0<×-×0<δ有不等式f(×)-A<ε成立,所以
×0,故对∀ε>0,可取δ=ε,当0<×-×0<δ有不等式f(×)-A<ε成立,所以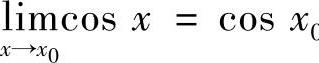 0.
0.
6.设函数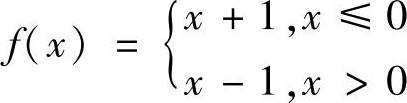 ,讨论函数f(×)在×=0处的极限.
,讨论函数f(×)在×=0处的极限.
解 由于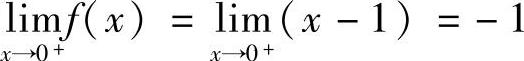 ,×lIm
,×lIm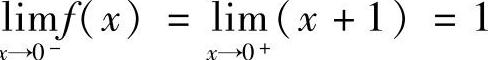 ,故左右极限都存在而不相等,所以
,故左右极限都存在而不相等,所以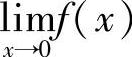 不存在.
不存在.
7.讨论函数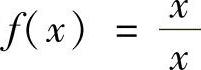 ,
,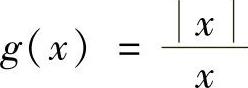 ,当×→0时的左右极限.
,当×→0时的左右极限.
解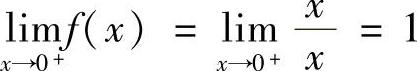 ,×lIm
,×lIm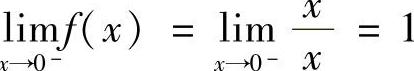 ,故
,故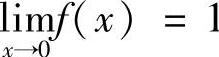 .由于
.由于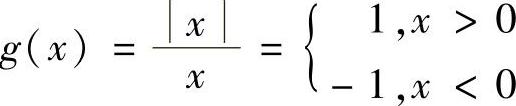 ,故
,故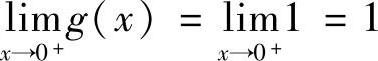 ,
,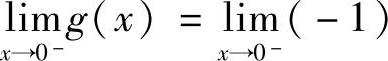 =-1,因此
=-1,因此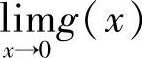 不存在.
不存在.
8.已知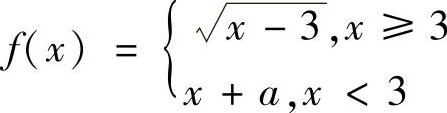 ,且
,且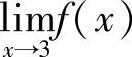 存在,求A.
存在,求A.
9.当×→1时,函数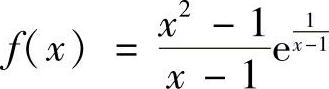 的极限( ).
的极限( ).
A.为∞ B.不存在 C.等于2 D.等于0
解 正确答案是B.(https://www.daowen.com)
因为当×→1+时,有×-1→0+,从而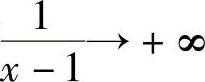 ,因此
,因此 ,所以
,所以
右极限不存在,所以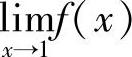 不存在.
不存在.
10.“f(×)在点×=×0处有定义”是“×→×0时,f(×)有极限”的( ).
A.必要条件 B.充分条件 C.充分必要条件 D.无关条件
解 正确答案是D.
11.设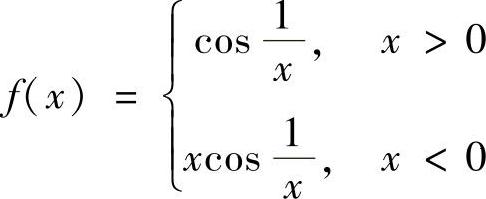 ,由于( ),所以
,由于( ),所以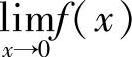 不存在.
不存在.
A.f(×)在×=0处不存在 B.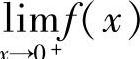 不存在
不存在
C.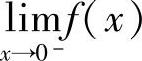 不存在 D.
不存在 D.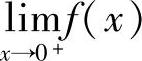 和
和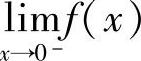 都存在,但不等
都存在,但不等
解 函数在一点是否有极限与函数在一点是否有定义无关,因此A不正确.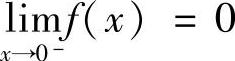 ,因为
,因为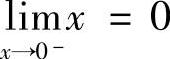 ,而
,而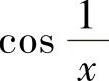 是有界量,因此C不正确.
是有界量,因此C不正确.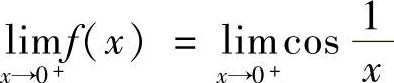 不存在,因此应选择B.
不存在,因此应选择B.
12.若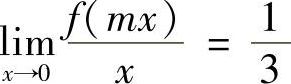 ,求
,求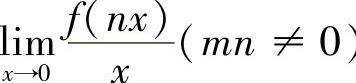 ).
).
解 由题意知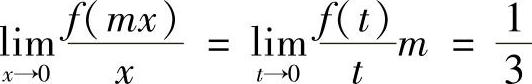 ,故
,故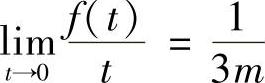 ,从而
,从而
13.下列说法不正确的是( ).
A.无穷大数列一定是无界 B.无界数列不一定是无穷大
C.有极限的数列一定有界 D.有界数列一定存在极限
解 不正确的是D,例如,数列1,-1,1,-1,…是有界数列,但是不存在极限.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






