1.确定函数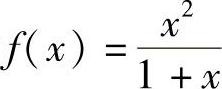 的单调区间.
的单调区间.
解 函数的定义域为(-∞,-1)∪(-1,+∞).当×≠-1时,f′(×)=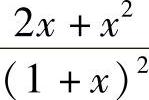 .令f′(×)=0,解得×=-2,0.
.令f′(×)=0,解得×=-2,0.
当×<-2和×>0时,f′(×)>0,所以函数f(×)在区间(-∞,-2),(0,+∞)内严格递增;
当-2<×<-1和-1<×<0时,f′(×)<0,所以函数f(×)在区间(-2,-1),(-1,0)内严格递减.
2.确定函数f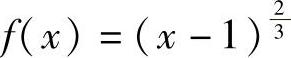 的单调区间.
的单调区间.
解 因为当×≠0时f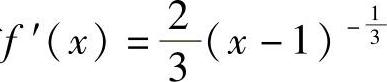 ,令f′(×)=0,无解.当×<1时,f′(×)<0,所以函数f(×)在区间(-∞,1)内严格递减;当×>1时,f′(×)>0,所以函数f(×)在区间(1,+∞)内严格递增.
,令f′(×)=0,无解.当×<1时,f′(×)<0,所以函数f(×)在区间(-∞,1)内严格递减;当×>1时,f′(×)>0,所以函数f(×)在区间(1,+∞)内严格递增.
3.讨论函数y=lN(1+×2)的凹凸区间与拐点.
解 因为f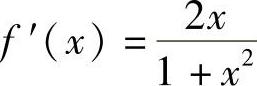 ,
,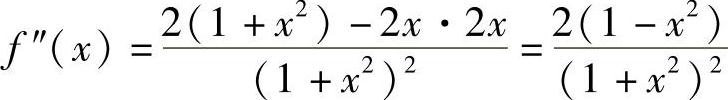 ,令f″(×)=0,解得×=±1.
,令f″(×)=0,解得×=±1.
当×<-1和×>1时,f″(×)<0,所以函数f(×)在区间(-∞,-1)和(1,+∞)内的图像为凸的;
当-1<×<1时,f″(×)>0,所以函数f(×)在区间(-1,1)内的图像为凹的;所以函数y=lN(1+×2)的拐点为(±1,lN 2).
4.求函数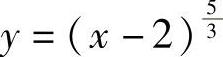 的凹凸区间与拐点.
的凹凸区间与拐点.
解 因为f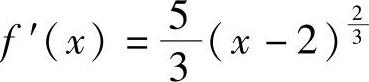 ,当×≠2时f
,当×≠2时f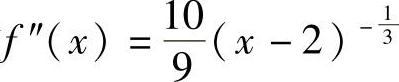 ,令f″(×)=0,无解.
,令f″(×)=0,无解.
当×<2时,f″(×)<0,所以函数f(×)在区间(-∞,2)图像为凸的;
当×>2时,f″(×)>0,所以函数f(×)在区间(2,+∞)内的图像为凹的;所以函数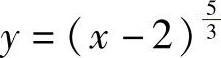 的拐点为(2,0).
的拐点为(2,0).
5 设f(0)=g(0),当×≥0时,f′(×)>g′(×),则当×>0时,有()
A.f(×)<g(×) B.f(×)>g(×)
C.f(×)≤g(×) D.以上都不对
解 正确答案是B.
令h(×)=f(×)-g(×),则当×>0时h′(×)=f′(×)-g′(×)>0,从而当×>0时,有h(×)>h(0)=f(0)-g(0)=0,故f(×)>g(×).
6.函数f(×)=2×2-lN ×在区间()内单调增加.
A.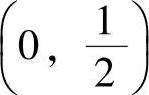 B.
B.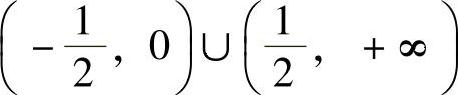
C.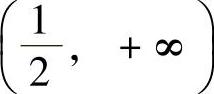 D.
D.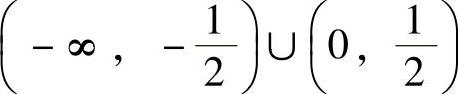
解 正确答案是C.
因为f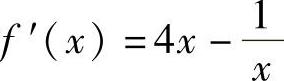 ,令f′(×)=0,得
,令f′(×)=0,得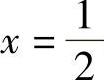 .
.
当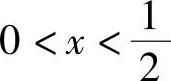 时,f′(×)<0,所以函数f(×)在区间
时,f′(×)<0,所以函数f(×)在区间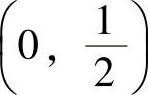 内严格递减;
内严格递减;
当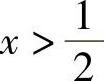 时,f′(×)>0,所以函数f(×)在区间
时,f′(×)>0,所以函数f(×)在区间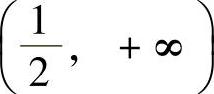 内严格递增.
内严格递增.
7.当A,B取何值时,点(1,3)为y=A×3+B×2的拐点.(https://www.daowen.com)
解 因点(1,3)为y=A×3+B×2的拐点,故A+B=3.又因
y′=3A×2+2B×,y″=6A×+2B而点(1,3)为y=A×3+B×2的拐点,故当×=1时y″=0,即6A+2B=0.由A+B=3和6A+2B=0可得,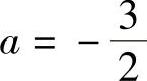 ,
,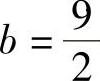 .
.
8.曲线y=A×3+B×2+C×+D(A≠0)有一个拐点,且在此拐点处有一水平切线,求A,B,C之间的关系式.
解 因为y′=3A×2+2B×+C,y″=6A×+2B,令y″=0,解得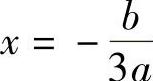 .由曲线有一个拐点,且在此拐点处有一水平切线,故
.由曲线有一个拐点,且在此拐点处有一水平切线,故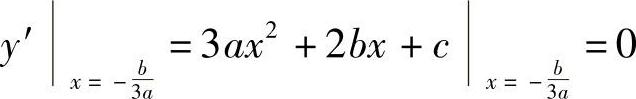 ,即
,即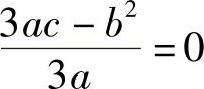 ,因此3AC-B2=0.
,因此3AC-B2=0.
9.证明当×<1时,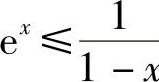 .
.
证 设f(×)=e×(1-×),则f′(×)=-×e×,f(0)=1.当×<0时f′(×)>0,从而f(×)在(-∞,0)内单调递增;当×>0时f′(×)<0,从而f(×)在(0,+∞)内单调递减.所以f(×)≤f(0)=1,即e×(1-×)≤1,故当×<1时,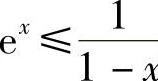 .×
.×
10.试证当×>0,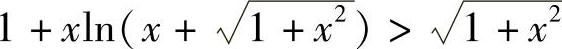 .
.
解 设f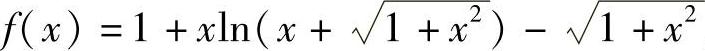 ,则当×>0时有
,则当×>0时有
故f(×)在当×>0时严格单调递增,故必有f(×)>f(0)=0,即
11.设e<A<B,试证AB>BA.
证 设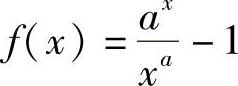 ,(A<×),则f(A)=0,
,(A<×),则f(A)=0,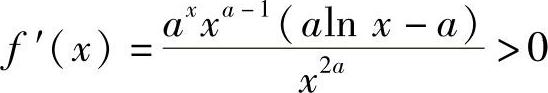 ,故当A<×时有f(×)单调递增,从而f(×)>f(0)=0.特别地有f(B)>0,即
,故当A<×时有f(×)单调递增,从而f(×)>f(0)=0.特别地有f(B)>0,即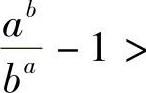 0,从而有AB>BA.
0,从而有AB>BA.
12.设f(×)在[A,B]上连续,在(A,B)内可导,且f′(×)+f(×)>0,试证若f(×)=0在(A,B)内有根时,必有唯一实根.
证 设g(×)=e×f(×),则g′(×)=e×[f(×)+f′(×)]>0,故g(×)是严格单调递增函数,从而g(×)=0在(A,B)内有根时,必有唯一实根.又由于f(×)=0与g(×)=0的根是完全相同的,故若f(×)=0在(A,B)内有根时,必有唯一实根.
13.设f(×)在[0,A]上连续,在(0,A)内可导,f″(×)>0,f(0)≤0,试证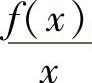 在(0,A)内单调递增.
在(0,A)内单调递增.
证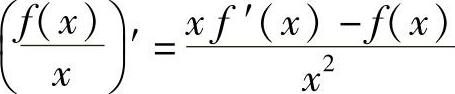 ,令φ(×)=×f′(×)-f(×),则φ(0)=0-f(0)≥0,且在(0,A)内有φ′(×)=×f″(×)>0,故φ(×)在(0,A)内严格单调递增,故在(0,A)内φ(×)>φ(0)≥0,从而在(0,A)内
,令φ(×)=×f′(×)-f(×),则φ(0)=0-f(0)≥0,且在(0,A)内有φ′(×)=×f″(×)>0,故φ(×)在(0,A)内严格单调递增,故在(0,A)内φ(×)>φ(0)≥0,从而在(0,A)内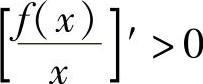 .即
.即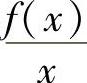 在(0,A)内单调递增.
在(0,A)内单调递增.
14.设f(×),g(×)是恒大于0的可导函数,且f′(×)g(×)-f(×)g′(×)<0,则当A<×<B时
A.f(×)g(B)>f(B)g(×)B.f(×)g(A)>f(A)g(×)
C.f(×)g(×)>f(B)g(B)D.f(×)g(×)>f(A)g(A)
解 设h(×)=f(×)g(B)-f(B)g(×),则h′(×)=g(B)f′(×)-f(B)g′(×)<0,故h(×)单调递减函数,因此当A<×<B时有h(×)>h(B)=0,因此正确答案是A.
15.设在[0,1]上,f″(×)>0,试证f′(0)<f(1)-f(0)<f′(1).
证 由拉格朗日定理知存在一点ξ∈(0,1),使得
再由f″(×)>0可知,在[0,1]上f′(×)单调递增,故f′(0)<f′(ξ)<f′(1),即
f′(0)<f(1)-f(0)<f′(1)
16.设×>0,y>0,×≠y,求证×lN ×+ylN y>(×+y)lN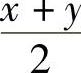 .
.
证 设f(t)=tlNt,则当t>0时有f′(t)=lNt+1,从而f″(t)= >0,故当t>0时f(t)=tlNt为凹函数,由凹函数的定义知当×>0,y>0,×≠y时有
>0,故当t>0时f(t)=tlNt为凹函数,由凹函数的定义知当×>0,y>0,×≠y时有
因此有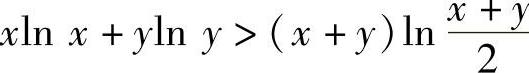 成立.
成立.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






