1.设y=6×3+3×2+×+5,求y‴,y(4).
解y‴=(6×3+3×2+×+5)‴=(6×3)‴=6·3·2·1=36,y(4)=0.
2.设f(×)=×e×2,求f″(×).
解f′(×)=e×2+×·e×2·2×=e×2(1+2×2)f″(×)=[e×2(1+2×2)]′=e×2·2×(1+2×2)+e×2·4×=2×e×2(2×2+3)
3.求下列函数的N阶导数.
(1)y=SIN A× (2)y=eB× (3)y=lN(1+×)
解 (1)
(2)y′=BeB×,y″=B2 eB×,…,y(N)=BN eB×
(3) ,
, ,
,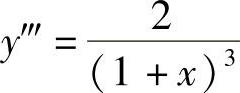 ,…,
,…,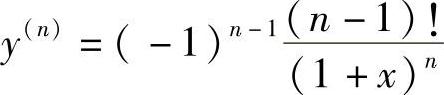
4.设函数y=y(×)是由方程ey+×y=e确定,求y′(0),y″(0).
解 方程两边对×求导数,有eyy′+y+×y′=0,从而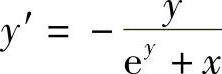 ,因此
,因此 式
式 两端对×求导数,有
两端对×求导数,有
从而 .
.
5.设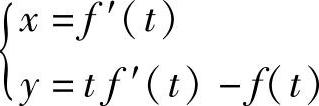 ,且f″(t)≠0,求
,且f″(t)≠0,求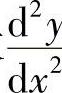 .
.
解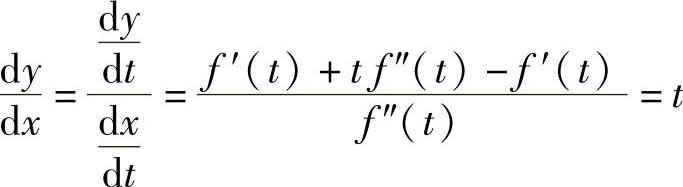
6.若y=e f(×),求y″;又若y=×2 lN×,求y″.
解 若y=e f(×),则y′=e f(×)·f′(×),从而y″=e f(×)·[f′(×)]2+e f(×)f″(×)
若y=×2 lN×,则y′=2×·lN×+×,则y″=2lN×+2+1=2lN×+3
7.设f(×)=SIN ×+CoS ×,求f(27)(π)的值.
解 (https://www.daowen.com)
(https://www.daowen.com)
8.设y=×lNf(-×),f(×)二阶可导,求y″.
解 ,因此
,因此
9.设f(×)=×e-×,求f(N)(×).
解f′(×)=e-×-×e-×
f″(×)=-e-×-(e-×-×e-×)=-2e-×+×e-×
f‴(×)=2e-×+e-×-×e-×=3e-×-×e-×
…
f(N)(×)=(-1)N-1 e-×N+(-1)N×e-×=(-1)N-1 e-×(N-×)
10.设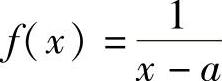 ,求f(N)(×).
,求f(N)(×).
解 易得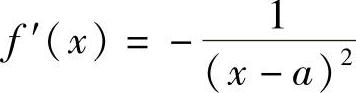
故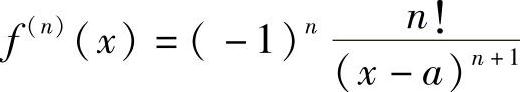 .
.
11.设 ,求y(N)(2≤N).
,求y(N)(2≤N).
解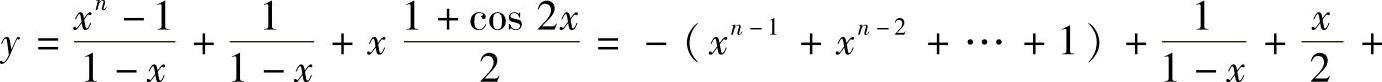
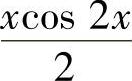 ,故
,故
12.设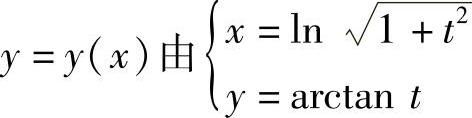 所确定,求
所确定,求 .
.
解 ,因此
,因此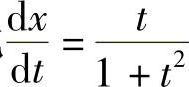 ,从而
,从而 .故
.故
13.试从 导出:(1)
导出:(1) ;(2)
;(2)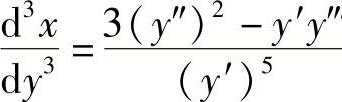 ‴.
‴.
证 (1)
(2)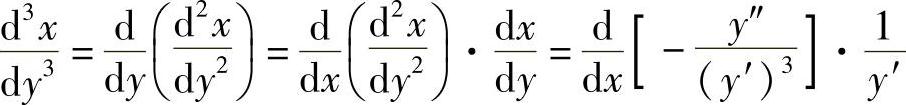
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







