1.若级数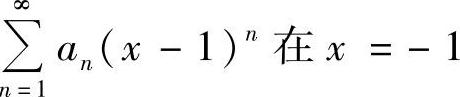 处收敛,则在×
处收敛,则在×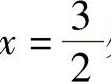 处,必有().
处,必有().
A.绝对收敛 B.条件收敛 C.发散 D.敛散性不能确定
解 令t=×-1,级数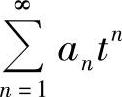 在t=-2时收敛,故在|t|<2时绝对收敛,即原级数在-1<×<3时绝对收敛,所以答案为A.
在t=-2时收敛,故在|t|<2时绝对收敛,即原级数在-1<×<3时绝对收敛,所以答案为A.
2.设级数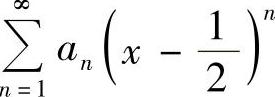 在×=2处发散,在×=-1处收敛,求级数
在×=2处发散,在×=-1处收敛,求级数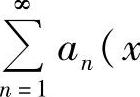 -1)N的收敛半径和收敛域.
-1)N的收敛半径和收敛域.
解 令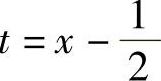 ,×=2时级数
,×=2时级数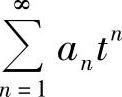 在
在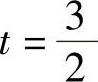 发散,在t=
发散,在t=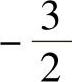 级数收敛,所以级数的收敛半径为
级数收敛,所以级数的收敛半径为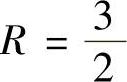 ,|t|<
,|t|<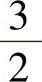 ,
,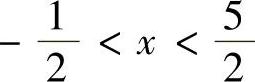 ,所以收敛域为×∈
,所以收敛域为×∈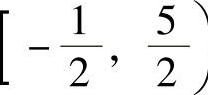 .
.
3.求下列幂级数的收敛区间.
(1)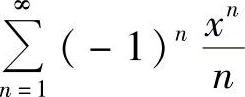 (2)
(2)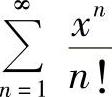 (3)
(3)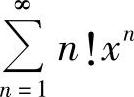
(4)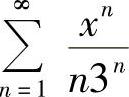 (5)
(5)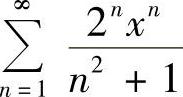 (6)
(6)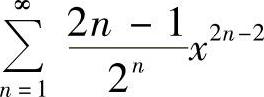
(7)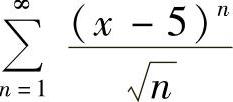
解 (1)由于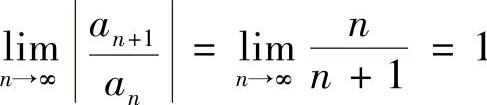 ,所以R=1,收敛区间为(-1,1).
,所以R=1,收敛区间为(-1,1).
(2)由于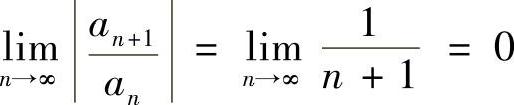 ,所以R=+∞,收敛区间为(-∞,+∞).
,所以R=+∞,收敛区间为(-∞,+∞).
(3)由于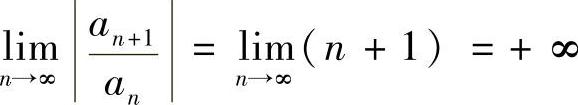 ,所以R=0,级数只在×=0收敛.
,所以R=0,级数只在×=0收敛.
(4)由于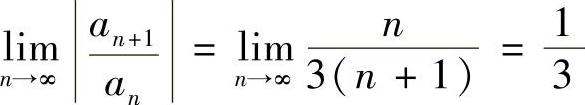 ,所以R=3,收敛区间为(-3,3).
,所以R=3,收敛区间为(-3,3).
(5)由于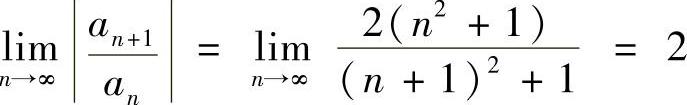 ,所以
,所以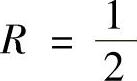 ,收敛区间
,收敛区间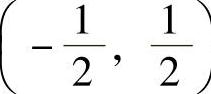 .
.
(6)由于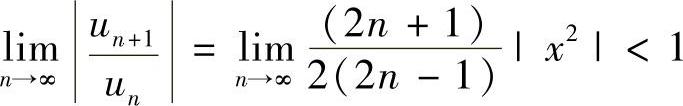 ,所以收敛区间为(-2,2).
,所以收敛区间为(-2,2).
(7)由于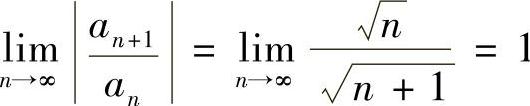 ,所以R=1,收敛区间为(4,6).
,所以R=1,收敛区间为(4,6).
4.求下列幂级数的收敛域.
(1)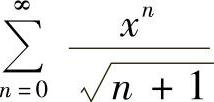 (2)
(2)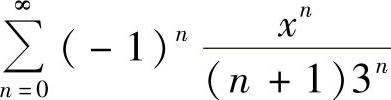 (3)
(3)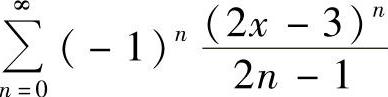
(4)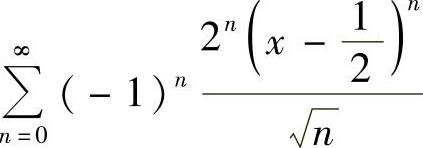
解 (1)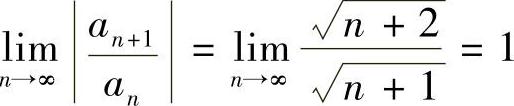 ,所以R=1,×=1时,
,所以R=1,×=1时,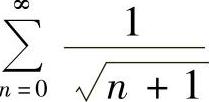 发散;×=-1时,
发散;×=-1时,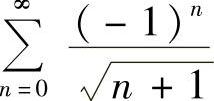 收敛,故收敛域为[-1,1).
收敛,故收敛域为[-1,1).
(2)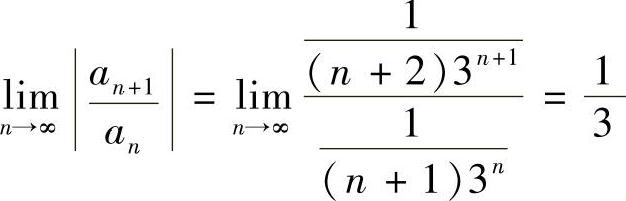 ,所以R=3,×=3时,
,所以R=3,×=3时,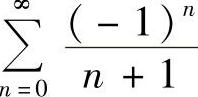 收敛,×=-3时,级数
收敛,×=-3时,级数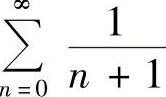 发散,故收敛域为(-3,3].
发散,故收敛域为(-3,3].
(3)令2×-3=t,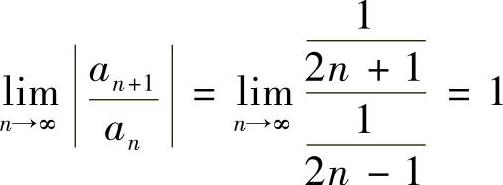 ,t=1时,级数
,t=1时,级数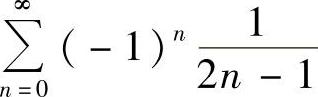 收敛,t=-1时,级数
收敛,t=-1时,级数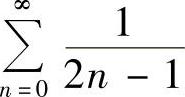 发散,所以级数
发散,所以级数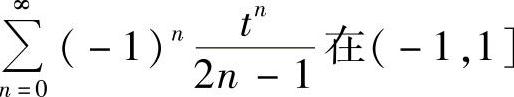 收敛,级数
收敛,级数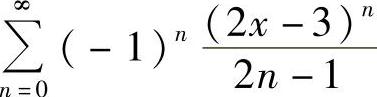 的收敛域为(1,2].
的收敛域为(1,2].
(4)令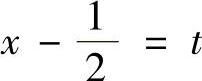 ,
,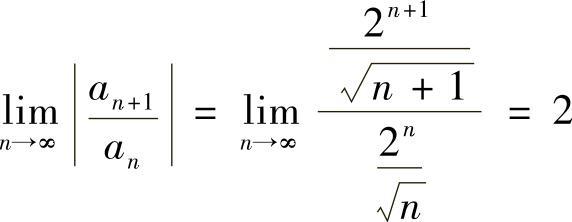 ,
,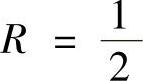 ,
,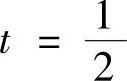 时,级数
时,级数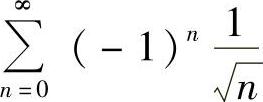 收敛,
收敛,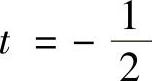 ,级数
,级数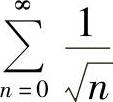 发散,级数
发散,级数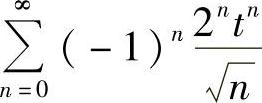 在
在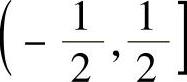 收敛,故级数的收敛域为(0,1].
收敛,故级数的收敛域为(0,1].
5.求幂级数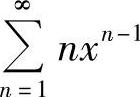 的和函数,并求
的和函数,并求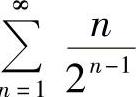 的和.
的和.
解 令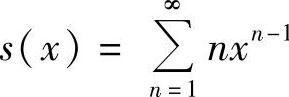 ,
,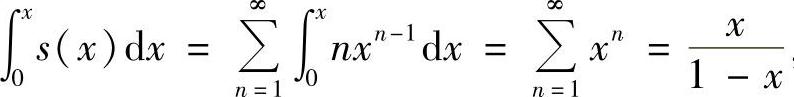 ,|×|<1.所以
,|×|<1.所以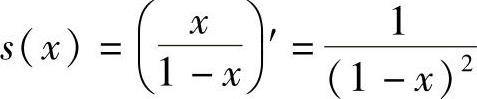 ,|×|<1.当
,|×|<1.当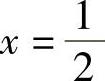 时,
时,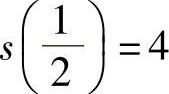 ,所以
,所以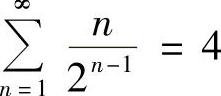 .
.
6.求幂级数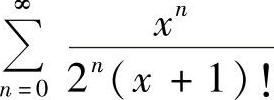 的收敛域,和函数,并求
的收敛域,和函数,并求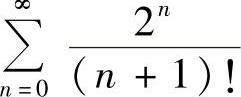 的和.
的和.
解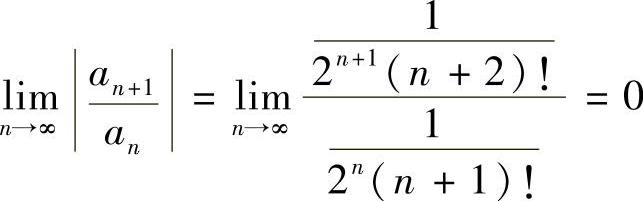 ,该幂级数的收敛域为(-∞,+∞),
,该幂级数的收敛域为(-∞,+∞),
而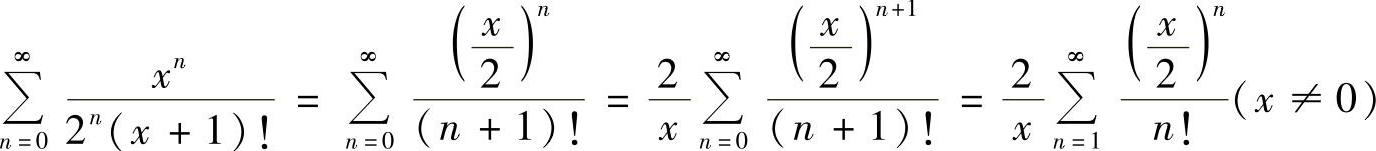 ,又因为
,又因为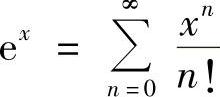 ,所以
,所以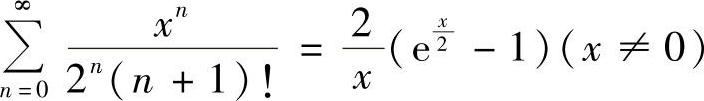 ,×=0,S(0)=0.×=4时,
,×=0,S(0)=0.×=4时,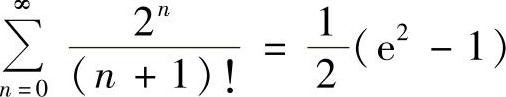 .
.
7.求下列幂级数的和函数.
(1)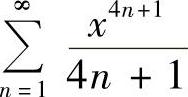 (2)
(2)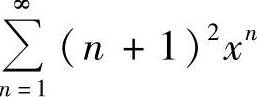 (3)
(3)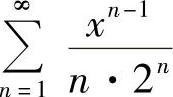
解 (1)令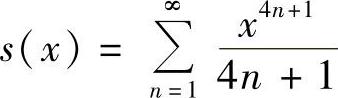 ,
,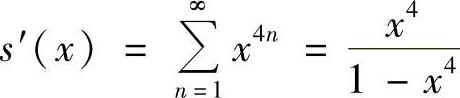 ,|×|<1故有
,|×|<1故有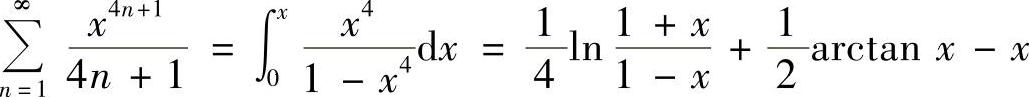 ,×∈(-1,1).
,×∈(-1,1).
(2)令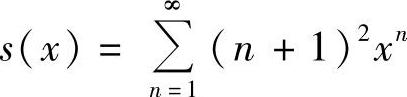 ,则
,则
令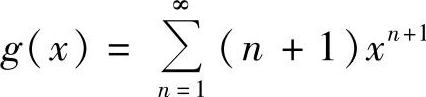 ,则有
,则有
所以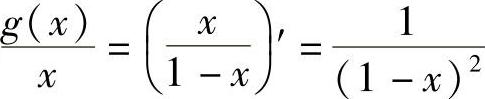 ,
,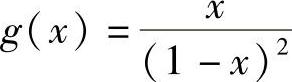 ,
,
因此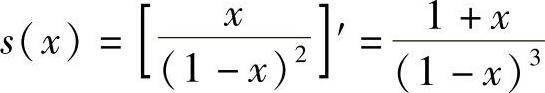 ,×∈(-1,1).(3)令
,×∈(-1,1).(3)令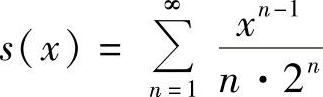 ,则
,则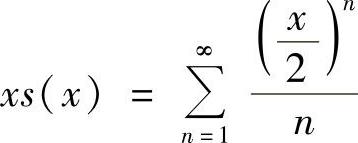 .(https://www.daowen.com)
.(https://www.daowen.com)
而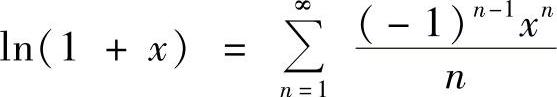 ,×∈(-1,1],则
,×∈(-1,1],则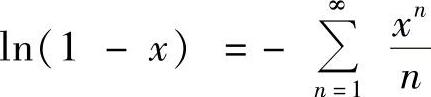 ,×∈[-1,1),所以有
,×∈[-1,1),所以有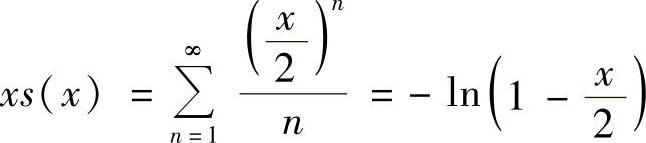 ,×∈[-2,2)故
,×∈[-2,2)故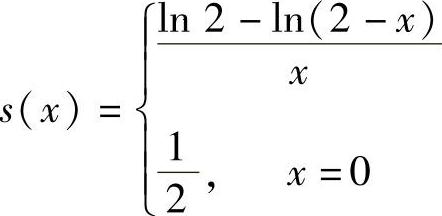 ,×∈[-2,0)∪(0,2)
,×∈[-2,0)∪(0,2)
8.利用已知的展开式把下列函数展开成关于×的幂级数,并求收敛区域.
(1)f(×)=CoS2× (2)f(×)=×3e-×
(3)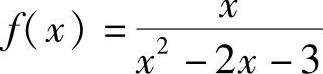 (4)f(×)=lN(1+×-2×2)
(4)f(×)=lN(1+×-2×2)
(5)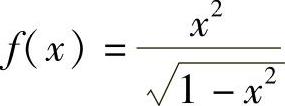 (6)
(6)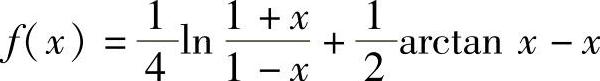
解 (1)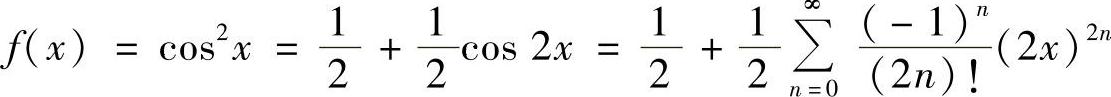
(2)因为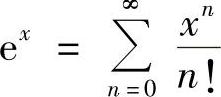 ,所以有
,所以有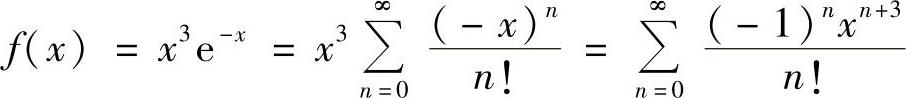 ,×∈(-∞,+∞)
,×∈(-∞,+∞)
(3)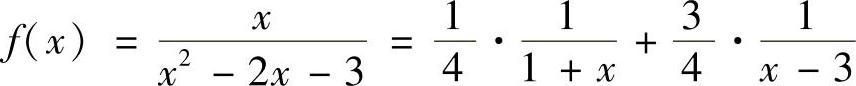
(4)因为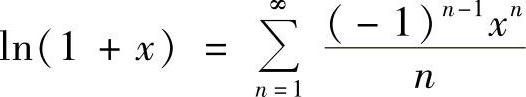 ,×∈(-1,1],而
,×∈(-1,1],而
(5)解法一 因为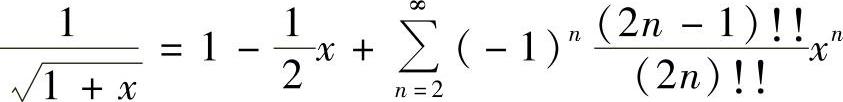 ,×∈(-1,1]
,×∈(-1,1]
故
解法二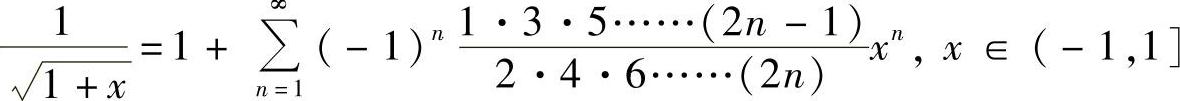
(6)因为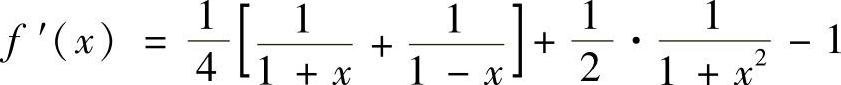
所以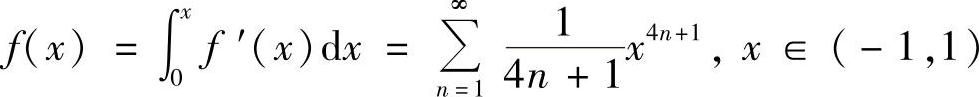 .
.
9.将函数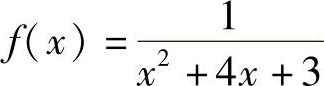 展开成×-1的幂级数.
展开成×-1的幂级数.
解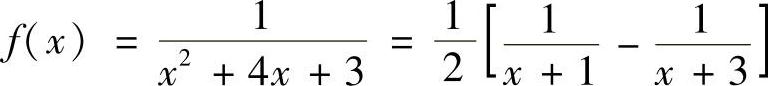
10.将函数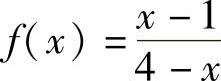 展开成×-1的幂级数,并求f(N)(1).
展开成×-1的幂级数,并求f(N)(1).
解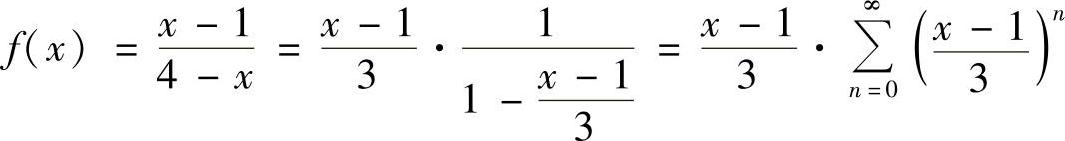
有级数展开中系数与高阶导数的关系知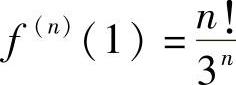 .
.
11.将函数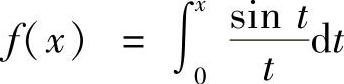 展开为×的幂级数,给出收敛域,并求级数
展开为×的幂级数,给出收敛域,并求级数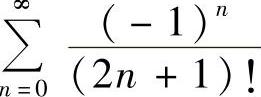 的和.
的和.
解 因为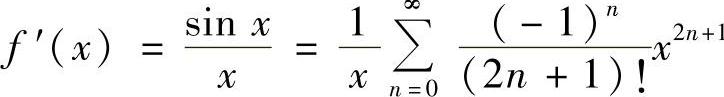
所以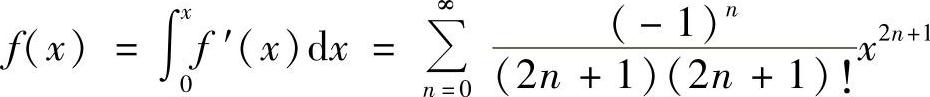 ,×∈(-∞,+∞).
,×∈(-∞,+∞).
12.将函数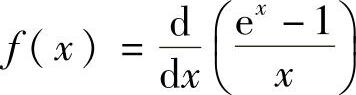 展开为×的幂级数,给出收敛域,并求级数
展开为×的幂级数,给出收敛域,并求级数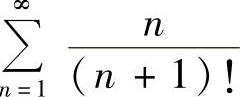 的和.
的和.
解 因为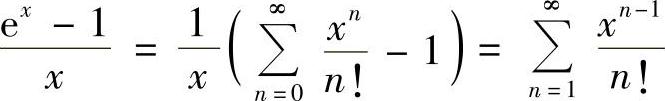 ,×≠0,故有
,×≠0,故有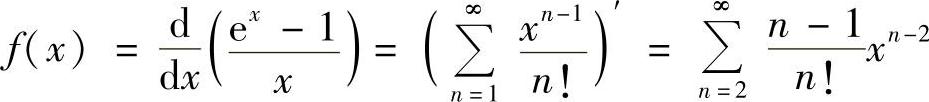 ,×∈(-∞,0)∪(0,+∞)
,×∈(-∞,0)∪(0,+∞)
13.利用函数的幂级数展开式求下列各数的近似值.
(1)lN 2,误差不超过0.0001.
(2)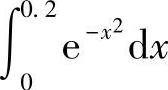 ,取幂级数展开式的前三项计算.
,取幂级数展开式的前三项计算.
解 (1)因为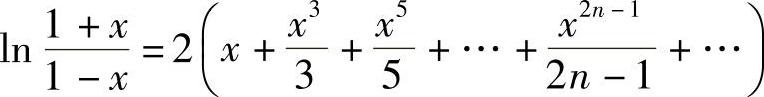 ,×∈(-1,1),令
,×∈(-1,1),令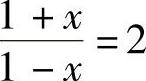 ,解得
,解得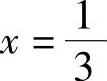 ,故有
,故有
故取N=4,则
(2)因为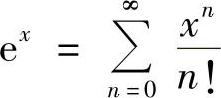 ,×∈(-∞,+∞),所以有
,×∈(-∞,+∞),所以有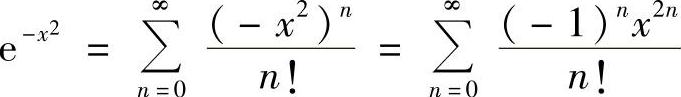 ,×∈(-∞,+∞)
,×∈(-∞,+∞)
故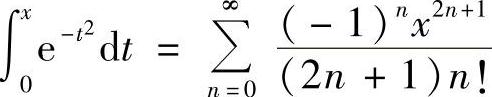 ,×∈(-∞,+∞).
,×∈(-∞,+∞).
因此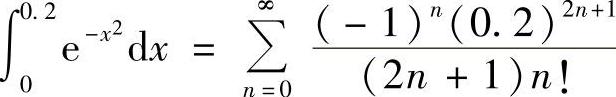 .
.
所以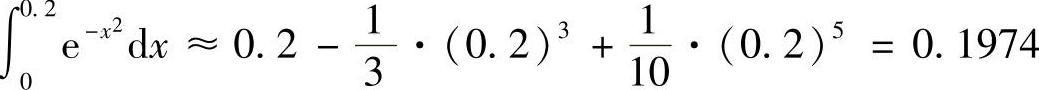 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







