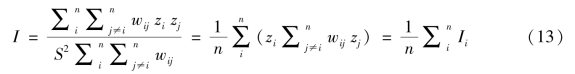(二)模型选择
1.动态因子分析法
本研究采用动态因子法来综合测度长江中游地区28个主要地级市的城市创新能力与新型城镇化水平。
动态因子分析法全面考虑了变量、时间和样本三个要素,假定了三维阵列运算模型:
公式(1)中,i代表第i个样本;j代表第j个指标;t指代不同的时间
公式(1)是动态因子分析法的主体模型,其中,
·表示第j个变量的整体均值;
表示不同的样本结构伴随着时间的改变而造成的影响;
是整体的平均动态效应;
代表了动态差异导致的影响,也就是某一样本与时间产生的相互影响。公式(2)中的总变异可以进一步细分为另外两部分:
公式(2)中,*SI表示样本的静态结构矩阵;ST是不同时期的平均离差矩阵;*ST是运用线性回归LS模型产生的不同时间的变异;SIT反映了全部样本整体的均值水平波动与某一样本波动导致的动态差异矩阵。
详细的计算过程为:
①首先对所有的指标数据进行标准无量纲化处理
对于体系中的正向指标,
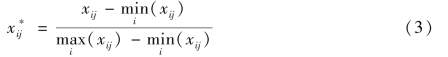
对于体系中的逆向指标,
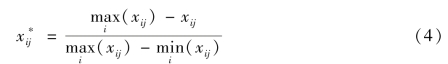
②依据每一年的协方差矩阵S(t),求解得到能够综合体现数据整体结构差异和动态差异影响的平均协方差矩阵ST.
③求取ST的特征值和它的不同公因子的方差贡献率
④发现当中的公因子,并据此构建原始的因子载荷矩阵
⑤求解样本的静态得分矩阵
其中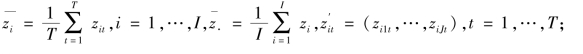
⑥计算每年各个样本的动态得分
其中
2.耦合协调模型
基于前人研究的基础上,本研究构建包含创新能力与新型城镇化水平两系统的耦合协调度模型,具体步骤如下:
(1)指标的标准化
为了保证耦合协调模型后续计算的正常进行,将上述两个系统的得分分别进行标准化处理,公式为:
式中,Xij代表第i个市域单元的第j年 的综合指数得分,min(Xij)和max( Xij )代表各综合得分数据中的最小值和最大值,标准化处理后的Uij取值范围是[0,1]。
(2)建立创新能力和新型城镇化水平两个系统之间的耦合度模型,公式为:
式中,C代表耦合度;U1、U2分别代表两大系统的综合发展指数。
耦合度C的取值范围是[0,1]。越趋近于1,表示二者耦合的程度越高,耦合度越趋近于0,表示二者的发展关联性越低,呈现无序的发展趋势。C越大,表明城市创新能力与城市化水平之间的良性共振耦合性越好。
(3)建立创新能力和新型城镇化水平的耦合协调度模型
耦合协调度模型通过构建一个定量的“协调度”指标来衡量两个系统之间或是单独的系统内部各要素间的协调状况,依据该指标可以判断它们之间的耦合性质与阶段。具体公式如下:
上述公式中,T代表城市创新能力与城市化两系统的综合协调指数;α、β分别表示二者重要程度的未知待定系数,本研究认为城市创新能力与新型城镇化水平同等重要,所以α和β的值都取0.5;D代表耦合协调度,取值范围是[0,1]。D的取值越接近1,耦合协调度越高,二者发展协调;D的取值越接近0,耦合协调度越低,说明发展失调。
3.探索性空间数据分析法
在同一区域内,城市的发展各不相同,且各城市并不是独立、随机发展的,城市间存在各方面的关联。探索性空间数据分析法,是一种将图表类信息与统计学方法融合在一起的将空间信息的特性进行深入鉴别分析的“数据驱动”方法。该方法在处理研究样本的总体空间格局差异性和关联性上十分理想。在地理学上会出现一种现象,即邻近的区域或城市之间在某些性质的体现上会呈现出某种联系,而ESDA法就是为了测度不同单元之间由于地理位置的邻近而导致的这种联系的相关性的强弱。具体而言,ESDA法就是把想要观测的目标变量与观测单元的地理位置结合在一起进行探究,比较这一观测变量值与其空间位置的关联相似性。
(1)全局空间自相关
用以反映研究样本地理邻近的研究单元的属性的类似性,用于检验总体的空间关联与差异性。一般采取Global Moran's I指数衡量,具体公式为:
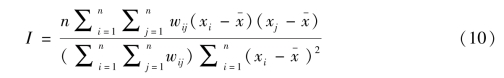
公式(10)中,n表示研究样本内的区域数量;其中
与xj分别为地区i和j的属性值;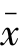
表示这些属性的一个均值;wij是空间权重矩阵。当i地区与j地区相邻时,wij=1;不相邻时,wij=0。
上述公式得出的Moran's I值的范围是[-1,1],正值表示研究区域存在空间正相关性,负值代表研究区域存在空间负相关性,而0值则表示无相关性,Moran's I值与0相隔越远,表示这种相关性越强。
构建零假设为:待观测变量值在空间上无相关性。然后对其进行检验,统计量z值是标准化之后的Moran's I值。
(2)局部空间自相关
上述的全局Moran's I值是从总体上判断全部观测单元的空间关联性,这种方法也会存在部分弊端,如无法判断在一个具有全局空间正相关的研究区域中是否所有研究单元均存在局部正相关。这是因为全局空间自相关假设空间一直是平稳不变的,然而现实生活中,由于各种因素的存在,空间一般很难保持长久的稳定性,因此该假设也就不复成立。在这种情况下,我们利用局部Moran's I值统计量来判别在区域内容的研究单元观测值因所处地理位置不同而呈现出的具有差异性的空间关联特征。一般采取LISA(Local Indicators of Spatial Association)分析与Moran散点图来衡量。
LISA指标用于度量样本区域与邻边区域的相关程度及显著性,该指标可以发现对整体影响较大的单元,具体的计算公式如下:
公式(12)中,zi与zj指代的是将观测值进一步标准化后得到的数值,wij则是把空间权重矩阵进行行标准化后的数值。全局Moran's I值和局部Moran's Ii二者间也存在一定的数量关系:
