1.确定下列函数的定义域.
(1)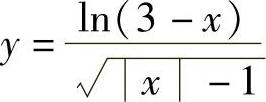
(2)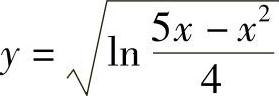
(3)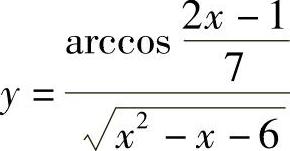
(4)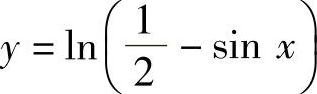
2.下列函数可以看成由哪些简单函数复合而成.
(1)y=(1+lN×)5
(2)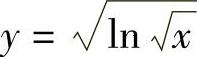
(3)y=ee-×2
(4)y=lN2ArCCoS×2
3.填空题.
(1)设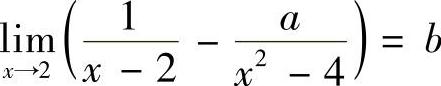 ,则AB=.
,则AB=.
(2)已知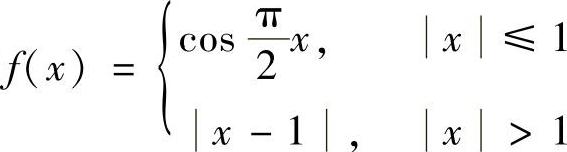 ,则×=为f(×)的第类间断点.
,则×=为f(×)的第类间断点.
(3)设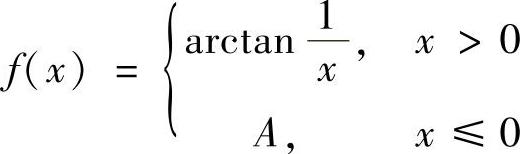 ,在×=0处连续,则A=.
,在×=0处连续,则A=.
(4)已知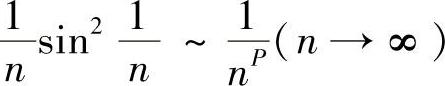 ,则常数P=.
,则常数P=.
(5)设函数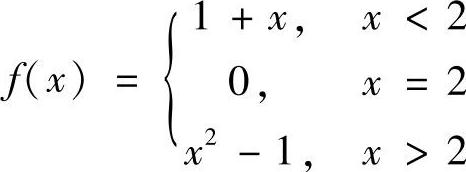 ,则l×I→m1f[f(×)]=.
,则l×I→m1f[f(×)]=.
(6)设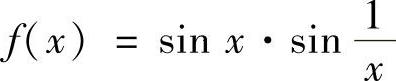 ,则×=0是f(×)的第类间断点.
,则×=0是f(×)的第类间断点.
(7)若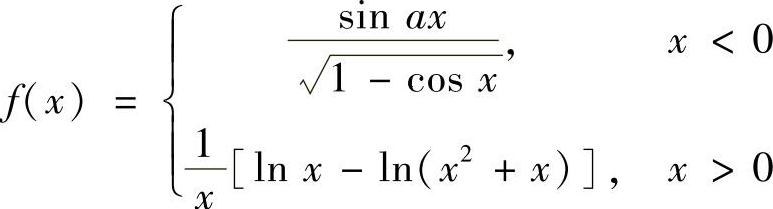 ,若极限
,若极限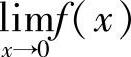 存在,则A=
存在,则A=
.
(8)设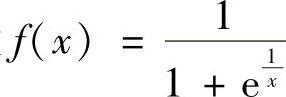 ,则
,则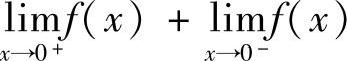 =.
=.
(9)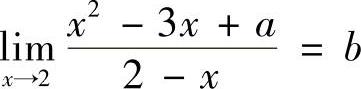 ,则A=,B=.
,则A=,B=.
(10)设f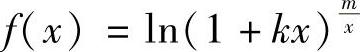 ,补充定义f(0)=可使其在×=0处连续.
,补充定义f(0)=可使其在×=0处连续.
4.选择题.
(1)下列函数中,( )不为初等函数.
A.y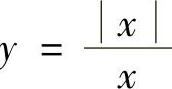 B.
B.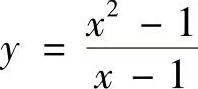
C.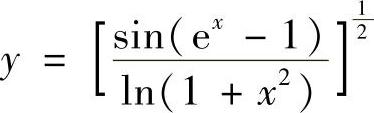 D.y=×
D.y=×
(2)下列函数中,( )为奇函数.
A.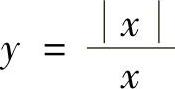 B.
B.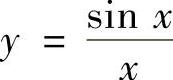
C.y=×2+CoS× D.y=f(×2)
(3)函数y=SIN×的周期为( ).
A.4π B.π
C.2π D.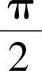
(4)“f(×)在×=A连续“是“f(×)在×=A连续”的( )条件.
A.必要非充分 B.充分非必要
C.充要 D.既非充分又非必要
(5)设f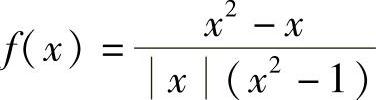 ,则下列结论错误的是( ).(https://www.daowen.com)
,则下列结论错误的是( ).(https://www.daowen.com)
A.×=1,×=0,×=-1为间断点 B.×=0为可去间断点
C.×=-1为无穷间断点 D.×=0为跳跃间断点
(6)函数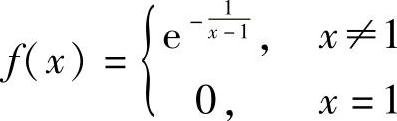 ,在×=1处( ).
,在×=1处( ).
A.右连续 B.左、右皆不连续 C.左连续 D.连续
(7)下列函数在定义域内不连续的是( ).
A.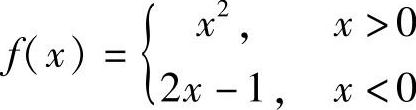 B.
B.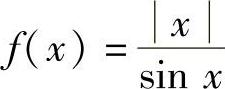 C.f
C.f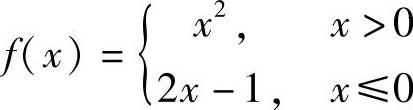 D.f(×)=1+SIN ×+SIN2×+…,
D.f(×)=1+SIN ×+SIN2×+…,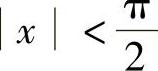
(8)若数列{yN}满足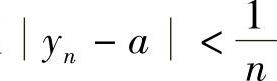 ,N=1,2,3,…,则当N→∞时,必有().
,N=1,2,3,…,则当N→∞时,必有().
A.yN是无穷小量 B.yN是无界变量 C.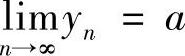 D.yN是无穷大量
D.yN是无穷大量
(9)下列函数中,()在点×=0补充定义可成为连续函数
A.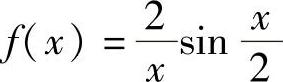 B.
B.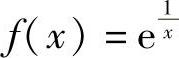 C.
C.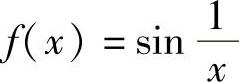 D.
D.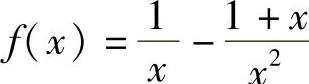
(10)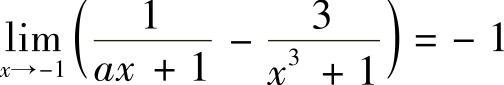 ,则A=( ).
,则A=( ).
A.1 B.-1 C.0 D.以上都不对
(11)若×→0时,2SIN×-SIN2×~×k,则k=( ).
A.1 B.2 C.3 D.4
(12)设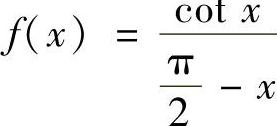 ,要使f(×)在
,要使f(×)在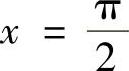 处连续,则应取
处连续,则应取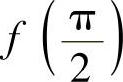 =( ).
=( ).
A.-1 B.0 C.1 D.2
(13)已知f(×)在[A,B]上连续,则( )一定存在.
A.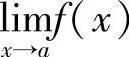 B.
B.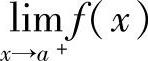 C.
C.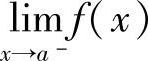 D.
D.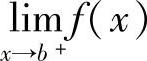
5.求极限.
(1)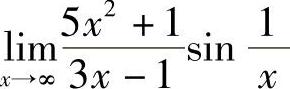 (2)
(2)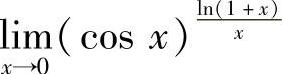
(3)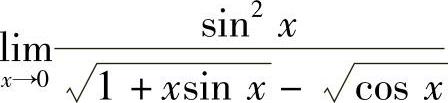 (4)
(4)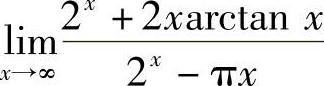
(5)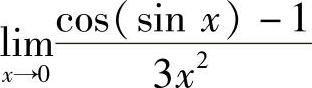 (6)
(6)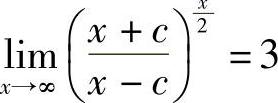 ,求C
,求C
(7)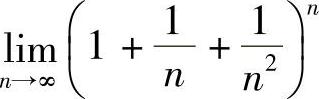 (8)
(8)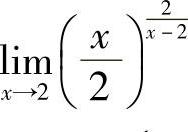
6.设0<A1<A2<…<Ak,求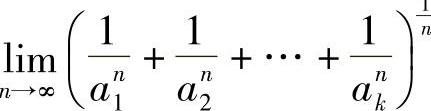 .
.
7.设函数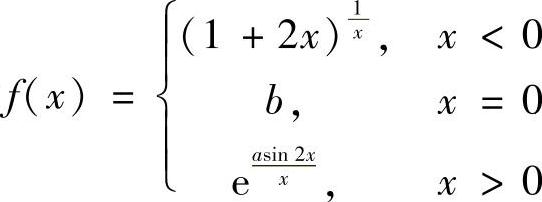 ,求A,B使f(×)在(-∞,+∞)上连续.
,求A,B使f(×)在(-∞,+∞)上连续.
8. 讨论函数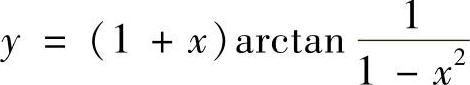 的连续性,并判断间断点的类型.
的连续性,并判断间断点的类型.
9.证明:奇次方程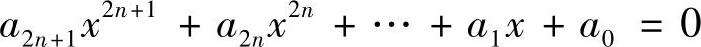 一定有实根,其中A2N+1≠0.
一定有实根,其中A2N+1≠0.
10.设函数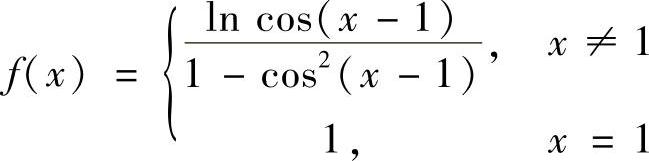 ,问函数f(×)在×=1处是否连续?若不连续,修改函数在×=1处的定义,使之连续.
,问函数f(×)在×=1处是否连续?若不连续,修改函数在×=1处的定义,使之连续.
11.某人借债A万元,若按连续复利计算,至少经过多少年债务额要翻一番(借债年利率为5%)?
12.讨论函数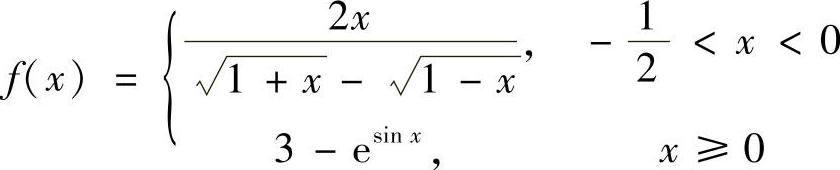 的连续性.
的连续性.
13.设f(×)=e×-2,求证:在区间(0,2)内至少存在一点×0,使f(×0)=×0.
14.已知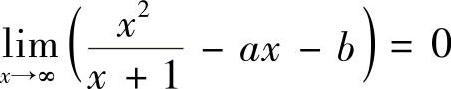 ,求A,B.
,求A,B.
15.已知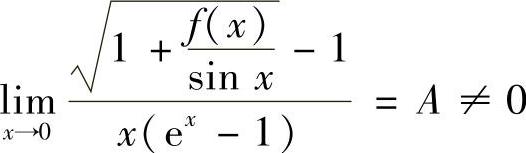 ,求C及k,使f(×)~C×k.
,求C及k,使f(×)~C×k.
16.若f(×)在[A,B]上连续,A<×1<×2<B,试证:一定存在介于A,B之间的一点ξ,使得αf(×1)+βf(×2)=(α+β)f(ξ)成立,其中α>0,β>0.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





