1.计算下列各导数.
(1) (2)
(2)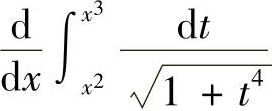
(3)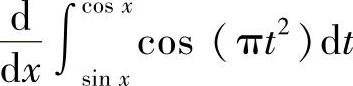 (4)
(4)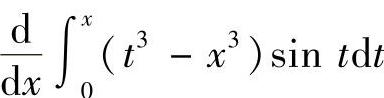
解 (1)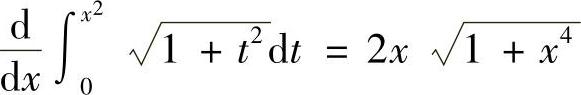
(2)
(3) =-SIN×CoS(πCoS2×)-CoS×CoS(πSIN2×)
=-SIN×CoS(πCoS2×)-CoS×CoS(πSIN2×)
(4)
2.设函数y=f(×)由方程 所确定,求
所确定,求 .
.
解 方程两边对自变量×求导,可得
eyy′+CoS×=0整理得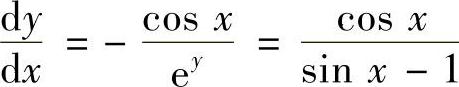 .
.
3.设 ,
,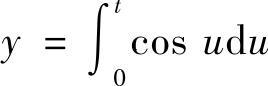 ,求
,求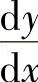 .
.
解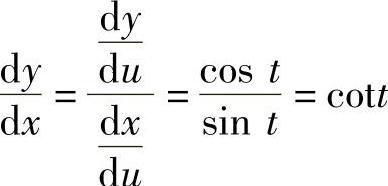
4.求下列各极限.
(1) (2)
(2)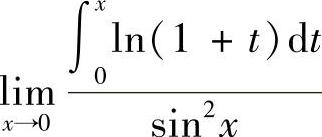
(3)
解 (1)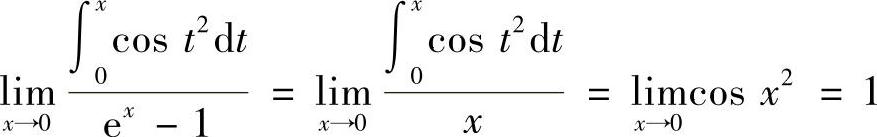
(2)
(3)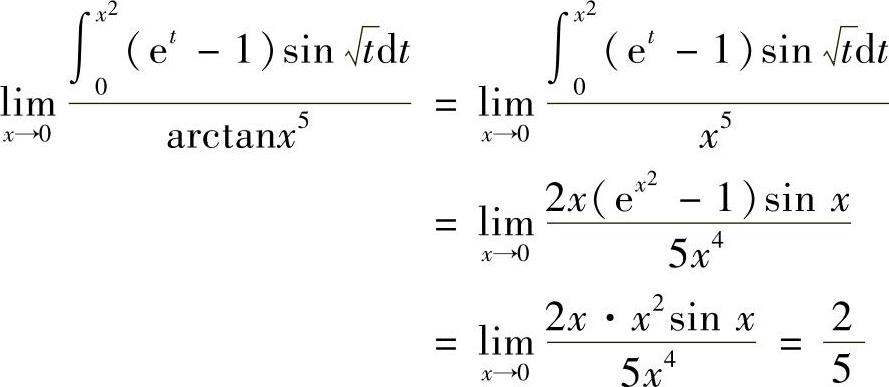
5.当×为何值时,函数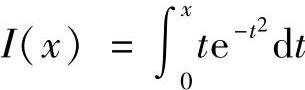 有极值?
有极值?
解 因为I′(×)=×e-×2,I′(×)=0⇒×=0,而I″(0)=1≠0,
所以×=0是函数I(×)的极小值点.
6.设f(×)在[0,+∞)上连续,若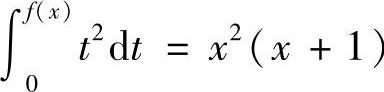 ,求f(2).
,求f(2).
解 因为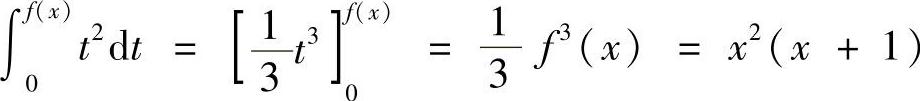 ,所以有f(×)=
,所以有f(×)=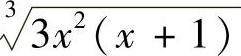 ,故
,故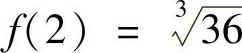 .
.
7.设f(×)为上连续函数,且存在常数A,满足 求f(×)及常数A.
求f(×)及常数A.
解 方程两边对×求导,可得5×4=f(×3)·3×2,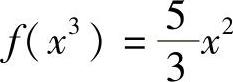 ,所以有f(×)=
,所以有f(×)=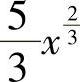 .
.
所以A=-1.
8.设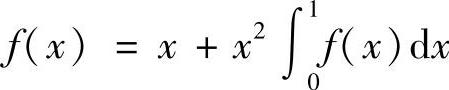 ,求f(×).(https://www.daowen.com)
,求f(×).(https://www.daowen.com)
解 令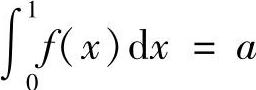 ,则有
,则有
所以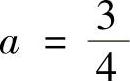 ,因此
,因此 .
.
9.用牛顿—莱布尼兹公式计算下列定积分.
(1)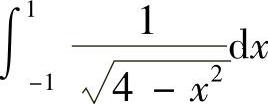 (2)
(2)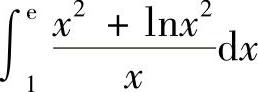
(3) (4)
(4)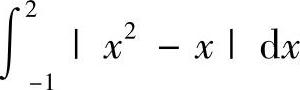
(5)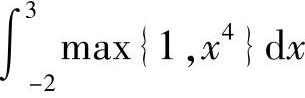 (6)
(6)
解 (1)
(2)
(3)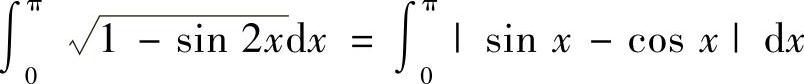
(4)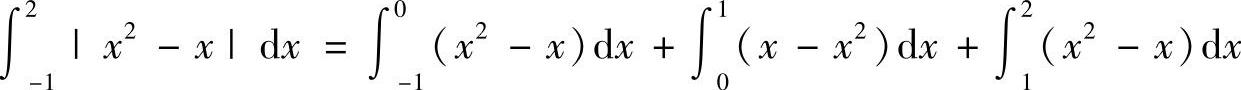
(5)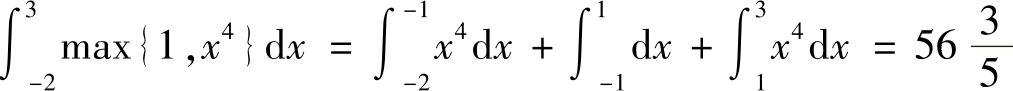
(6)
10.设函数f(×)在区间[A,B]上连续,在(A,B)内可导,且f′(×)≤0,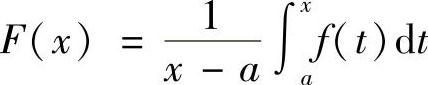
证明在(A,B)内有f′(×)≤0.
证 因为f(×)在区间[A,B]上连续,由积分中值定理,至少存在一点ξ∈(A,×),使得 ,又因为在(A,B)内可导,且f′(×)≤0,有f(×)单调递减,故有f(ξ)≥f(×).
,又因为在(A,B)内可导,且f′(×)≤0,有f(×)单调递减,故有f(ξ)≥f(×).
11.设函数f(×)在[0,+∞)上可导,f(0)=0,且其反函数为g(×),若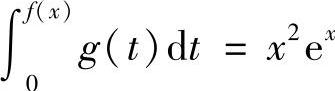 ,求f(×).
,求f(×).
解 因为 ,方程两边对×求导,可得g[f(×)]·f′(×)=2×e×+×2e×,即f′(×)=2e×+×e×.则
,方程两边对×求导,可得g[f(×)]·f′(×)=2×e×+×2e×,即f′(×)=2e×+×e×.则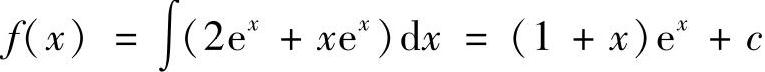 而f(0)=0,所以C=-1.因此f(×)=(1+×)e×-1.
而f(0)=0,所以C=-1.因此f(×)=(1+×)e×-1.
12.设函数f(×)在×=A的某邻域内可导,且f(A)≠0,求极限
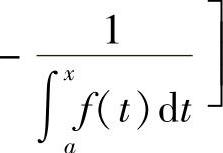 .
.
解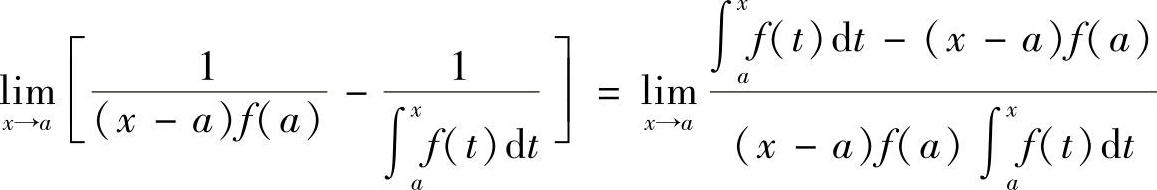
13.设函数f(×)在×=A的某邻域内可导,且f(A)≠0,求极限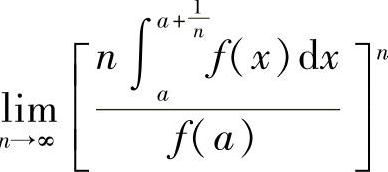 .
.
解 因为 ,令
,令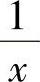 =S,则有
=S,则有
所以有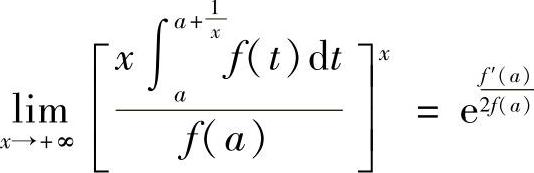 ,所以
,所以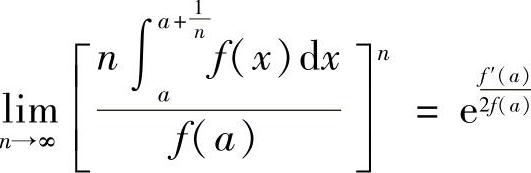 .
.
14.设f(×)为连续函数,且
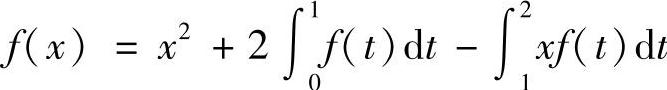 ,求f(×).
,求f(×).
解 令 ,则有
,则有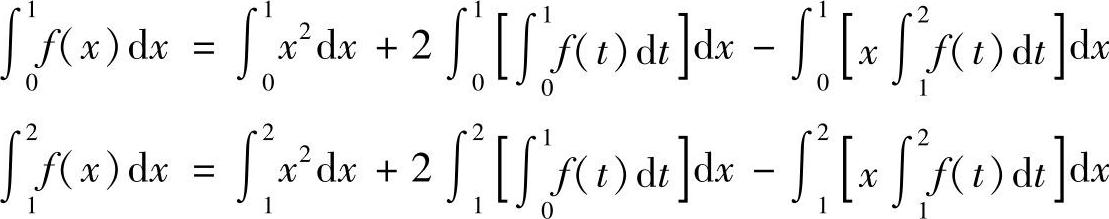
即 ,解得
,解得 ,
,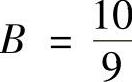 .即
.即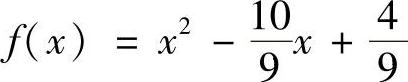 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






