3.5 波浪

3.5 波浪

波浪是海水运动的形式之一，是海水在外力、重力与海水表面张力共同作用的结果。不同外因引起的波浪的周期和波幅均不相同。1965年Kinsman根据波浪周期，结合主要扰动力和恢复力来划分波浪的类型，并给出其能量的近似分布，如图3-4所示。波动周期最短的为毛细波，周期大于5min的长周期波起因于地震、海啸或风暴，而能量分布最显著的为周期处于1～30s，特别是4～16s这一范围内的重力波，在海洋工程中占据重要的地位，是海洋建筑物需要考虑的主要波浪荷载。

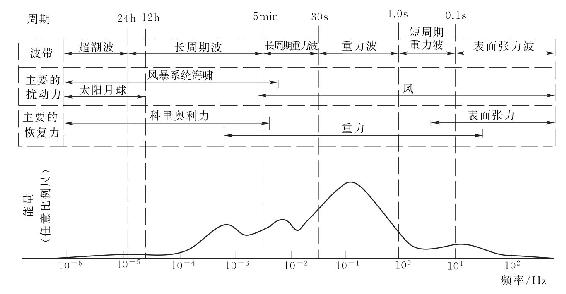
图3-4 波浪周期、能量与类型^[15]

对于由风引起的重力波，它是风浪、涌浪和近岸波浪的总称。风浪主要是指在风直接作用下产生的波浪。涌浪指风停止、转向或离开风区传播至无风水域的波浪。涌浪传播至浅水区，由于受到水深和地形变化的影响，发生变形，出现波浪的折射、绕射和破碎而形成近岸波浪^［3］。

3.5.1 波浪要素

规则波是一种对波浪传播形式的理想化处理，认为波浪具有二维波动的特点，通常假定波浪以一定的周期、波长和波高在水中传播，如图3-5所示。图3-5中波浪剖面高出静水面的部分称为波峰，波峰的最高点称为波峰顶。同样的，波浪剖面低于静水面的部分称为波谷，波谷的最低点称为波谷底。垂直波浪传播方向上波峰顶的连线为波峰线。与波峰线正交的线为波浪的传播方向，波向和风向一样，指波浪的来向，可分为16个方位。相邻波峰顶和波谷底之间的垂直距离为波高，通常以H表示，单位为m。相邻波峰顶（或波谷底）之间水平距离为波长，通常以L表示，单位为m。而波浪周期指的是波浪起伏一次所需的时间，或相邻两波峰顶通过空间固定点所经历的时间间隔，通常以T表示，单位为s。顾名思义，波速指的是波浪的移动或传播速度，通常以C来表示，单位为m/s，大小等于波长与周期之比，即C=L/T。波高与波长之比则为波陡，用δ表示，即δ=H/L，海洋上常见的波陡范围为1/30～1/10。波陡的倒数则为波坦^［3］。

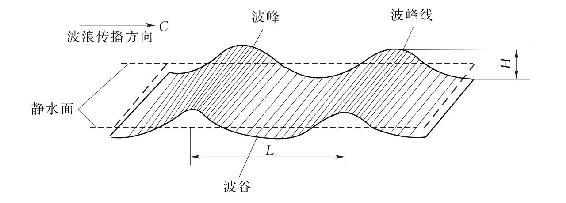
图3-5 规则波的波浪要素^［3］

海洋中波浪的波动实际为不规则波，波面各点的波动形状和大小随不同时间和地点在时刻发生变化，作为随机变量需根据统计特征量来描述。如图3-6所示，横轴表示时间，同时代表静水面，纵轴表示波面相对于静水面的垂直位移。波面自下而上跨过横轴的交点称为上跨零点（如点0、点9）。自上而下跨过横轴的交点称为下跨零点（如点3、点6）。相邻的两个上跨零点（或下跨零点）间的时间间隔称为周期。对于不规则波，各个周期是不等的，通常取其平均值作为平均周期

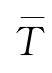
-。在一个周期内波面的最高点为波峰顶（如点4），波面的最低点为波谷底（如点2），波峰顶与波谷底之间的垂直距离为波高，显然图中各个波高也不相等，取其平均值作为平均波高

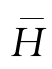
-。统计表明，无论是采用上跨零点还是下跨零点定义波高与周期，其平均值是基本相同的

^［7］

。

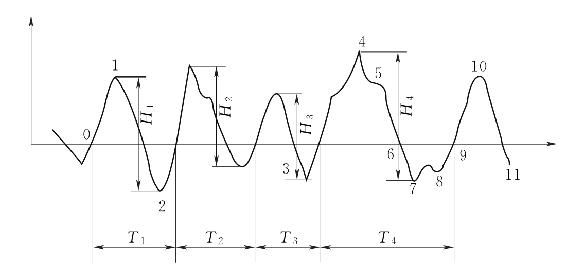
图3-6 不规则波的波浪要素^［7］

在进行波浪要素统计时，多采用上跨零点方法。但在破波带，此处的波剖面明显地向前倾斜，此时波浪具有明显的不对称性，最大波浪力常发生在波前拍击结构物时，故国际水力学研究协会建议采用下跨零点法。

3.5.2 特征波与分布

鉴于波浪的随机特性，在进行波浪研究和分析时通常假定其为平稳随机过程和各态历经随机过程。平稳随机过程确保样本实测记录的时间起点不影响推求结果，各态历经随机过程保证了采用任意一个样本均可代表总体。关于特征波的一些统计分布特性均是基于这两个前提而得出的。

根据不同的统计分类标准，可以采用不同的特征波表示方法。对于特征波的定义，欧美国家多采用部分大波的平均值，苏联多采用超值累积概率法，我国港口与海港工程领域多采用超值累计概率法，我国海上石油工程领域多采用部分大波法。

当采用部分大波法时，平均波采用

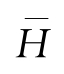
-和

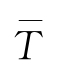
-表示，指波列中所有波浪的平均波高和平均周期。有效波采用

H

_1/3

和

T

_1/3

表示，分别指按照波高大小次序排列后，取前面1/3部分波的平均波高和平均周期。1/10大波采用

H

_1/10

和

T

_1/10

表示，分别指按照波高大小次序排列后，取前面1/10部分波的平均波高和平均周期。最大波采用

H

_max

和

T_H

max表示，指波列中波高最大的波浪和其周期。

当采用超值累积概率法时，H_F指在波列中超过此波高的累积概率为F对应的波高大小，常用的波高类型包括H_1%、H_4%、H_5%和H_13%等。

当波谱为窄带谱时，波面分布服从正态概率分布，波高分布服从瑞利分布，进而可以理论上分析得出不同波高分布与平均波高的关系。

对于深水波，累计概率特征波高

H

_F

与平均波高

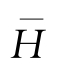
-的关系为

^［16］

不同累计概率下特征波高

H

_F

与平均波高

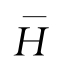
-的具体比值如表3-7所示。

在浅水区域，考虑浅水效应后累计概率特征波高

H

_F

与平均波高

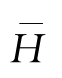
-的关系为

^［16］

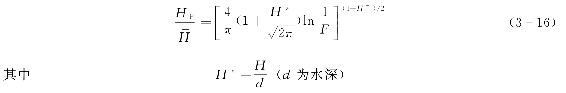
对于1/

p

部分大波特征波高

H

_1/p

，深水条件下其与平均波高

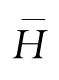
-的关系为

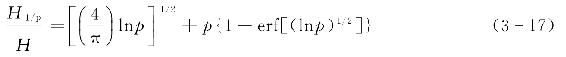
式中 erf——误差函数。

部分大波波高

H

_1/p

与平均波高

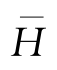
-的具体比值如表3-8所示。

在浅水区域，考虑浅水效应后部分大波波高

H

_1/p

与平均波高

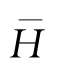
-的关系为

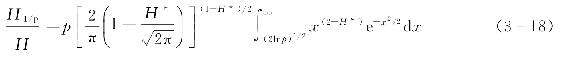
无论是基于深水波波高的瑞利分布还是浅水下波高的格鲁霍夫斯基分布，波高值的上限都是无限的，而在工程实际中最大波高均为有限值。当最大波高作为一个随机变量，其与波高样本个数

N

₀

和波高分布形式有关。结合波高平均值与有效波波高的关系

H

_1/3

=1.598

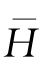
-，最大波高的众值、均值和累积率

μ

%对应的最大波高与有效波高关系

^［17］

如下：

众值最大波高（H_max）_m为

均值最大波高

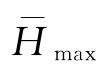
为

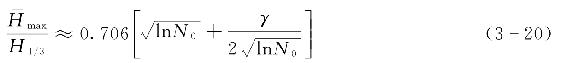
式中 γ——欧拉常数，γ≈0.5772。

累积率为μ%的最大波高（H_max）_μ%为

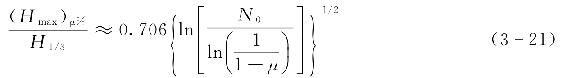
对于浅水条件下，最大波高与平均波高的关系更为复杂，可以参考相关文献。

波浪的波长服从瑞利分布，则根据线性波中波浪波长与周期的关系，可得到周期T的分布。其分布函数为^［17］

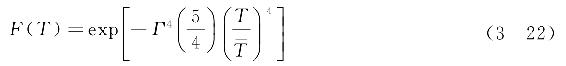
式中

Γ

——伽马函数，其中

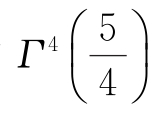
=0.675；

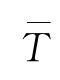
——平均周期。

统计数据表明，波浪周期的概率密度函数的离差系数C_V≈0.283，偏态系数C_s≈0；而波高的离差系数C_V≈0.552，偏态系数C_s≈0.635。可见周期的分布比波高的分布更集中（周期的离差系数C_V更小），且几乎是对称的（周期的偏态系数接近0），因此波浪周期中出现机会最多的是平均周期。

海浪由深水进入浅水后，平均周期几乎不变。浅水周期的分布规律与水深无关，且变化很小。不同累积频率波高对应的周期是不同的，但它们只是统计出来的大致规律，理论关系还未完全确定。为简化起见，一般均将设计周期采用平均周期

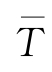
。对于大的波高，其波周期的分布比较集中于平均周期附近；对于较小的波高，其波周期的分布就比较分散。亦即，对于大的波高，一般不会遇到比平均周期大得很多的波周期；而对于小的波高，则有可能遇到比平均周期大得多的波周期

^[3]

。

若当地大的波浪主要为风浪，可由当地风浪的波高与周期的相关关系外推与该设计波高相对应的周期，或按表3-9确定相应的周期。

当地大的波浪主要为涌浪或者混合浪时，可采用与波浪年最大值相对应的周期系列进行频率分析，确定与设计波高为同一重现期的周期值。

日本的合田良实根据现场实测资料，统计得出波浪周期的相互关系为

在工程上，也可以近似按照如下关系式来确定波浪周期^［16］，即

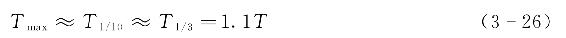
一般最大波高H_max和最大波周期T_max并不一定对应同一个波，其他特征值下的波高与周期也不一定对应同一个波，但在工程上二者往往配对使用。

3.5.3 我国近海波浪

我国近海波浪的形成、发展和消衰主要取决于风的盛衰，此外地形和岛屿对局部地区的海浪也会产生不同程度的影响。

就波浪方向而言，我国海区冬季盛行偏北浪，夏季盛行偏南浪，春秋为过渡季节。渤海于9月首先出现偏北浪，随后由北向南逐渐发展，至10月则可遍及东海、南海北部和中部。夏季盛行偏南风，因而以偏南浪为主。与冬季相反，它首先在南海出现，再逐次向北发展。早在5月，在南海南部即出现南向浪，至6月西南风盛行后，整个南海遍布西南向海浪，到7月，最北的渤海也盛行偏南浪。

就波浪平均周期而言，国内海区中波浪平均周期冬季最大，12月至翌年2月，大部海区的风浪周期在4～5s，在夏季降至3s左右。在大浪中心海域，周期增大，如南黄海年平均为6s，东海、台湾周围至南海中部可达6～7s。涌浪周期与涌高有对应关系，在大涌区，冬季各月和夏季7—8月的周期较大，过渡季节的周期小。就海区而言，一般北部小而南部大。例如渤海的周期，几乎全年均小于4s；而黄海到东海逐渐增大，至东海南部可达7～8s。在南海，则以北部湾海区较大，其他海区一般年平均为5s左右。

就波浪波高而言，冬季因各海区平均风力最大，平均波高亦最大，自10月开始，各海区平均波高渐增至1.5m以上，台湾海峡至南海中部可达2.0m以上，且大多能保持到翌年2月。夏季整个海区平均波高一般都显著降低，进入6月，渤海、黄海北部、朝鲜半岛西岸的浪高不到1m，其他海区也在1.2m以下。7—8月，由于台风活动，南部海区的浪高有所增加，强台风过境时浪高可达8～10m。

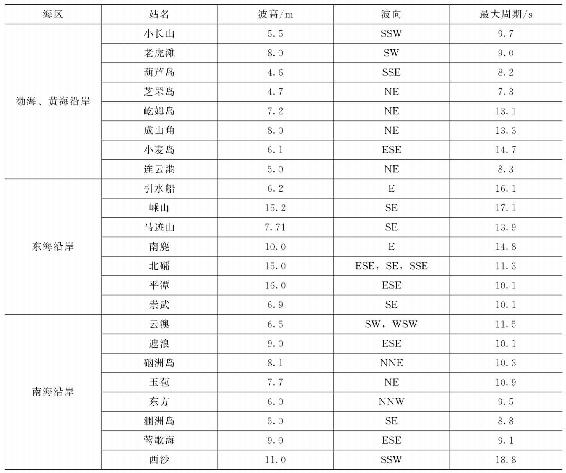
我国沿海大浪受台风和寒潮大风影响十分明显。冬季在寒潮大风作用下，北方沿海波高较大；夏季东南沿海受台风影响，南方沿海波高较大。波高超过10m与周期10s以上的大浪多出现在开敞的东海。中国沿海最大波高分布如表3-10所示。