4.4 孤立波（Solitary波）

4.4 孤立波（Solitary波）

波浪理论中，波浪运动是周期的或近似周期的运动。线性波为周期波，波浪质点沿着封闭椭圆轨迹线作振荡运动，没有净位移。斯托克斯波在传播方向上有质量迁移，水质点的运动轨迹不再是一个封闭的椭圆或圆形，而是呈螺旋状向前前进的连续曲线，进而存在一个净位移。与上述波浪理论不同，还存在一种特殊的情形，波浪质点仅在波浪传播方向运动，称为移动波，孤立波属于这种类型。

4.4.1 运动形态

纯粹的孤立波全部波剖面在静水面以上，波长无限，如图4-8所示。设波峰沿正x方向传播，当波峰位于水面质点1的左侧很远距离时，质点1的运动可以忽略。随着波峰的移进，质点1开始向上并向右运动。波峰经过时，质点1上升至最高位置。当波峰移去后，此质点倾斜下降，直至波峰传至相当远为止，质点又恢复几乎无运动的状态。质点1的运动轨迹为一抛物线，由于波峰经过而移动了一段水平距离。质点2的运动轨迹与质点1相似，水平移动距离也大致相同，但其上升的高度比质点1要小。遵循同样的规律，质点3沿底面移动类似的距离。

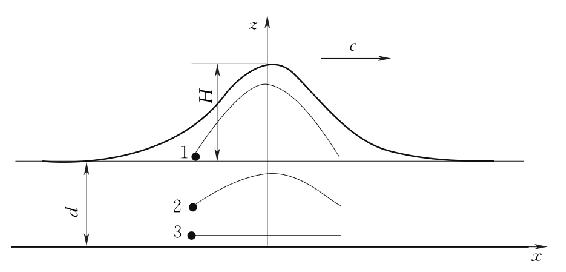
图4-8 孤立波波剖面、坐标系和相关变量^［4］

在自然界中纯粹的孤立波是难以形成的，但当波浪传至近岸浅水区接近破碎时的波面形状和运动特性与孤立波比较接近。因此海洋工程中为研究波浪的破碎水深、泥沙运动以及分析破碎波对海工结构物的作用等问题中，孤立波理论得到了广泛应用^［1］。

4.4.2 特征参量的求解

孤立波理论的求解可以按照两个途径来进行：一是根据无旋运动的假定，求出满足自由面以及海底条件的解答^［5］；二是作为椭圆余弦波的一种极限情况，从椭圆余弦波理论来求解。由于第二种方式应用较多，且求解较为方便，以下给出这一方式的计算过程。

当模数k=1时，根据式（4-61）和式（4-64）可得，K（k）→∞，E（k）=1。此时还存在关系式cn（u，1）=sech（u）。根据式（4-60），且k=1，进而得到

根据式（4-81），且K（k）→∞，因此孤立波的波长L→∞。

将式（4-81）和E（k）=1以及L→∞代入式（4-66），可得波谷距离海底的距离z_t为

进一步，将关系式cn（u，1）=sech（u）和式（4-81）代入式（4-70），可得静水面以上的波面高度η为

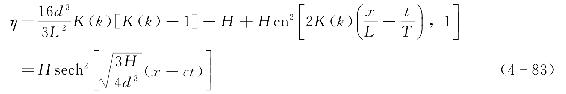
式中 x——起点设在波峰处；

c——孤立波的波速。

将模数k=1和K（k）→∞代入式（4-62）可得孤立波的波速c为

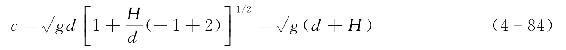
类似的，将模数k=1代入式（4-71）和式（4-72）可得到孤立波的速度分布。近似取一阶而略去高阶项，波浪质点的水平向和竖向速度u_x、u_z分别为

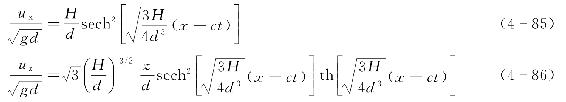
通过以上各表达式可以看出，决定孤立波波动性质的主要因素是H/d。当H/d增大至一定程度时，波峰附近的波面将产生破碎现象。不同的学者曾给出不同的H/d极值，一般介于0.714～1.03之间，常用值为0.78。McCowan（1891）假定波峰水质点速度等于波速时产生破碎，得到水深与波高的关系式为^［6］