4.1 线性波(Airy波)
4.1 线性波(Airy波)
微幅线性波理论是应用势函数来研究波浪运动的一种线性波浪理论。线性波是一种简化了的最简单的波动,其水面呈现简谐形式的起伏,水质点以固定的圆频率ω作简谐振动,如图4-1所示。同时波形以一定的速度c向前运动,波浪中线(平分波高的中线)与静水面重合。线性波理论最初由Airy提出,故又称为艾瑞波(Airy波)。该理论求解中假定波面高度η与波长L之比为一小量,故也称作微幅波。微幅线性波的波剖面与坐标系如图4-1所示。
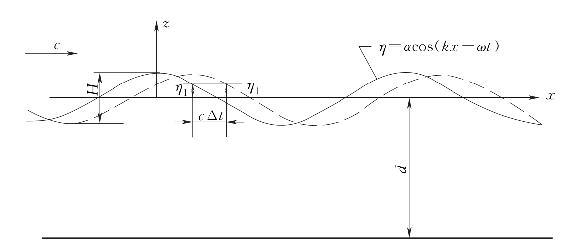
图4-1 微幅线性波的波剖面与坐标系
4.1.1 基本原理与方程
线性波是一种最简单的波浪求解理论,该理论基于众多假定条件而提出,这些假定条件包括[1]:
(1)流体是无黏性不可压缩的均匀流体。
(2)流体作有势的运动。
(3)重力是唯一的外力。
(4)流体表面上的压强等于大气压。
(5)海底为水平的固体边界。
(6)波幅或者波高相对于波长是无限小的,流体质点的运动速度是缓慢的。
按上述6条假定的最后一条,可以认为波动的自由表面所引起的非线性影响可以忽略,即非线性的自由表面运动边界条件和动力边界条件可以简化为线性的自由表面边界条件。
在重力场中处于平衡的液体的自由面为一平面。如果在某处外来干扰的作用下,液体自由表面的各个质点将离开其平衡位置,但失去平衡状态的各液体质点在重力和惯性力的作用下,有恢复初始平衡位置的趋势,于是形成了液体质点的振荡运动,并以波的形式沿整个表面传播。对于势波,只要得到波动海域的速度势φ便可求得各点的速度,因此研究势波的问题归结为寻求波动海域的速度势φ。
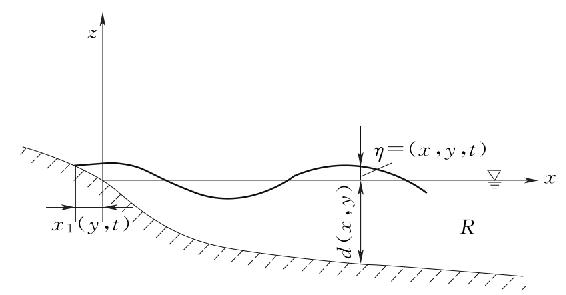
图4-2 波动海域R示意图[1]
对于如图4-2所示的海域R,其速度势应满足拉普拉斯方程,即
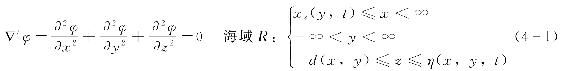
式中 x、y、z——笛卡尔坐标变量;
x s(y,t)——t时刻海域和陆域交线上的x坐标;
η(x,y,t)——自由水面的铅直位移;
d(x,y)——水深变量函数。
由于式(4-1)边界约束条件中函数xs(y,t)和函数η(x,y,t)均为未知函数,因此拉普拉斯方程的求解域不仅随时间而变,而且本身也是要求解的一部分。对于线性波,为了能唯一确定速度势φ,所需要的边界条件包括海域底部运动边界条件、自由表面运动边界条件和自由表面动力边界条件。
采用势函数表示的海域底部运动边界条件为(变量d为水深)

采用势函数和波面函数表示的自由表面运动边界条件为

采用势函数和波面函数表示的自由表面动力边界条件为(g为重力加速度)

式(4-3)和式(4-4)所描述的边界条件可以合并为

综上可知,常深度下二维线性波的速度势φ(x,z,t)由以下基本方程和边界条件所确定,即
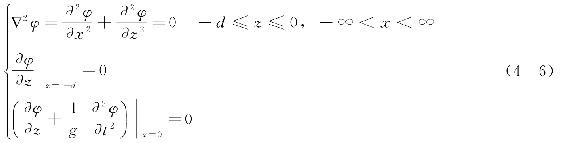
因为研究的是随时间作简谐振动的周期解答,显然可以不考虑初始条件,可以从设定一个反应时间周期性变化的速度势来进行分析。
4.1.2 特征参量的求解
波浪理论中经常用的变量包括波速c和波数k,它们与波浪的波长L、周期T和频率f、圆频率ω的关系为
波速为

波数为

圆频率为

波浪推进中不同波长(频率)的水波以不同的速度传播,从而导致波浪分散现象的产生,在波浪理论中称为色散关系或频散关系,关系式为

基于式(4-7)~式(4-10),可以推得有限水深条件下(0.05<d/L<0.5)波浪的周期、波长和波速三者之间相互关系为
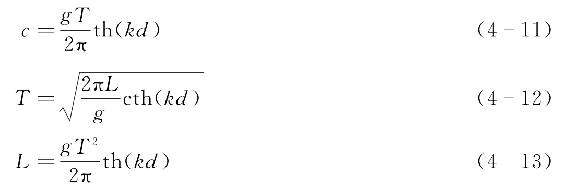
在深水条件下(d/L≥0.5),波浪的周期、波长和波速三者之间的关系为

在浅水条件下(d/L≤0.05),波浪的周期、波长和波速三者之间的关系为

当水深为有限时,常深度二维线性波的速度势表达式为
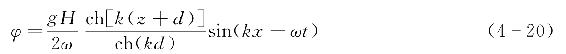
式中 H——波高。
波面位置η对应的波面方程为

不同相位和深度位置下波浪质点的水平速度ux和垂直速度uz分别如式(4-22)和式(4-23)所示。
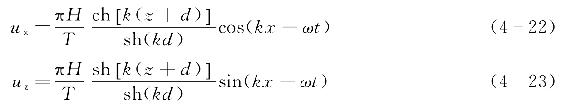
不同相位和深度位置下波浪质点的水平加速度ax和垂直加速度az分别如式(4-24)和式(4-25)所示。
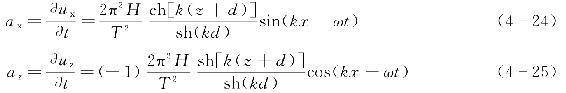
4.1.3 波浪质点运动轨迹
对于线性波,波动场内波浪质点的运动轨迹为一椭圆,即质点沿着封闭椭圆轨迹线作振荡运动。其运动轨迹方程为
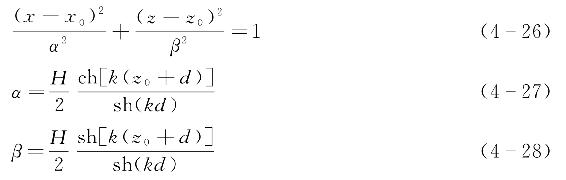
式中 x0、z0——波浪质点静止时水平与竖向位置坐标;
H——波高;
k——波数。
进一步可以发现,式(4-26)~式(4-28)描述的椭圆长半轴α和垂直向短半轴β决定于波浪质点静止位置的纵坐标z0,而与水平坐标x0无关。
对于深水条件,由式(4-26)~式(4-28)可得波浪质点的运动轨迹方程为
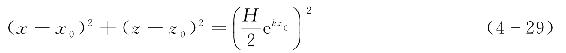
由式(4-29)可见,深水条件下波浪质点的轨迹是一个半径r为(H/2)ekz0的圆,即水质点沿着闭合圆轨迹作振荡运动。在水面处z0=0,质点运动轨迹线圆的半径r0=H/2。随着深度的增加,质点运动轨迹圆的半径r迅速减小。
水深对波浪运动起着很大的影响。在深水(d≥0.5L)中的波浪为深水波;在浅水(0.05L≤d<0.5L)中的波浪为浅水波;在极浅水(d<0.05L)中的波浪为极浅水波。这3种波浪其水质点的运动轨迹、水平速度和垂直速度随深度的变化如图4-3所示,图4-3中位于左侧的图形为质点运动轨迹,右侧图形为质点水平速度和垂直速度沿水深变化曲线。
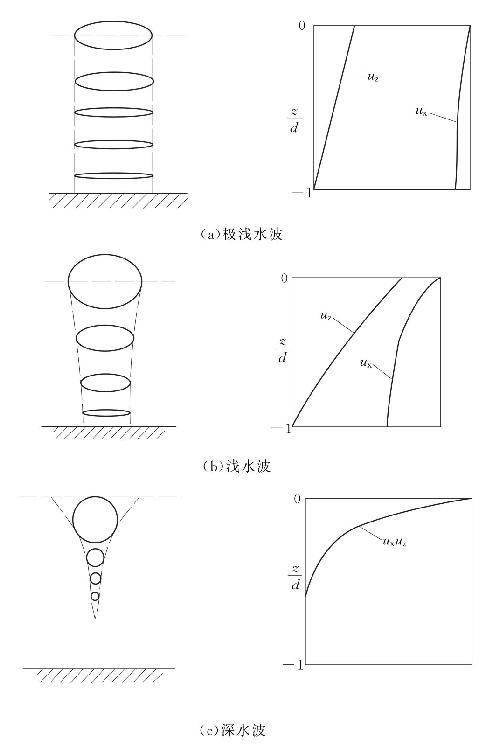
图4-3 质点轨迹、水平速度和垂直速度随深度变化示意图[1]
