4.6 波浪理论的适用范围

4.6 波浪理论的适用范围

波浪理论是通过某些假设与简化而得到的，由于不同的简化与假设，理论计算结果有别，也各有其适用范围。为确定各种波浪理论的适用范围，不少研究者进行了大量理论分析和实验检测。这些研究大多是针对波面形状、波速、水质点运动速度和加速度、水质点运动轨迹形状、波浪的极限波陡等波浪特性确定的。

在讨论波浪理论中常遇到水深的划分问题，即如何确定浅水、深水的标准。根据国内外相关研究成果，水深通常划分为3个范围，即浅水、过渡水深和深水。通常而言，单独划分水深的范围并无实际意义，应和具体的波浪性状相结合来进行判断。不同水深判定的标准如下：

（1）深水：d/L=0.500 或d/gT²=0.0792。

（2）浅水：d/L=0.04或d/gT²=0.00155。

（3）过渡水深：位于深水和浅水之间的区域。

在深水条件下影响波浪波动性质的主要因素是波陡（H/L），在浅水条件下影响波浪波动性质的主要因素是波陡（H/L）和相对水深（d/L），而在极浅水影响波浪波动性质的因素是相对波高（H/d）。迄今为止尚无一种波浪理论可以普遍地适用任意水深的波况，各种波浪理论只能适用于各自特定的波况条件。挪威船级社DNV—OS—J101标准^［10］给出了波浪理论适用的定性描述，线性波仅适用于深水区的小振幅波，斯托克斯波适用于有限振幅的波况，流函数则适用于更广范围下的波浪分析，布辛奈斯克高阶波则适用于浅水波，而椭圆余弦波则适用于极浅水条件下的波浪分析。

在应用波浪理论进行海上测风塔基础结构受力分析之前，需要根据特定的海洋环境条件来确定合适的波浪理论。纵观国际上对波浪理论适用范围的研究成果，Dean（1970）、Le Méhauté（1976）和Komar（1978）等先后对此进行了详细分析，并将试验测量数据与理论计算结果进行了比较^［11-12］。

挪威船级社DNV—OS—J101标准中，采用波陡系数（S）、相对水深（μ）和Ursell数（U_r）等3个参量来作为波浪理论选择的标准，这3个系数的定义表达为

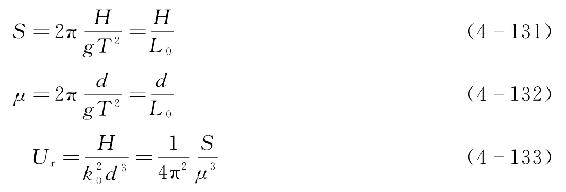
式中 H——波高；

T——波浪周期；

L ₀——深水波长；

d——水深。

结合上述的3个参量，波浪理论适用的范围如表4-5所示。图4-12为波浪实测试验数据与表4-5这一适用范围规定的验证关系。

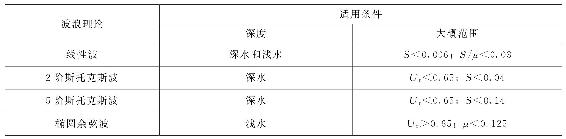
基于Le Méhauté的分析结果，美国《海滨防护手册》中给出了如图4-13所示的波浪理论选择方法。

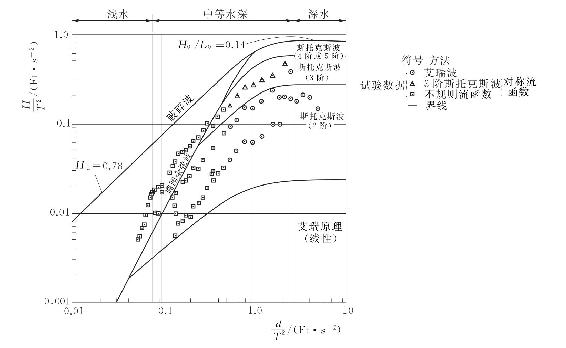
图4-12 试验结果与波浪理论选择对比

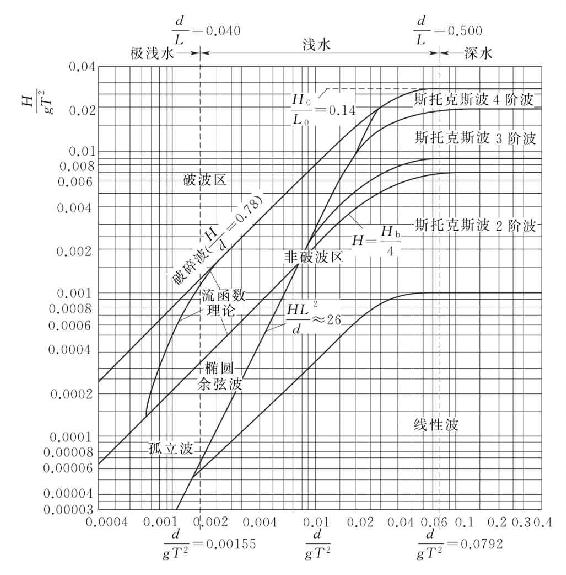
图4-13 不同波浪理论适用范围^［13］

图4-13中采用无量纲参量H/gT²和d/gT²分别为纵、横坐标。两条实线为波浪破碎限界，其中深水波的破波限界是（H₀/L₀）_b=（H₀/L₀）_max=0.142［参见式（4-59）］，浅水波的破波限界是（H/d）_b=（H/d）_max=0.78［参见式（4-87）］。图4-13中与纵坐标平行的两条虚线分别是深水波限界d/L=0.5和浅水波限界d/L=0.04，也即本节开始部分的水深类别判定标准。

上述破碎波破波界限未考虑海底坡度的影响。当考虑海底岸坡坡度对波浪破碎的影响效应后，对于无流规则波条件下的波浪破碎指标确定为^［14］

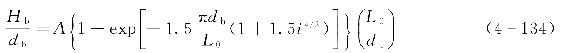
式中 L₀——深水波长；

H _b——破碎波波高；

d _b——水深；

i——海底坡度；

A——常数，由破碎波波峰时水面水质点水平速度达到波速的临界值可得A≈0.17。

当海底坡度i不小于1/50并有水流存在时，波浪受流的影响将变形。如果取波浪相对于水流的波周期T_r（T_r≠T，T为绝对波周期），并以T_r计算深水波长，则式（4-134）仍然成立，且A=0.17^［15］。

Nelson（1983，1987）指出，当岸坡平缓（i≤0.01）时，破碎指标将下降，其可能的最大值为^［16-17］

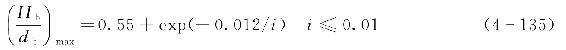
采用式（4-135）确定的不同海底坡度对应的破碎波波高与水深比如表4-6所示。

我国JTS 145—2—2013中也规定了海底坡度i＜1/140时破碎波波高与破碎水深的最大比值，如表4-7所示。当坡度1/140<i<1/50时，比值H_b/d_b的最大值可取0.78。

图4-13中椭圆余弦波与斯托克斯波之间的限界采用Ursell参数L²H/d³=26来划定［注意与式（4-133）中Ursell参数的区别］，其右侧为斯托克斯波和小振幅线性波理论的适用范围，左侧是椭圆余弦波和孤立波理论的适用范围。

Ursell参数分割的右侧区域可近似地再划分成若干区：第Ⅰ区为线性波，其限界为H₀/L₀≈0.00625（H/gT²≈0.001）；第Ⅱ区至第Ⅳ区为斯托克斯2阶至斯托克斯4阶波，其中第Ⅱ区与第Ⅲ区的界限为H₀/L₀≈0.0503（H/gT²≈0.0086）；第Ⅲ区与第Ⅳ区的界限为H₀/L₀≈0.107（H/gT²≈0.0196）。

Ursell参数分割的左侧区域中，椭圆余弦波与孤立波限界为d/L=0.04或d/gT²=0.00155，该界限右侧是椭圆余弦波理论适用范围，左侧为孤立波理论的适用范围^［18］。

上面给出了各波浪理论或方法的适用范围，鉴于流函数这一数值分析方法的广泛适用性，包括挪威船级社DNV规范、德国劳氏船级社GL标准^［19］和美国石油协会的API标准^［20］均给出了流函数分析中函数阶数的选择和适用范围，如图4-14所示。

由图4-14可见，对于斯托克斯波和线性波的适用范围中，采用3阶流函数均能满足分析精度的要求，当位于斯托克斯波和线性波适用范围的左侧（波高更高或水深更浅）时，应加大流函数计算的阶数，通常采用阶数N=11可满足大部分情况下的波浪分析要求。对于极浅水的情况下应采用更高阶的流函数来进行计算分析。

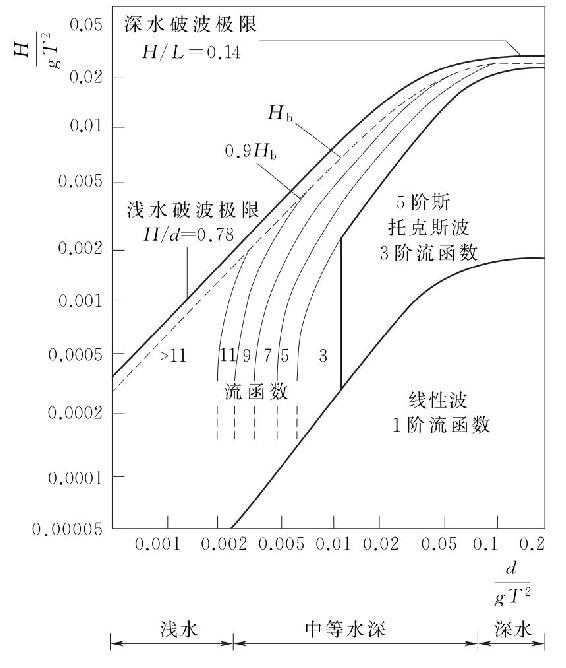
图4-14 流函数方法中阶数N的选择与适用范围