4.2 斯托克斯波(Stokes波)
4.2 斯托克斯波(Stokes波)
线性波采用了对非线性波面边界条件进行线性化处理的假设,对于海洋中波高较小或振幅较小的波浪运动采用线性波来分析是适宜的。但海洋中实际波浪的波面振幅较大时,采用线性波理论这种线性化的处理方法将带来较大的误差[2],为此需要考虑非线性自由表面边界条件的影响。一般而言,严格满足非线性自由表面条件的解答通常难以得出,实际在求解中往往对非线性自由表面条件采用不同形式的拟合方法[3]。非线性波浪理论可分为斯托克斯(Stokes)波、椭圆余弦(Cnoidal)波和孤立(Solitary)波和流函数理论等。本节介绍斯托克斯波,其他几种波浪理论后续依次进行介绍。
与线性波相比,斯托克斯波理论中波高相对于波长不再视为无穷小,考虑了波陡H/L的影响,认为H/L是决定波动性质的主要因素。波面也不再是余弦形式,而是波峰较窄,波谷较宽接近于摆线的形状,如图4-4所示。水质点也不是简单地沿封闭轨迹线运动,而是在波浪传播方向上存在微小的纯位移,即波浪运动中伴随着质量的迁移[1]。
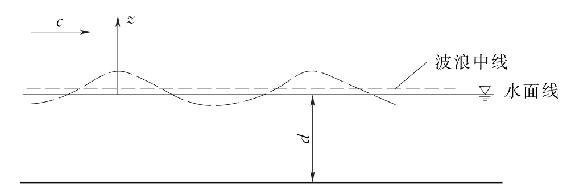
图4-4 斯托克斯波的波剖面与坐标系
4.2.1 分析原理
斯托克斯波求解时,假定波浪运动基本方程解答可以用小参数ε的幂级数展开式来表示。小参数ε是与波动特征值有关的无因次常数,最有效的波动特征值在水深较大时为H/L,而在水深较小时为H/d。设未知的波浪速度势φ和波面高度η为幂级数,即
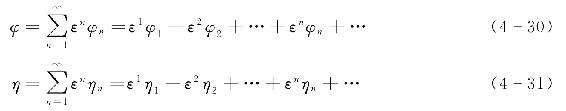
式(4-30)中每一项
φn都是拉普拉斯方程
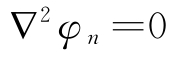
的独立解答,并满足海底边界条件
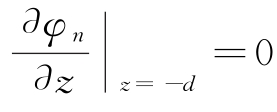
和自由表面的边界条件。
由于自由表面总是在静水面附近,自由表面z=η处的速度势φ可用麦克劳林级数来表示,即可得自由表面的运动学边界条件为
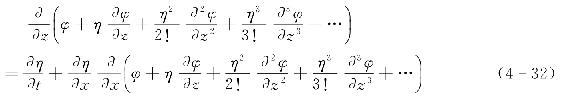
结合二维波动的非线性自由表面动力边界条件的一般表达式,对于斯托克斯波,其自由表面的动力边界条件为
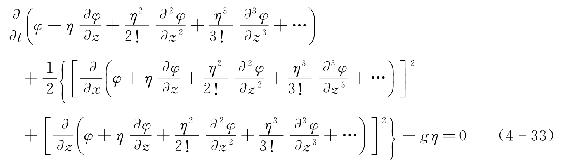
将式(4-30)和式(4-31)代入式(4-32)和式(4-33)后,按小参数ε的幂次归并整理,可得
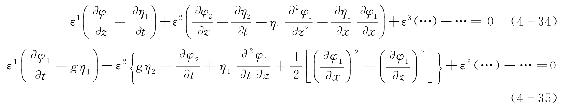
由于小参数ε为小于1的常数,要使上述两式成立,只有使εn前面的各系数为零,这样就得到一系列独立于ε的偏微分方程组。
对应于小参数ε的一阶条件,存在方程组为

对于小参数ε的二阶条件,存在方程组为
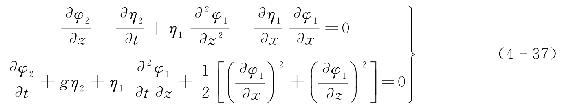 (https://www.daowen.com)
(https://www.daowen.com)
对于小参数ε的n阶条件,任意阶方程组可表示为
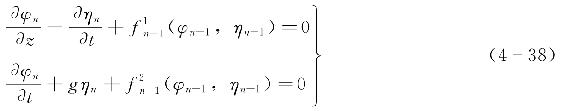
在求得一阶时的φ1和η1后,将结果代入二阶方程组式(4-37),便可以得到同时满足拉普拉斯方程和海底边界条件的φ2和η2。以此类推,可由低阶到高阶逐步解出这些微分方程,便得到各阶的近似解φn和ηn。
关于斯托克斯波,很多学者作了详尽的研究。Miche(1945)导出了斯托克斯2阶波,Skjelbreia(1959)导出了3阶波和5阶波的近似方程[2]。随着阶数的增加,斯托克斯波应用范围也更为广泛,即2阶波、3阶波可以求解的问题,5阶波同样可以求解且所得结果更为精确,以下对海洋工程中广泛采用的斯托克斯5阶波进行分析,相对于斯托克斯2阶波和3阶波的推导过程而言,斯托克斯5阶波的推导过程更为复杂。
4.2.2 斯托克斯5阶波求解
斯托克斯5阶波的计算公式如表4-1所示[1]。
表4-1 斯托克斯5阶波计算公式汇总表

注:表中θ=k(x-ct)=kx-ωt,k为波数。
表4-1中系数Φ′n表达式如表4-2所示。
表4-2 系数Φ′n表达式

表4-1中系数η′n表达式如表4-3所示。
表4-3 系数η′n表达式

表4-1~表4-3中系数Aij、Bij、Ci为与相对水深(d/L)有关的变量,具体表达式为

式中 c1——中间变量,c1=ch(kd);
s——中间变量,s=sh(kd)。
波高H与波面高度η之间存在关系式为

将表4-1中波面高度kη的表达式(波面高度η对应项)和表4-3中系数η′n的表达式一并代入式(4-56)可得
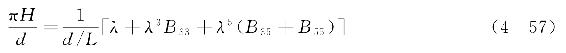
同时表4-1中波速c的表达式可进一步表示为
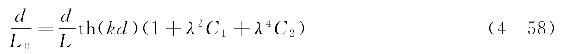
式中 L0——深水波长,L0=gT2/2π。
在已知波高H、波周期T和水深d后,由于系数B33、B35、B55、C1和C2仅是d/L的函数,故可联立求解式(4-57)和式(4-58)组成的超越方程组,一般应通过迭代来求解,进而确定出系数λ和波长L。计算得到系数λ和波长L后,斯托克斯5阶波其他的波浪参数可根据表4-1、表4-2和表4-3中所列关系式来确定。
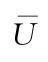 —质点速度;T—周期
—质点速度;T—周期
4.2.3 运动轨迹与极限波陡
与线性波理论不同,采用斯托克斯波理论下波动水质点的运动轨迹不再是一个封闭的椭圆或圆形,而是呈螺旋状向前不断前进的连续曲线,如图4-5所示。进而在波传播的水平方向上产生沿着波动方向的净位移,这种净位移造成了一种水平波动,称为波流。这表明沿着波向不仅有动量和能量的传播,而且也在传输质量,这对泥沙等物质在海洋中的输运具有重要意义。在一个波周期内波浪质点的平均迁移速度沿水深分布是不均匀的,在自由水面处最大,随着深度增加而呈指数规律减小。
波浪观测资料表明,波高和波长的比值(波陡)增大至某一量值时,波峰附近的波面破碎,出现浪花。一般假定当波陡趋于极限时,波峰附近的波面可视为直线,并取波峰顶附近水质点的最大水平速度和波形传播速度相等的状态来作为波陡的极限状态。这是因为当波浪质点的最大水平速度大于等于波速时,质点将脱离波面,故波浪会失稳破碎。采用斯托克斯波按此极限条件给出的极限波陡为
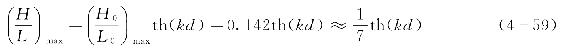
此时对应的波峰顶角为120°,如图4-6所示。而实际观测到的深水极限波陡(H0/L0)max≈1/10。
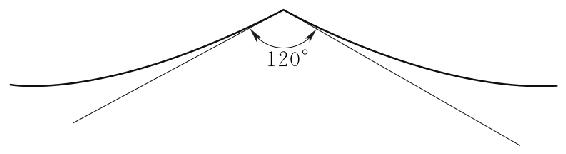
图4-6 极限波峰顶角
