4.5 流函数方法(Stream Function)
4.5 流函数方法(Stream Function)
非线性波理论的解析方法尽管在海洋工程中有所应用,但包含着许多限制条件,例如对于浅水条件下应用斯托克斯波或深水条件下应用椭圆余弦波等理论将使得计算很难收敛,因此20世纪60年代以来不少研究者发展了另一种完全不同的方法——直接数值计算方法来研究波浪的非线性影响。其中应用最为广泛的是1965年由R.G.Dean首先提出的基于流函数采用数值方法来求解非线性边值问题的流函数理论[7]。
4.5.1 分析原理
与斯托克斯波求解中基于傅里叶级数的小参数摄动展开来计算不同,流函数采用直接求解非线性方程来数值确定相关系数。对于不同的求解阶数,采用这种数值处理方法而言更易于扩充实现。整体而言,流函数波理论包括两类[3]:其一是对称的或规则的流函数波理论,描述了对称的周期波,具有预定的周期、波高和水深的不变形波;其二是不规则流函数波理论,流函数和相应波浪运动学参数具有预定的波形,这种理论特别适于分析波浪水池或场试数据。
不规则流函数波理论的一般形式,对波浪形状没有限制。当各种相速度及分量相互作用引起波浪传播和相对运动时,波浪可以改变形状。在规则流函数波理论中,假定波浪以常速c传播,形状不变。若选择与波浪相同方向、相同速度c移动的坐标系,坐标系跟随波浪运动,坐标原点总处于波峰上,在此坐标系中,波形不变,边值问题得以简化。此时,运动是定常的,时间变量消失。相对移动坐标系的水平速度为u—c,微分方程用拉普拉斯方程描述,坐标系如图4-9所示。
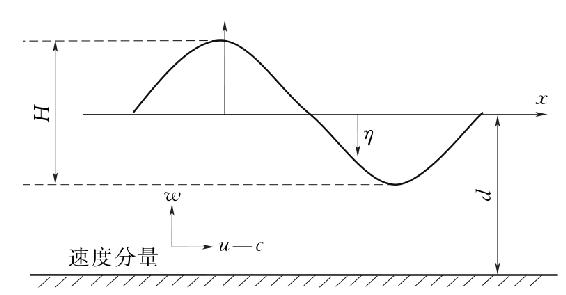
图4-9 分析坐标系定义
求解流体波动的解析函数问题依照数学的观点可以归结为求解边界值问题。也即在流体波动内部存在着为某个函数必须满足的运动微分方程,在流体波动的边界上存在着为这个函数必须满足的边界条件。如果假定在均匀不变水深中沿正方向传播的表面波,其波动无旋,流体无黏性且不可压缩,则上述边界值问题的二维形式可写成[8]
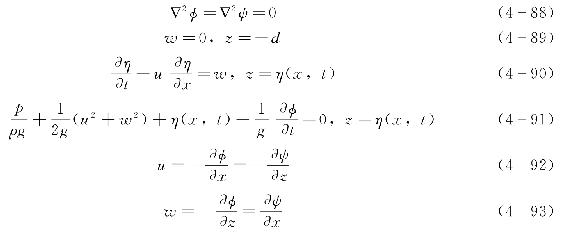
式中 φ——速度势函数;
ψ——流函数;
u、w——水质点速度的水平分量和垂直分量;
η(x,t)——波剖面;
p——压力;
ρ——水的质量密度;
g——重力加速度;
x、z——水平坐标和垂直坐标;
d——平均水深。
式(4-88)为φ或ψ所满足的运动微分方程,式(4-89)为底部边界条件,式(4-90)为运动学自由表面边界条件,式(4-91)为动力学自由表面边界条件。
4.5.2 求解过程
流函数的求解过程往往非常复杂,John.D.Fenton(1988)提出了一种无量纲化的流函数求解方法,从而极大地简化了流函数的求解过程[9]。首先将流函数求解中各几何变量和物理变量进行无量纲化转换,9个变量的名称和转化表达式如表4-4所示。
表4-4 变量的无量纲化表示
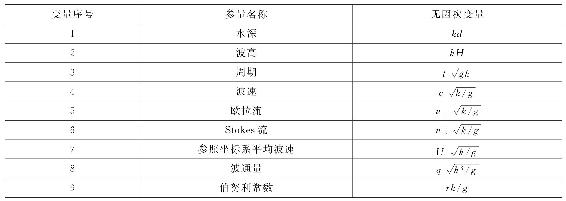
对于如图4-10所示的求解坐标系,波浪波动传播问题可视为一沿着海床水平的且不变形态的二维波浪波动,坐标系(x,y)的原点位于海底,波以速度c沿着x轴正向传播。设存在一移动速度为c的参照坐标系(X,Y),对于两个坐标系下的几何变量和速度变量存在关系式为

式中 t——时间;
u——静止坐标系下的水平速度;
v——静止坐标系下的竖向速度;
U——参照坐标系下的水平速度;
V——参照坐标系下的竖向速度。
为了完成问题的求解,所需要的方程数量和方程表达式如下:
(1)方程1。将无量纲的两个参数水深kd和波高(幅)kH通过波浪的波高与水深比值联系起来,建立的关系式是恒成立的,即

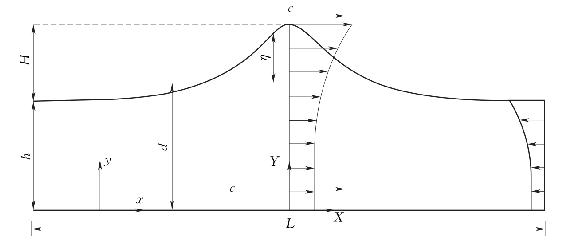
图4-10 流函数求解的坐标系
(2)方程2。该项包含了两个平行的方程,在求解时应根据所给具体条件来选取。当波浪周期已知时,将无量纲化的波高
kH与周期
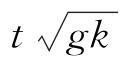
通过
H/
gt2
联系起来,表达式为
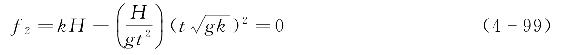
或者,当波长L已知时,将无量纲化的kH与H/L联系起来,可见

(3)方程3。通过定义
c=
L/
t,即波速等于波长除以周期,将波速
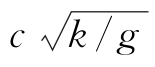
与周期
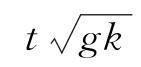
联系起来,则无量纲形式的方程表达式为
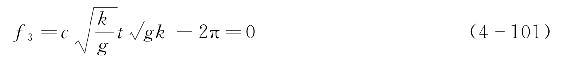
由于波速(https://www.daowen.com)
c事先未知,它取决于移动参照坐标系所依赖的速度,设参照坐标系下的平均水平流速为
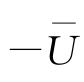
-,则在静止坐标系中时域平均速度可表达为

(4)方程4。当无水流时,
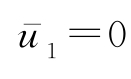
,
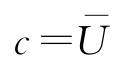
-。将上式各变量依据表4-4中无量纲化的参量表示为
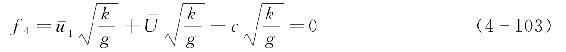
另一种情况下,若
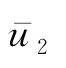
为静止坐标系下沿深度积分的平均流速,也即平均质量传输速度,而
Q为参照坐标系下的体积流量,则单位深度值为
Q/
d,从而存在关系式为

(5)方程5。同样地将上式各变量依据表4-4中无量纲化的参量并结合式
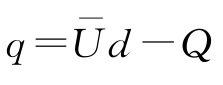
可表示为
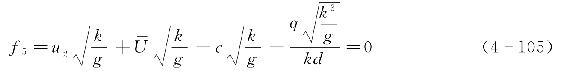
(6)方程6。当已知
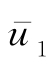
时,可以建立关系式为
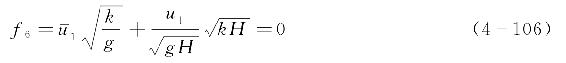
当已知
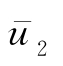
时,可以建立关系式为
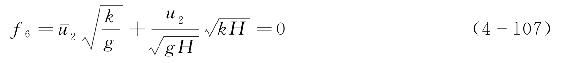
式(4-106)和式(4-107)是平行关系式,二者只选其一来计算。
以上方程是所有质点均需要满足的条件,以下两个方程式(方程7和方程8)将波面离散化成N+1个节点所得到的结果,其中N为傅里叶求解的阶数,如图4-11所示。
非线性波面边界条件在波面每一个节点处都应该满足,一个周期内波面共存在N+1个节点,这些计算节点应在波峰与波谷间水平均匀分布。这些点相对于平均水面的距离由ηm=η(xm),m=0,1,2,…,N来表示,其中η0表示波峰的相对高度,ηN表示波谷的相对高度。根据平均水位的定义可知波面各点相对距离的总和为零。
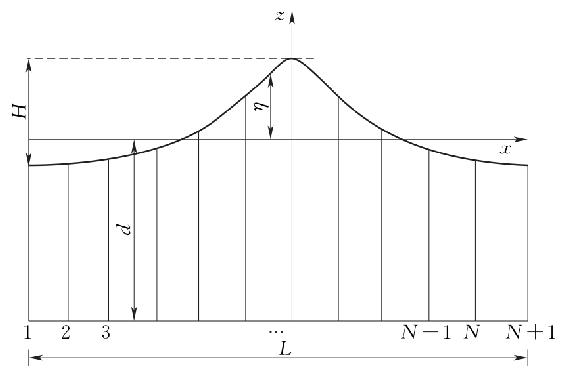
图4-11 离散化波面
(7)方程7。将波面各点上述特性进行归纳可表示为
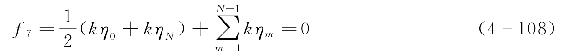
(8)方程8。波高等于波面中波峰与波谷之间的高度差,即H=η0-ηN,从而存在恒成立的表达式为

(9)方程9及其他方程。根据流体运动学边界条件,采用流函数在海底处的表达式和在水面处[Y=d+η(X)]的表达式,即

根据流体动力边界条件,采用流函数表达时应满足波面处为零,此时在自由表面处伯努利方程可表示为
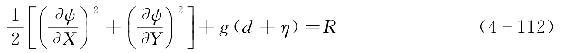
式中 R——常量。
符合式(4-110)~式(4-112)所有条件的流函数可设定为
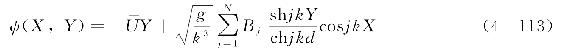
引入变量
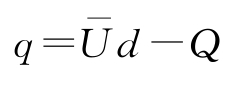
和
r=
R-gd后由式(4-111)和式(4-112)分别得到
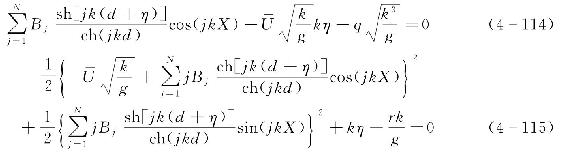
结合图4-11所示的波面分割点,运动学表面边界条件应该在N+1个节点上均适用。其中kXm=mπ/N(m=0,1,2,…,N),由式(4-114)进一步可得到
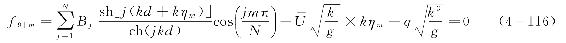
类似的,结合图4-11所示的波面分割点,动力学表面边界条件应该在N+1个节点上均适用。其中kXm=mπ/N(m=0,1,2,…,N),由式(4-115)进一步可得到方程式,即
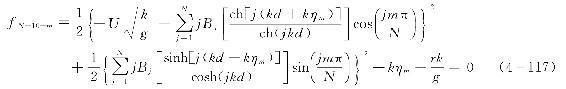
至此对于流函数的求解问题,上述方法共得到2N+10个方程,同时含有2N+10个未知量,故可以进行求解计算,最终得到表4-4中全部变量,同时可得到图4-11所示各点对应的kηj(j=0,1,2,…,N)值和系数Bj(j=0,1,2,…,N)。
4.5.3 最终变量转换
当选择流函数理论进行波浪分析后,需要得到不同位置、不同时刻的波面高度、波浪质点的水平速度、竖向速度和水平加速度、竖向加速度等变量结果。因为求解方法中采用了无量纲化处理,故上一部分中求得的未知量需要经过转化方能得到最终要求的波面高度、速度和加速度等量值。
在移动坐标系下,流函数与势函数的相互关系为

在移动坐标系中,变量X与静止坐标系下的x存在关系式为

结合式(4-113)和上述两式,势函数的表达式为
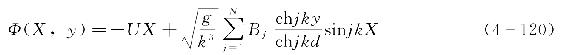
进一步可得到在静止坐标系下的势函数为
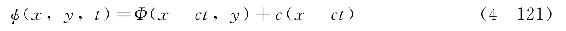
对于质点的水平速度u,可分别采用移动坐标系下的势函数和静止坐标系下的势函数来表达,由于针对的是同一个变量,故两种表示方法相等,进而有
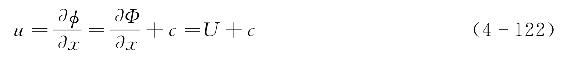
根据式(4-120)~式(4-122)可得
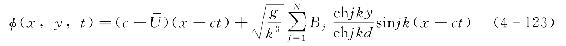
根据速度与势函数的导数关系,则水平向和竖向速度u和v的计算式分别为
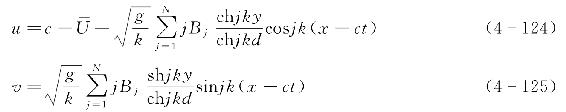
势函数φ(x,y,t)还存在关系式为

基于式(4-124)~式(4-126)可得到水平向和竖向加速度的表达式为
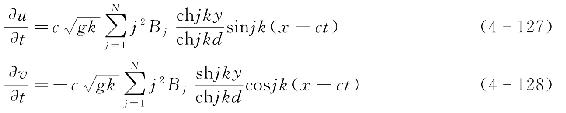
当已知波面各点对应的kηm(m=0,1,2,…,N)值后,可以结合快速傅里叶变换得到波面的表达式为
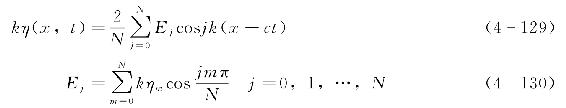
通过上述步骤,完成了基于2N+10个中间量求得不同时刻和位置处的波面高度、质点速度和加速度等变量,从而为进行海洋结构物波浪荷载计算提供了必要的基础。
