4.3 椭圆余弦波（Cnoidal波）

4.3 椭圆余弦波（Cnoidal波）

当波浪由深水区传至浅水区（0.05<d/L≤0.1）后，海底边界的摩擦阻力影响迅速增加，波高和波形将不断变化，波面在波峰附近变得很陡，而两波峰之间却相隔一段很长但又较平坦的水面，如图4-7所示。两波峰处的水质点运动特性与波动H/L的关系减弱，而与相对波高H/d的关系增强，即H/L和H/d都成为决定波动性质的主要因素。在这种浅水情况下，即使取很高的阶数，采用斯托克斯波理论仍不能达到所要求的精度。此时采用能反映H/L和H/d主要影响因素的椭圆余弦波理论来描述波浪运动，可以取得较为满意的结果。^［1］

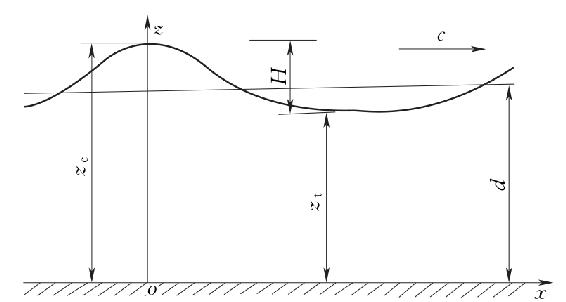
图4-7 椭圆余弦波波剖面、坐标系和相关变量

所谓椭圆余弦波是指水深较浅条件下的有限振幅、长周期波。它之所以称为椭圆余弦波，是由于波面高度η是用雅克比（Jacobian）椭圆余弦函数cn（）来表示。鉴于该理论求解的推导过程极为繁琐，本着工程应用的目的，在此直接给出该理论对应的主要计算结果。

4.3.1 积分模数

椭圆余弦波计算时最基本的变量为模数k。为了求解模数，首先应建立波浪要素（波长L、波高H、周期T）、水深d与椭圆积分模数k之间的关系。

波长L与模数k之间的关系为

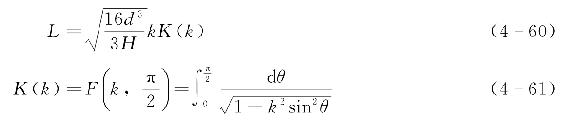
式中 K（k）——第一类完全椭圆积分；

k

——椭圆积分的模数，

。

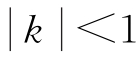
波浪的波速c与模数k的关系有两种形式，即

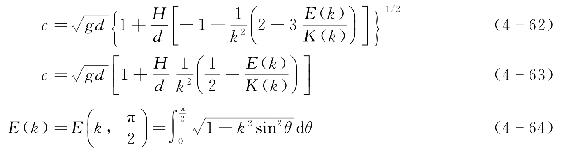
式中 E（k）——第二类完全椭圆积分。

根据波浪波速c、波长L和周期T的关系，即c=L/T，结合式（4-60）和式（4-62）或结合式（4-60）与式（4-63）可求得模数k，进而由式（4-60）求得波长。

4.3.2 特征参量的求解

在得到积分模数k和波长L变量后，可以依次求得椭圆余弦波对应的波浪诸特征参量，包括波面高度、速度与加速度等。

波峰距离海底的距离z_c为

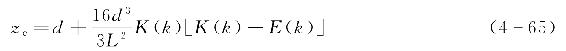
波峰与波谷距离相差一个波高H，则由上式可知，波谷距离海底的距离z_t为

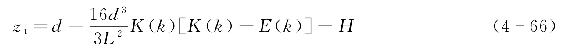
海底以上的波面高度z_s与波谷至海底距离z_t的关系为

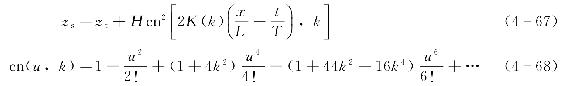
式中 cn（u，k）——雅克比椭圆余弦函数。

将式（4-66）代入式（4-67）后，得到任一相位x和时刻t下海底以上的波面高度z_s为

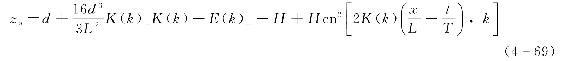
静水面以上的波面高度η为

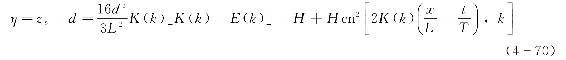
波动场内任意点（x，z）处水质点的水平向与竖向速度u_x、u_z分别为

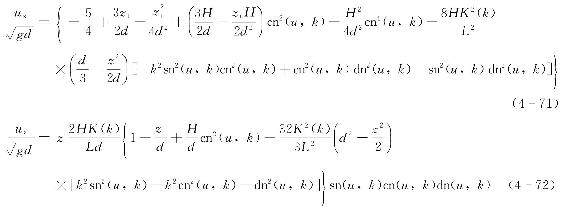
式（4-71）、式（4-72）中，函数sn（u，k）为雅克比椭圆正弦函数，cn（u，k）为雅克比椭圆余弦函数，dn（u，k）为雅克比椭圆德尔塔（Delta）函数，3个函数的自变量u为

雅克比椭圆正弦函数、余弦函数和德尔塔函数存在关系式为

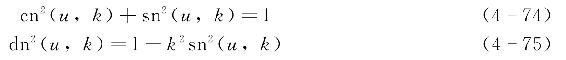
根据式（4-68）可求得雅克比椭圆余弦函数值，结合式（4-74）和式（4-75）可以求得对应的椭圆正弦函数和椭圆德尔塔函数值。

波动场内任意点（x，z）处水质点的水平向与竖向加速度a_x、a_z分别为

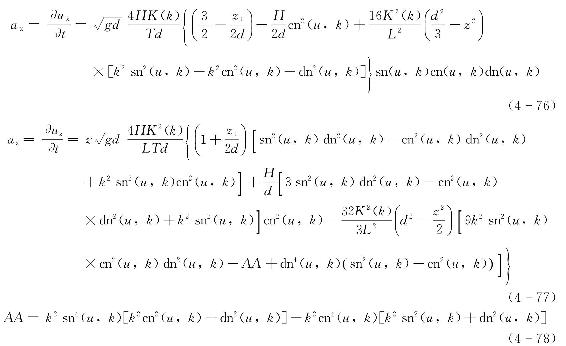
式（4-78）表示的变量AA为式（4-77）所包含的中间变量。

4.3.3 极限情形

对于椭圆余弦波，当模数取极值

k

=0时，根据式（4-61）和式（4-64）可得，

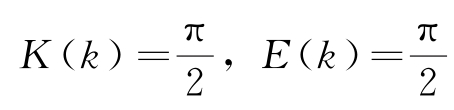
。将

k

=0代入式（4-68）后得到，cn（

u

，0）=cos（

u

），此时椭圆函数变成了三角函数。结合上述关系代入式（4-67）和式（4-70）后得到

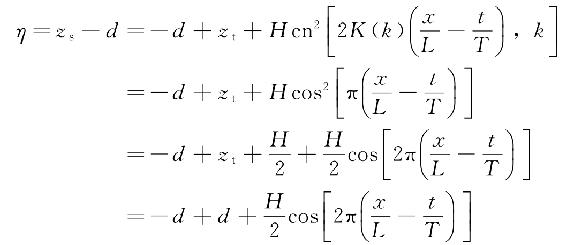
线性波的波面高度计算式，即式（4-21）可表达为

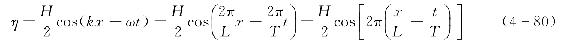
式（4-79）与式（4-80）相同。由此可见，线性波就是椭圆余弦波当模数k=0时的一种特殊情况。

同样可以证明孤立波就是椭圆余弦波当模数k=1时的另一种特殊情形。