4.3.2 饱和至非饱和状态下植被根系生态加固土的广义弹塑性模型
1)应变构成与分解:应变增量分为弹性应变和黏塑性/塑性应变
2)弹性方程:
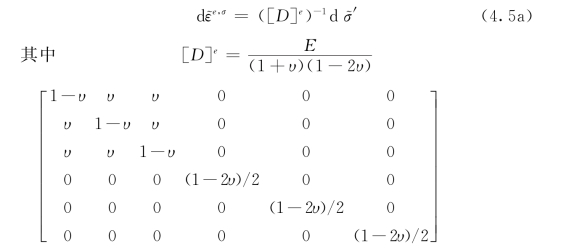
E和υ分别为弹性模型常数。
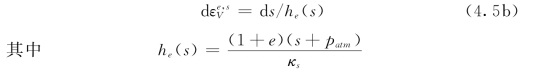
式中:κs为吸力小于s 0的压缩指数；p atm为大气压力。
3)塑性方程:
应力屈服以后,塑性应变可以写成
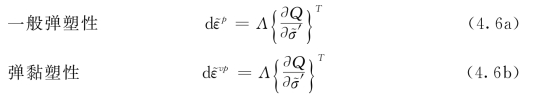
非饱和土对应吸力的塑性应变
式中:Λ为塑性应变乘子；Q为塑性势函数。当s-s 0＞0时,
大于s0的压缩指数。
4)屈服面函数和相关联流动势面函数:
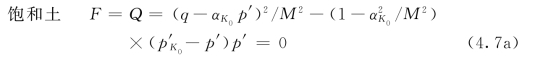
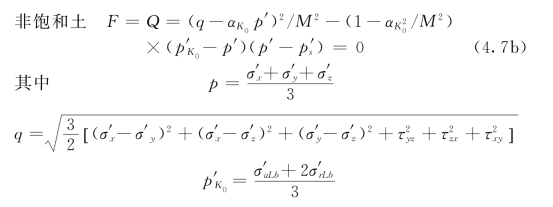
式中:αK 0为表征各向异性程度的参数(各向异性线AL的坡度)；M为临界状态应力比；p′s为表征吸力影响的状态参数；σ′aLb、σ′rLb分别为饱和土的,未考虑黏滞性、根系固土特性、结构性的、非饱和特性或吸力作用时的初始竖向和横向屈服应力。
5)当考虑黏滞性影响时,由于先期固结压力随塑性体应变的增加而增加(图4.1),竖向和横向初始屈服应力分别为
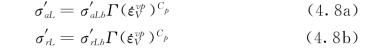
图4.1 屈服应力随塑性体应变率的增加而扩大(Kim和Leroueil[126],2001)
6)当考虑结构性影响时,由于胶结强度致使抗剪强度提高,竖向和横向初始屈服应力分别为
或者以另一种数学形式表示为
式中:σc为胶结强度；bσ为破损指数。
破损土的压缩曲线可以看作是一组从结构性原状样到重塑样的具有不同先期固结压力的等值线,如图4.2所示。
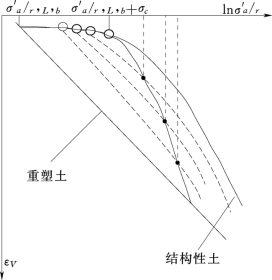
图4.2 先期固结压力不断减小的结构性土的破损过程
7)当考虑非饱和特性影响时,由于吸力增加,竖向和横向初始屈服应力分别相应增加(图4.3),其中e w=esr。
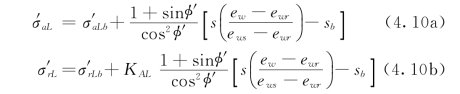
8)当考虑根系固土作用特性时,由于抗剪强度的增加,竖向和横向初始屈服应力分别如式(4.1)和式(4.3)所示。
9)硬化规律:
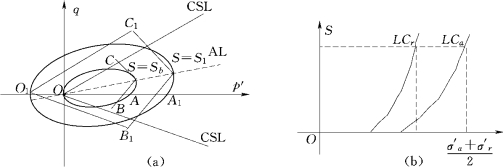
图4.3 非饱和土的屈服面随吸力增加而扩大
(a)椭圆屈服面随吸力增加而扩大；(b)横向和竖向先期固结压力随吸力增加而增大
特别地,对于非饱和土(图4.4)
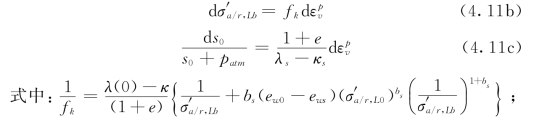
bs是饱和指数,它可以控制不同吸力作用下非饱和土趋近于饱和土的程度,不同应力状态下饱和土与非饱和土压缩曲线之间的距离；k(s)
示于图4.4。
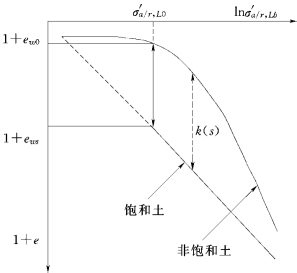
图4.4 与饱和土的压缩曲线相联系的非饱和土的压缩曲线
这样,沿用常规的建模方法便可以建立饱和至非饱和状态下植被根系生态加固土的广义弹塑性模型。