7.5 植被防护土坡的近似解析计算和分析
某边坡(约18m厚)进行过超过1年的蠕动变形量测[52,72](Samtani和Desai,1996；Cristescu等,2002),滑移形态从下往上基本可以分为3个主要分层:无滑移层(约1m厚)、剪切流动层(约5m厚)和刚性体滑移层(约12m厚)。坡土的天然容重γ=21.85k N/m3,土坡高度h=18m,初始参照时间t 0=1d,土坡倾角β=14°。其余计算参数参照文献[71～72]中参数值并通过反演分析得到。在反演分析时,保证计算位移分布形态满足观测到的3个主要分层:无滑移层(约1m厚即滑移区分层高度h 1=1m)、剪切流动层(约5m厚即h 2=6m)以及刚性体滑移层(约12m厚)。计算参数列于表7.3中。根据式(6.14)可以计算出土坡渐进变形理论解析值,并和148d、196d、260d、356d 4个时间段的观测位移数据一起示于图7.11中。
表7.3 模型计算参数
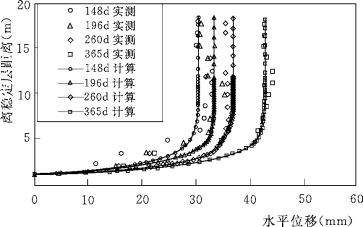
图7.11 某天然土坡观测位移沿深度分布和理论解析值比较图
从图7.11可以发现,坡体的滑移形态从下往上基本呈现稳定层、剪切层和随动层3个主要分层,且实测结果与理论值较为一致。
通过参数分析,图7.12～图7.16给出了边坡的渐进变形随着各向异性参数αK 0、粘滞性参数ψ0、根系固土强度参数μ0、结构破损度D以及广义吸力S的变化关系。
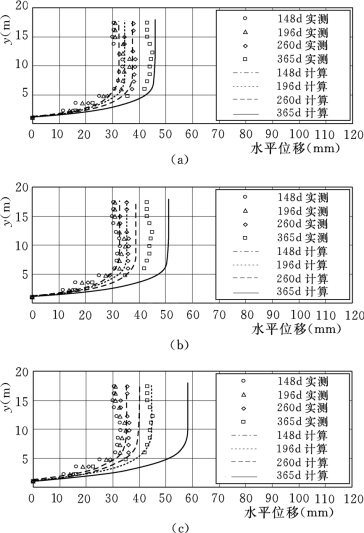
图7.12 某天然土坡观测位移沿深度分布和理论解析值比较图(不同黏滞性参数ψ0/V 0)
(a)0.002；(b)0.0025；(c)0.003
从图7.12～图7.16中还可以看出,边坡的渐进变形随着各向异性参数αK 0的减小、或黏滞性参数ψ0的减小、或根系固土强度参数μ0的减小、或结构破损度D的增大以及广义吸力S的减小而增大。
利用下列参数λ=0.079、κ=0.018、OCR=1、M 0=1.243、M 1=1.143、K oc0=0.5及K NC0=0.5,根据式(6.34)可以得出Su/σ′z随初始裂隙发育程度参数或根系固土作用参数μ0、各向异性参数αK 0、破损比D、与应力路径相关的Lode角θ、及塑性体应变率变化的关系,如图7.17～图7.21所示。
可以看出,天然坡土渐进破损的归一化不排水抗剪强度Su/σ′z随着初始裂隙发育程度参数μ0的增加(根系固土作用使初始裂隙数量减少)而增大,随着各向异性参数αK 0的增加而增大,随着塑性体应变率的增加而增大,随着破损比D(表征次生裂隙影响)和Lode角θ的增大而减小。
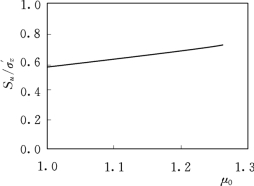
图7.17 在θ=-30°时归一化不排水强度与裂隙发育程度参数或根系固土作用参数μ0在各向异性参数αK 0=0.75、破损比D=0.4时的关系曲线
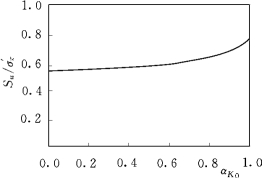
图7.18 在θ=-30°时归一化不排水强度与各向异性参数αK 0在破损比D=0.4时的关系曲线
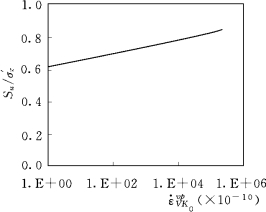
图7.19 归一化不排水强度与塑性体应变率˙ε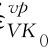
在αK 0=0.75、D=0.4和Lode角θ=-30°时的关系曲线
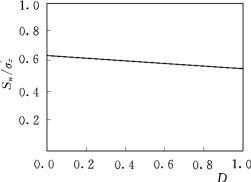
图7.20 在θ=-30°时归一化不排水强度与破损比D在各向异性参数αK 0=0.75时的关系曲线
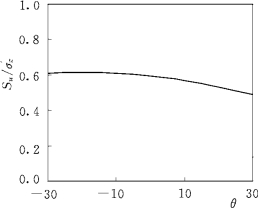
图7.21 归一化不排水强度与Lode角θ在αK 0=0.75和D=0.4时的关系曲线