6.5 植被防护土坡的近似强度解析模型
土坡面层由于长期经受风力和水力侵蚀、湿胀干缩、热胀冷缩等的作用,因此往往会在面层和土坡内部引起许多裂隙。一般认为土中的裂隙是由于拉应力大于土的抗拉强度造成的,但从广义结构性的角度看,在荷载的作用下,土的结构破损先从较弱的胶结面开始,然后是胶结致密的团粒或土块开始破碎,直到所有团粒或土块均被破坏,土表现出重塑土的特征,这也为许多试验结果所证实。从结构性黏土的应力应变曲线中可以发现,从天然土到重塑土的过程基本上可以划分为三个阶段:第一阶段基本上是弹性变形,可以认为土的结构性保持完好,为结构初步调整阶段,土的内部还没出现裂隙；第二阶段的变形大大增加,说明变形不仅仅是由颗粒位置调整或滑移产生的,还应包括结构破损、拉裂或剪切破坏产生的裂隙、局部应变促成的剪切带的形成等因素引起的变形,换言之,土团或土块已经被四分五裂,土的内部已经布满了大大小小的裂隙；第三阶段结构性土的应力应变曲线渐渐趋近于重塑土的曲线,可以认为裂隙进一步发展到细部层次,即颗粒之间的紧密联结已经基本破坏完毕,土颗粒的滑移已成为塑性变形的主要原因。
那么,在裂隙产生和发展过程中,坡土的强度是如何变化的呢?为了探究裂隙对坡土强度的影响,可以利用各向异性天然结构性土的屈服面函数推导出土的渐进破损归一化不排水强度的解析表达式,研究土的渐进破损归一化不排水强度与裂隙发育程度、各向异性、黏滞性、应力路径等因素的相关性。
屈服面函数为:
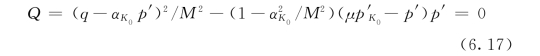
其中裂隙发育程度参数μ0用来表征初始裂隙的影响(考虑根系固土作用特性,根系固土作用使初始裂隙数量减少),M=6sinφ′/(3-sinφ′)是η的临界状态值[这里η=q/p′,q=
偏应力sij=σ′ij-p′δij,σ′ij是有效应力张量,p′=σ′kk/3是平均有效应力；这里δij是Kronecker delta变量]。同时引入损伤变量D(表征次生裂隙影响)以及无破损状态和完全破损状态下的临界状态强度比M 0、M 1,并且M=M 0-D(M 0-M 1)。为了可以考虑加荷路径和一般应力条件,模型一般应用Mises屈服破坏准则、Mohr-Coulomb屈服破坏准则、Matsuoka屈服破坏准则或Lade屈服破坏准则建立在三维应力空间。如果采用显式形函数g(φ′,θ)的形式,非对称的屈服面函数可以写成:
基于Potts和Zdravkovic[236]的思路,可以得到从天然土到裂隙土的渐进破损状态下考虑多种因素的不排水强度Su的表达式[139](Zhou,2006)。首先有
式中:下标“ds”表示破损状态(destructuration state)的意思。
由图6.3可得
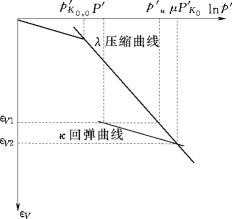
图6.3 初始固结与回弹曲线
定义OCR=σ′v,max/σ′vi,这里σ′v,max是土单元历史上曾受到的最大应力。从而有
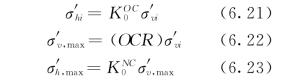
式中:K 0 NC为正常固结状态下的静止土压力系数。
利用式(6.22)和式(6.23)可以得到qi和p′i
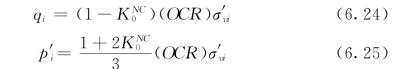
由于与σ′v,max、σ′h,max、qi和p′i相关的应力状态为正常固结状态,利用式(6.18)式可得到:
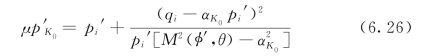
根据Kim和Leroueil(2001)[126]关于先期固结压力(屈服应力)随塑性体应变率的增加而增大的研究结果(图4.1),我们假定
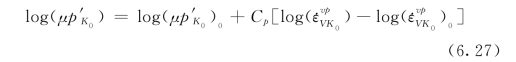
式中:˙ε
、(˙ε
)0、Cp分别为实际塑性体积应变率、参照塑性体积应变率(黏滞性极低)和先期固结压力随塑性体应变率的增加而增大的比例系数。
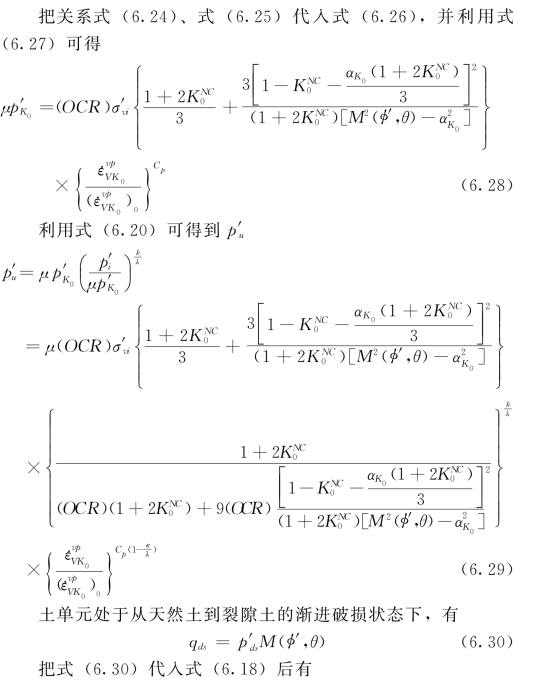
联合式(6.20)和式(6.31)得到
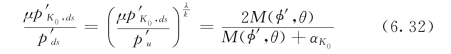
进而有
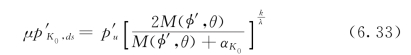
利用上述推导得到的一系列关系式(6.19)、式(6.29)、式(6.30)、式(6.31)和式(6.33),最终可以得到
