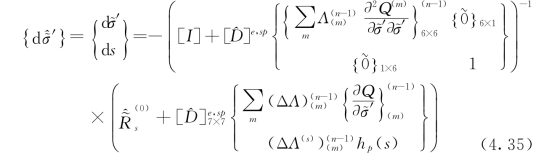4.4.4 饱和土与非饱和土的广义隐式数值积分格式
在模型的数值分析应用中,饱和土模型的数值积分无论是显式算法还是隐式算法都已比较成熟,但非饱和土则因吸力的存在而难度相对增加,这是因为模型中的屈服函数、塑性势函数、硬化定律等都和吸力相关。目前比较成熟的关于非饱和土模型数值积分的显式算法和隐式算法主要以Sheng等(2003)[227]和Vaunat等(2000)[228]为代表。前者把吸力增量作为一种应变增量的形式,从而可以借鉴饱和土的显式积分算法,但显而易见这改变了吸力作为与净应力同等重要的应力变量的物理含义。后者则把吸力仍然作为应力变量,但需形成一个广义的应力应变系统以形成隐式算法需要的刚度方阵,而且在借鉴饱和土的隐式算法时积分迭代计算要不时地交替进行,以保证最终的应力状态位于吸力确定的屈服面上。这两个模型算法都较好地对巴塞罗纳模型实现了数值积分收敛,从而验证了模型并确保了其在数值分析中的应用。为了建立饱和土与非饱和土的广义隐式数值积分格式,把吸力作为一种形式的“应变”,但是其物理意义上仍然扮演着与净应力类似的应力变量的作用。
1)广义应力应变增量形式矢量定义为
 (https://www.daowen.com)
(https://www.daowen.com)

作为一种形式的“应变”,d s=d se+d sp,其中d se和d sp分别是吸力增量的弹性和塑性分量。这样,本构方程就可以表现为纯应变驱动的形式,从而可以借用饱和土的数值积分格式来计算非饱和土的应力应变发展过程,构建统一的饱和土与非饱和土的广义隐式数值积分格式。
4)塑性应变乘子更新。对于每个屈服面函数


对式(4.30)微分,可以得到下列矢量方程(需要注意的是,吸力作为一种形式的“应变”,但是在物理意义上它仍然扮演着与净应力类似的应力变量的作用)。

当最终应力满足了更新后的应力屈服准则以后,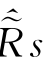 应当减小直至为零。试算弹性应力t+Δt
应当减小直至为零。试算弹性应力t+Δt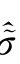 ′tr保持不变,Taylor展式代入式(4.33),并且考虑d sp=(Λ(s))h p(s),便可以产生一个新的
′tr保持不变,Taylor展式代入式(4.33),并且考虑d sp=(Λ(s))h p(s),便可以产生一个新的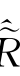 s(n)
s(n)
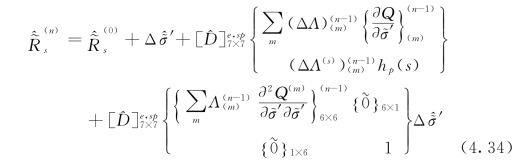
式中:Δ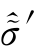 为广义应力
为广义应力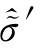 的增量;ΔΛ
的增量;ΔΛ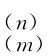 为对应净应力的塑性乘子Λ(m)的增量;ΔΛ(s)为对应吸力的塑性乘子Λ(s)的增量。令
为对应净应力的塑性乘子Λ(m)的增量;ΔΛ(s)为对应吸力的塑性乘子Λ(s)的增量。令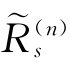 为0,将得到更新后的广义应力增量
为0,将得到更新后的广义应力增量