6.4 植被防护土坡变形的近似解析模型和方法
在土坡的蠕变变形过程中,速度V是一个不可逆的变量[72,75](Cristescu等,2002；Zhou,2007),因此速度变量可以与黏塑性应变建立下列关系
假定图6.1(x、y)坐标系中沿x方向(坡度β方向)的速度矢只是深度的函数,即V x=V(y),V y=V z=0,因此有:
这里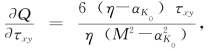
把式(6.9)、式(6.10)、式(6.11)中各应力分量的表达式代入式(6.12)后可得
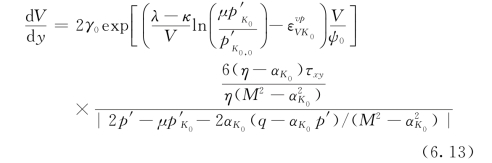
把式(6.13)进行积分,同时假定“稳定层”与“剪切层”交界处无滑移,即V|y=h1=0,得到土坡滑移区渐进变形的速度场为
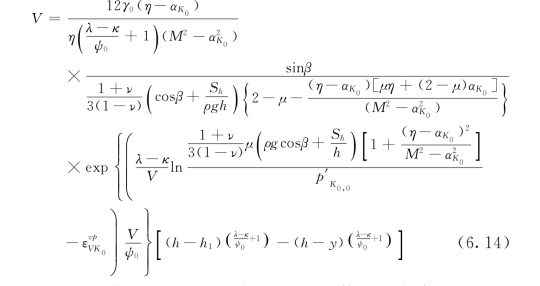
可以看出式(6.14)是坐标y的幂函数,速度将随y的增大逐渐趋向于一个稳定值[表现为y≥h 2的土层随“剪切层”(h 2≥y≥h 1)一起刚性滑动,该土层可以称为“随动层”]。整个滑移区从下往上可以划分为3个主要分层:土坡稳定层(h 1≥y≥0)、剪切层(h 2≥y≥h 1)和随动层(y≥h 2),如图6.2所示。
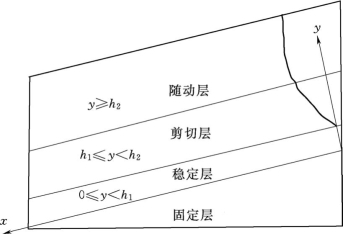
图6.2 天然土坡滑移模式分布示意图
另外,根据6.2章模型部分给定的两个限定条件,即结构初始临界破损后才有黏塑性变形发生,即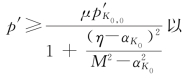
及在临界状态下产生有限的黏塑性体积变形,即p′K 0≤
把限定条件表示成坐标y的函数,也可以知道在整个滑移区主要存在着h 1和h 2两个分区高度,使0≤y≤h 1层内基本无黏塑性变形(无滑移,可以认为该层是“稳定层”),而在h 1≤y＜h 2层内产生主要的黏塑性变形(剪切滑移,可以认为该层是“剪切层”)。其实,由于天然沉积过程中上覆压力的不同,土坡不同埋深的土的结构初始破损强度μp′K 0,0是不同的,利用不同位置p′K
的临界条件,可以在
应力分布曲线上近似确定破损变形区分布范围。
在利用式(6.14)求解滑移区的速度场时,需要随时更新不同时刻模型中的黏塑性体应变。在初始时刻t=t 0的黏塑性应变假定为:
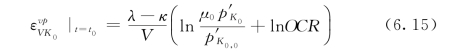
则在任意时刻t=te的黏塑性应变可以写为:
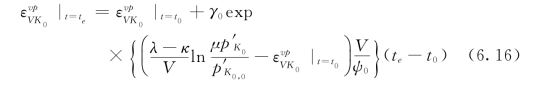
利用式(6.14),可以很方便地利用Office系统中的Excel通用软件公式功能,求解土坡滑移区的速度随坡土深度的变化关系。然后乘以时间间隔,便可以得到土坡渐进变形的大小。