6.2 饱和状态下植被根系生态加固土的广义弹黏塑性模型
为了描述土的渐进变形破坏特性,先建立一个考虑各向异性、黏滞性、结构性的弹黏塑性模型。
式中:˙εij、˙ε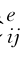
、˙ε
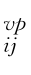和˙s ij(i=1,2,3；j=1,2,3)分别为总应变率、弹性应变率、黏塑性应变率和偏应力率；S和
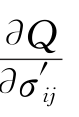分别规定了黏塑性应变的大小和方向；σ′ij和p′分别为有效应力和球应力；κ和G为弹性模型参数；V=1+e 0,为初始比容。
黏塑性流动面函数可以写为:
曾有人对世界范围内40多种天然黏土进行研究,发现土的屈服面都表现出强烈的各向异性,例如K 0加载条件下的屈服应力是各向同性加载的1.6倍[112～113](Leroueil和Vaughan,1990；Diaz-Rodriguez等,1992),为此引入αK 0用来定义结构性土黏塑性流动面Q的初始倾度来考虑初始各向异性,αK 0≈
为了考虑根系固土作用特性,引入μp′K 0用来定义结构性土黏塑性流动面Q的大小。同时引入损伤变量D以及无破损状态和完全破损状态下的临界状态强度比M 0、M 1,其中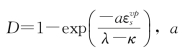
为定义损伤变量的模型参数,λ、κ分别是正常固结土的初始压缩指数和回弹指数；
是η的临界状态值[这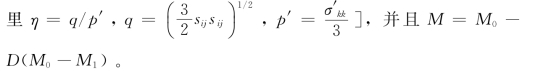
假定存在一个“弹性核”,只有超出其范围才会发生黏塑性应变和破损变形。利用式(6.3),可以判断当平均有效应力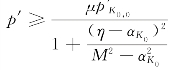
,将会发生黏塑性应变和破损变形。这里μp′K 0,0定义了该“弹性核”(在p′～q平面内为结构初始破损的临界黏塑性流动面)的大小。
下面简要介绍一下规定黏塑性应变大小的S的求法。黏塑性体应变可以写为:
式(6.2)、式(6.3)、式(6.6)和式(6.7)式构成了弹黏塑性本构方程。整个模型中ψ0/V和t 0是通过K 0固结仪流变试验得到的模型参数；λ/V、p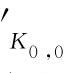
(在压缩曲线上对应有体应变εVK 0,0)是用于定义模型中λ线的位置和倾角的参数,其中p
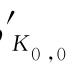还给定了“结构初始破损的临界黏塑性流动面”的大小；式(6.7)中ε
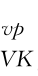0是实际累积黏塑性体应变,它实际上担当了类似于剑桥模型中硬化参数的作用。值得注意的是,ε
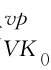可以利用式(6.6)逐步积分求得,其值小于或等于ε
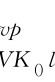,以便描述流变随时间渐进终止的变形特性；ε
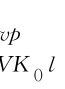是K 0压缩条件下的极限黏塑性体应变