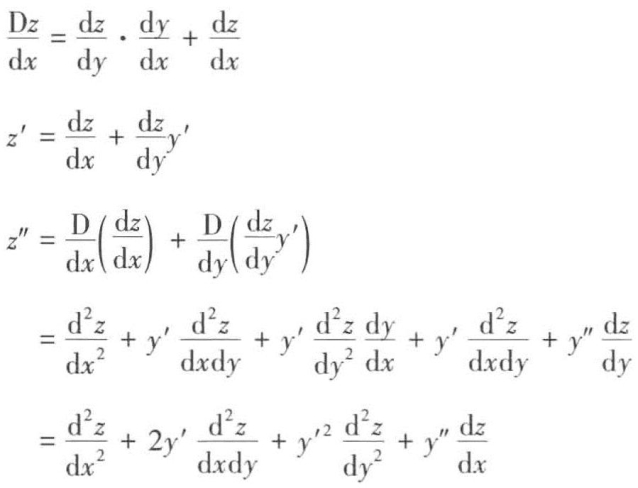[数学]
[160](https://www.daowen.com)
关于现实世界中数学上的无限之原型144
Ⅰ
加在第17—18页上[30]:思维和存在的一致。——数学上的无限
我们的主观思维和客观世界遵循同一些规律,因而两者的结果最终不能互相矛盾,而必须彼此一致,这个事实绝对地支配着我们的整个理论思维。这个事实是我们理论思维的不以意识为转移的和无条件的前提。18世纪的唯物主义,由于它的本质上形而上学的性质,只是从内容方面研究这个前提。它只限于证明一切思维和知识的内容都应当来源于感性的经验,并且重新提出下面这个命题:感觉中未曾有过的东西,理智中也不存在145。只有现代的唯心主义的、同时也是辩证的哲学,特别是黑格尔,才又从形式方面研究了这个前提。尽管我们在这里遇到无数的任意虚构和凭空臆造,尽管这种哲学的结果——思维和存在的统一——采取了唯心主义的头足倒置的形式,可是不容否认,这种哲学在许多场合下和在极不相同的领域中证明了思维过程同自然过程和历史过程是类似的,反过来也一样,并且证明了同一些规律对所有这些过程都是适用的。另一方面,现代自然科学已经把一切思维内容都来源于经验这一命题以某种方式加以扩展,以致把这个命题的旧的形而上学的限制和表述完全抛弃了。它由于承认了获得性状的遗传,便把经验的主体从个体扩大到类;每一个体都必须亲自取得经验,这不再是必要的了,个体的个别经验在某种程度上可以由个体的历代祖先的经验的结果来代替。例如,在我们中间,一些数学公理对每个八岁的儿童来说都好像是不言自明的,用不着通过经验来证明,这只是“累积的遗传”的结果。想用证明的方法向一个布须曼人或澳大利亚黑人传授这些公理,这可能是困难的。
在本书中[31],辩证法被看做关于一切运动的最普遍的规律的科学。这就是说,辩证法的规律无论对自然界中和人类历史中的运动,还是对思维的运动,都必定是同样适用的。一个这样的规律可以在这三个领域中的两个领域中,甚至在所有三个领域中被认识到,只有形而上学的懒汉才不明白他所认识到的是同一个规律。
让我们举一个例子。在一切理论进展中,同17世纪下半叶发明微积分比较起来,未必再有别的东西会被看做人的精神如此崇高的胜利。如果说在什么地方可以出现人的精神的纯粹的和唯一的业绩,那就正是在这里。至今仍围绕着微积分中所运用的各种数量(各阶的微分和无限)的那种奥秘,是下述事实的最好的证据:人们总是以为,这里所研究的是人的精神的纯粹的“自由创造物和想象物”[32],而客观世界提供不出任何相应的东西。然而实际情形恰恰相反。自然界对这一切想象的量都提供了样本。
我们的几何学是从空间关系出发,我们的算术和代数学是从数量出发,这些数量是同我们的地球上的各种关系相适应的,就是说,是同力学称之为质量的物体大小相适应的,这些质量是出现在地球上并由人使之运动的。和这些质量比起来,地球的质量显得是无限大的,并且也被地球上的力学当做无限大来看待。地球半径=∞,这是整个力学在考察落体定律时的原则。但是,当我们所考察的是那些用天文望远镜才能观察到的恒星系中的、必须以光年来估算的距离时,不只是地球,而且整个太阳系以及其中呈现出的各种距离,又都成为无限小了。这样,我们在这里不仅已经有了第一阶的无限,而且还有了第二阶的无限,我们的读者高兴的话,还可以凭自己的想象构造出无限空间里的其他的更高阶的无限。
但是,按照现在物理学和化学中流行的观点,力学所研究的地球上的质量,即物体,都是由分子构成的,而分子是最小的微粒,如果不破坏所研究的物体的物理的和化学的同一性,便不能再加以分割。根据威·汤姆生的计算,最小的分子的直径不能小于五千万分之一毫米146。但是,即使我们假定最大的分子的直径甚至达到二千五百万分之一毫米,那么,同力学、物理学、甚至化学所研究的最小的质量比较起来,分子仍然是一个非常微小的量。尽管如此,分子还是具有所考察的质量的一切特性,可以在物理学上和化学上代表质量,而且在一切化学方程式中确实代表着质量。一句话,分子同相应的质量相比具有完全相同的特性,正如数学上的微分同其变数相比具有完全相同的特性一样。唯一的差别是:在微分中,在数学的抽象中,在我们看来似乎是神秘的和无法解释的东西,在这里却是不言自明的,并且可以说是一目了然的。
自然界使用这些微分即分子的方式和所遵循的规律,与数学使用数学中的抽象的微分的方式和规律是完全相同的。例如:x3的微分是3x2dx,这里略去了3xdx2和dx3。如果我们按几何学来设想,我们就可以得到一个边长为x的立方体,其边长按无限小dx量增大。我们假定这一立方体是由一种可升华的元素构成的,比方说,是由硫磺构成的;再假定构成一个角的三面被遮盖起来,另三面是露着的。我们把这个硫磺立方体放在硫磺蒸气中,再把气体温度降低足够的度数,于是硫磺蒸气就凝结在这个立方体的露着的三面上。如果我们设想这是一个以纯粹的状态发生的过程,因而假定在这三面的每一面上最初凝结了一个分子厚的一层,那么我们就完全没有超出物理学和化学惯用的实验方法。立方体各边的长度x增大了一个分子直径的长度dx。立方体的容积x3增加了x3和x3+3x2dx+3xdx2+dx3之差,按照数学中的同一理由,我们可以略去dx3和3xdx2,即略去一个分子和联成直线的长度为x+dx的三排分子。结果是一样的:这个立方体的质量增加了3x2dx。
严格说来,硫磺立方体上并不存在dx3和3xdx2,因为在同一空间内不能有两个或三个分子存在,因而这个立方体的质量的增量恰好是3x2dx+3xdx+dx。这可以由下述事实来说明:在数学上dx是一个线性量,而大家知道,这种没有厚和宽的线在自然界中并不能独立地存在,因此数学的抽象也只是在纯数学中才是无条件地有效的。既然这个3xdx2+dx3也可以略去,所以也就没有什么差别了。
蒸气的情形也是一样,如果一杯水的最上面的一层分子蒸发了,那么水层的高度x就减少了dx,这样一层分子又一层分子地蒸发下去,事实上就是一个连续的微分。如果热的水蒸气在一个容器中由于压力和冷却又凝结成水,而且分子一层又一层地累积起来(在这里,我们必须把那些使过程变得不纯粹的次要情况撇开不谈),直到容器满了为止,那么这里就不折不扣地发生了一种积分,这种积分和数学上的积分不同的地方只在于:一种是由人的头脑有意识地完成的,另一种是由自然界无意识地完成的。不过,和微积分运算完全类似的过程,不仅仅发生在从液态到气态或从气态到液态的转变中。当物体运动由于碰撞而中止,并转化为热即分子运动的时候,那么这不是物体运动发生微分,又是什么呢?当水蒸气的分子运动在蒸汽机的汽缸中累积起来,把活塞冲高一定的距离并且自身转化为物体运动的时候,这种运动不是被积分了吗?化学把分子分解为原子,即具有更小的质量和空间广延的量,然而是同阶的量,所以二者相互间保持一定的、有限的比值。因此,表示物体的分子组合的一切化学方程式,就形式来说是微分方程式。但是这些方程式由于其中所表示的原子量实际上已经积分化了。化学所计算的正是量的相互关系为已知的微分。
但是,原子决不能被看做单一的东西或者被笼统看做已知的最小的物质粒子。撇开越来越倾向于把原子看做复合的东西的化学本身不谈,大多数物理学家都断言:充当光辐射和热辐射的介质的宇宙以太33,同样是由分立的粒子构成的,不过这些粒子极小,以致它们同化学的原子和物理的分子的关系就像后两者同力学上质量的关系一样,也就是像d2x同dx的关系一样。因此,这里我们在现今流行的关于物质构造的观念中,同样看到了二阶微分;每个人只要高兴,完全有理由设想:自然界中一定还存在着和d3x、d4x等等相似的各种情况。
因此,不论人们对物质构造采取什么样的观点,下面这一点是十分肯定的:物质按质量的相对的大小分成一系列大的、界限分明的组,每一组的各个成员在质量上各有一定的、有限的比值,但相对于邻近的组的各个成员则具有数学意义上的无限大或无限小的比值。目力所及的恒星系,太阳系,地球上的物体,分子和原子,最后,以太粒子,都各自形成这样的一组。这种情况不会因为我们在各组之间发现中间成员而有所改变。例如,在太阳系的物体和地球上的物体之间有小行星,其中一些小行星的直径并不比罗伊斯幼系公国147的直径大些,此外还有流星等等。例如,在地球上的物体和分子之间有有机界中的细胞。这些中间成员只是证明:自然界中没有飞跃,正是因为自然界全是由飞跃所组成的。
数学计算的只要是实数,它就也要毫不犹豫地采用这个观点。对地球上的力学说来,地球的质量已经被看做无限大,而在天文学中,地球上的物体及与之相当的流星却被看做无限小,同样,对于天文学来说,只要它超出最邻近的恒星的范围来研究我们这一恒星系的构造,太阳系诸行星的距离和质量就会趋近于零。但是,数学家一旦退入他们的无法攻克的抽象堡垒,即所谓纯数学,这一切相似就都被忘却,无限就变成完全神秘的东西,而在分析中所运用的方式方法就好像成了完全不可理解的、同一切经验和一切理智相矛盾的东西。数学家们的这种处理方法令人奇怪地总是取得正确的结果,他们对这种方法与其说作说明不如说作辩解时所表现的愚蠢和荒唐,超过了例如黑格尔自然哲学的各种最坏的虚虚实实的幻想,然而面对这些幻想,数学家们和自然科学家们却害怕得难以言状。他们谴责黑格尔把抽象推到了极端,可是他们自己正是这样做的,而且规模还大得多。他们忘记了:全部所谓纯数学都是研究抽象的,它的一切数量严格说来都是想象的数量,一切抽象推到极端都变成荒谬或走向自己的反面。数学的无限是从现实中借用的,尽管是不自觉地借用的,所以它只能从现实来说明,而不能从它自身、从数学的抽象来说明。如果我们从这方面来研究现实,那么如我们看到的,我们就会发现作为数学的无限性关系的来源的现实关系,甚至会发现自然界中使这种关系起作用的数学方法的类似物。而这样一来,事情就得到了说明。(海克尔对思维和存在的同一性的糟糕的复述。但是还有连续的物质和分立的物质之间的矛盾,见黑格尔。)148
[18]
数学上的所谓公理,是数学需要用做自己的出发点的少数思维规定。数学是数量的科学;它从数量概念出发。它以不充分的方式给数量下定义,然后把这个定义中没有包含进来的数量的其他一些基本规定性,当做公理从外部补充进来,在这里,这些规定性表现为未经证明的东西,自然也是数学上无法证明的东西。对数量的分析会得出所有这些公理的规定,即数量的必然规定。斯宾塞说得对:我们所认为的这些公理的不证自明性是传承下来的。这些公理只要不是纯粹的同义反复,都是可以辩证地证明的。
[66]
同一和差异——在微分学中已经存在辩证的关系,在那里,dx是无限小,然而是起作用的并且是无所不能的。
[67]
数学问题。看来,没有什么东西比四则运算(一切数学的要素)的差异具有更牢固的基础了。然而,乘法一开始就表现为一定数目的同一数量的简约的加法,除法则表现为其简约的减法,而且除法在一种情况下,即当除数是一个分数时,可化为同此分数的倒数相乘。代数的运算却进步了很多。每一个减法(a-b)都可以用加法(-b+a)来表示,每一个除法![]() 都可以用乘法
都可以用乘法![]() 来表示。至于幂运算,就更进步得多。运算方法的一切固定的差异都消失了,一切都可以用相反的形式表示出来。幂可以写做方根(x2=
来表示。至于幂运算,就更进步得多。运算方法的一切固定的差异都消失了,一切都可以用相反的形式表示出来。幂可以写做方根(x2=![]() ),方根可以写做幂(
),方根可以写做幂(![]() =x
=x![]() )。1被幂除或被方根除,可以写做分母的幂
)。1被幂除或被方根除,可以写做分母的幂![]() 一个数的几个幂相乘或相除,可以化为其各个指数的相加或相减。任何一个数都可以理解为并表示为任何其他一个数的幂(对数,y=ax)。[33]而这种从一个形式到另一个相反的形式的转化,并不是一种无聊的游戏,它是数学科学的最有力的杠杆之一,如果没有它,今天就几乎无法去进行一个比较困难的计算。如果从数学中哪怕只把负指数幂和分数指数幂取消掉,那么结果会怎样呢?
一个数的几个幂相乘或相除,可以化为其各个指数的相加或相减。任何一个数都可以理解为并表示为任何其他一个数的幂(对数,y=ax)。[33]而这种从一个形式到另一个相反的形式的转化,并不是一种无聊的游戏,它是数学科学的最有力的杠杆之一,如果没有它,今天就几乎无法去进行一个比较困难的计算。如果从数学中哪怕只把负指数幂和分数指数幂取消掉,那么结果会怎样呢?
(-·-=+,![]() =+,
=+,![]() 等等,应在前面说明。)
等等,应在前面说明。)
[120]
只有微分学才使自然科学能够用数学来表示过程即运动,而不仅仅表示状态。
[137]
分子和微分。维德曼(第3册第636页)149把有限的距离和分子的距离彼此直接对立起来。
[112]
量和质。数是我们所知道的最纯粹的量的规定。但是它充满了质的差异。(1)黑格尔,数目和单位,乘,除,乘方,开方。由此已经产生了黑格尔所没有强调的质的差异:质数和乘积,单根和幂。16不仅仅是16个1之和,而且也是4的2次方和2的4次方。不仅如此,质数使它和其他数相乘而得的数获得新的确定的质:只有偶数才能被2整除,类似的规定也适用于4和8。在用3做除数的情况下,有数字横和的规则。在用9和6做除数的情况下也是一样,但是在用6的情况下必须同时是偶数。在用7做除数的情况下有特殊的规则。数字游戏就建立在这上面,没有学过的人觉得莫名其妙。所以黑格尔(《量》第237页)关于算术的无思想性的说法是不正确的。但是参看《度量》150。
数学一谈到无限大和无限小,它就导入一个质的差异,这个差异甚至表现为不可克服的质的对立:量之间的差异太大了,以至它们之间不再有任何合理的关系,无法进行任何比较,它们变成在量上不可通约的了。例如,圆和直线通常是不可通约的,这也是一种辩证的质的差异;但是在这里正是同类数量的量的差异把质的差异提高到不可通约的地步。
[113]
数。单个的数在记数法中已经获得某种质,而且这要视记数法的情况而定。9不仅是1相加九次,而且是90、99、900000等等的基数。一切数的定律都依赖于并取决于所采用的记数法。在2进位记数法和3进位记数法中,2×2不等于4,而等于100或等于11。在以奇数作基数的每种记数法中,偶数和奇数的差异不复存在了,例如在5进位记数法中,5=10,10=20,15=30。同样,在这种记数法中,3的倍数3n的数字横和可以被3除尽的规则也失去作用了,9的情况也是这样(6=11,9=14)。因此,基数不但决定它自己的质,而且也决定其他一切数的质。
关于幂的关系,问题更进了一步:每个数都可以当做其他任何一个数的幂——有多少整数和分数,就有多少对数系统。
[116]
零是任何一个确定的量的否定,所以不是没有内容的。相反,零具有非常确定的内容。作为一切正数和负数之间的界限,作为可以既不是正又不是负的唯一真正的中性数,零不只是一个非常确定的数,而且它本身比其他一切以它为界限的数都更重要。事实上,零比其他任何一个数都有更丰富的内容。把它放在其他任何一个数的右边,按我们的记数法它就使该数变成原来的十倍。在这里,本来也可以用其他任何一个记号来代替零,但是有一个条件,即这个记号就其本身来说表示零,即等于0。因此,零本身的性质决定了零有这样的用处,而且唯有它才能够被这样应用。零乘任何一个数,都使这个数变成零;零除任何一个数,都使这个数变成无限大,零被任何一个数除,都使这个数变成无限小;它是和其他任何一个数都有无限关系的唯一的数。![]() 可以表现-∞和+∞之间的任何数,而且在每一种情况下都代表一个现实的量。——一个方程式的真实内容,只有当它的所有各项都被移到一边,从而把它的值约简为零时,才能清楚地表现出来,这在二次方程式中已是如此,而在高等代数学中几乎是一般的规则。一个函数F(x,y)=0,同样可以使之等于z,而这个z虽然等于0,却可以像普通的因变量一样被微分,而且可以求得它的偏微商。
可以表现-∞和+∞之间的任何数,而且在每一种情况下都代表一个现实的量。——一个方程式的真实内容,只有当它的所有各项都被移到一边,从而把它的值约简为零时,才能清楚地表现出来,这在二次方程式中已是如此,而在高等代数学中几乎是一般的规则。一个函数F(x,y)=0,同样可以使之等于z,而这个z虽然等于0,却可以像普通的因变量一样被微分,而且可以求得它的偏微商。
但是,任何一个量的无,本身还是有量的规定的,并且仅仅因此才能用零来运算。一些数学家心安理得地以上述方式用零进行运算,即把零当做特定的量的观念而用于运算,使它和其他量的观念发生量的关系,而当他们看到黑格尔把这一点概括成某物的无是一个特定的无[34]时,却大惊失色。
现在来谈(解析)几何。在这里零是一个特定的点,从这个点起,一条直线上某一方向定为正,而相反的方向定为负。因此,在这里零点不仅和表示某一正量或负量的任何点同样重要,而且比所有这些点更重要得多:它是所有这些点所依存、所有这些点与之发生关系、所有这些点由之决定的一点。在许多情况下,这个点甚至可以任意选定。但是一经选定,它就始终是全部运算的中心点,甚至常常决定其他各点(横坐标终点)所在的线的方向。例如,如果我们为了求得圆的方程式而选择圆周上的任何一点作为零点,那么横坐标轴必定通过圆心。这一切在力学中也得到应用,在那里,在计算运动时,每次选定的零点都构成整个运算的轴心。温度表上的零点是一个温度段的十分确定的下限,这个温度段可以任意分成若干度数,从而既可以用做这一温度段内各温度等级的量度,也可以用做更高温度或更低温度的量度。因此,零点在这里也是一个极其重要的点。甚至温度表上的绝对零点也决不代表纯粹的、抽象的否定,而是代表物质的十分确定的状态,即一个界限,一旦达到这个界限,分子独立运动的最后痕迹便消失了,而物质只是作为质量起着作用。总之,无论我们在什么地方碰到零,它总是代表某种十分确定的东西,而它在几何学、力学等等中的实际应用又证明:作为界限,它比其他一切以它为界限的现实的量都更加重要。
[117]
一。再没有什么东西看起来比这个数量单位更简单了,但是,只要我们把它和相应的多联系起来,并且按照它从相应的多中产生出来的不同方式加以研究,就知道再没有什么比一更为多样化了。一首先是整个正负数系统中的基数,它自身不断相加可得出其他任何数目。——一可以表示一的所有正指数幂、负指数幂和分指数幂:12,![]() ,1-2都等于一。——一是分子和分母相等的一切分数的值。——一可以表示任何数的零次幂,因此,它是在所有对数系统中其对数都相同即都等于零的唯一的数。这样,一是把所有可能的对数系统分成两个部分的界限:如果底大于一,则一切大于一的数的对数都是正的,而一切小于一的数的对数都是负的;如果底小于一,则结果相反。因此,如果说,任何数只要是由相加起来的一所组成,因而自身包含着一,那么,一自身也同样包含着其他一切数。这不仅就可能性来说是这样,因为我们单纯用一就能构成任何数;而且就现实性来说也是这样,因为一是其他任何数的特定的幂。数学家们只要觉得合适,便不动声色地在自己的计算中引用x0=1,或引用分子和分母相等的分数,即其值等于一的分数,因而在数学上应用包含在一中的多。可是,当人们按一般的说法对这些数学家讲,一和多是不可分的、相互渗透的两个概念,一寓于多中,同样,多也寓于一中,他们就会皱起鼻子,变起脸来。但是,只要我们一离开纯粹数的领域,就会看到情形确实如此。在测量长度、面积和体积时就已经看到,我们可以把相应量纲的任何数量当做单位,而在测量时间、重量和运动等等时也是如此。用于测量细胞,毫米和毫克还嫌太大;用于测量星球距离或光的速度,千米也嫌太小而不便使用,正如测量行星的质量,尤其是太阳的质量,千克也嫌太小了。这里清楚地表明,在这个乍看起来十分简单的单位概念中包含着何等的多样性和多。
,1-2都等于一。——一是分子和分母相等的一切分数的值。——一可以表示任何数的零次幂,因此,它是在所有对数系统中其对数都相同即都等于零的唯一的数。这样,一是把所有可能的对数系统分成两个部分的界限:如果底大于一,则一切大于一的数的对数都是正的,而一切小于一的数的对数都是负的;如果底小于一,则结果相反。因此,如果说,任何数只要是由相加起来的一所组成,因而自身包含着一,那么,一自身也同样包含着其他一切数。这不仅就可能性来说是这样,因为我们单纯用一就能构成任何数;而且就现实性来说也是这样,因为一是其他任何数的特定的幂。数学家们只要觉得合适,便不动声色地在自己的计算中引用x0=1,或引用分子和分母相等的分数,即其值等于一的分数,因而在数学上应用包含在一中的多。可是,当人们按一般的说法对这些数学家讲,一和多是不可分的、相互渗透的两个概念,一寓于多中,同样,多也寓于一中,他们就会皱起鼻子,变起脸来。但是,只要我们一离开纯粹数的领域,就会看到情形确实如此。在测量长度、面积和体积时就已经看到,我们可以把相应量纲的任何数量当做单位,而在测量时间、重量和运动等等时也是如此。用于测量细胞,毫米和毫克还嫌太大;用于测量星球距离或光的速度,千米也嫌太小而不便使用,正如测量行星的质量,尤其是太阳的质量,千克也嫌太小了。这里清楚地表明,在这个乍看起来十分简单的单位概念中包含着何等的多样性和多。
[69]
零次幂。在对数序列![]() log中,零次幂是很重要的。一切变数都会在某个地方经过一;因此,如果x=0,那么以变数作为指数的常数ax=1。a0=1所表现的,不外是和a的幂序列的其他各项联系起来去理解的一,只有在这种情形下这才有意义,才能得出结果
log中,零次幂是很重要的。一切变数都会在某个地方经过一;因此,如果x=0,那么以变数作为指数的常数ax=1。a0=1所表现的,不外是和a的幂序列的其他各项联系起来去理解的一,只有在这种情形下这才有意义,才能得出结果![]() 151,否则就不成。由此可知:尽管一看起来和自身多么等同,它本身却包含着无限的多样性,因为它可以是其他任何一个数的零次幂;这种多样性决不是纯粹虚构的,凡是一被看做确定的一,被看做和某个过程相联系的该过程的可变的结果之一(被看做某一变数的暂时的数值或形式)的时候,都会得到证明。
151,否则就不成。由此可知:尽管一看起来和自身多么等同,它本身却包含着无限的多样性,因为它可以是其他任何一个数的零次幂;这种多样性决不是纯粹虚构的,凡是一被看做确定的一,被看做和某个过程相联系的该过程的可变的结果之一(被看做某一变数的暂时的数值或形式)的时候,都会得到证明。
[118]
![]() [35]。——代数学上的负数,只是对正数而言,只是在和正数的关系中才是实在的;在这种关系之外,就其本身来说,它们纯粹是虚构的。在三角学、解析几何以及以这两者为基础的高等数学的某些分支中,它们是表示和正的运动方向相反的一定的运动方向;但是,不论从第一象限或第四象限都同样能计算出圆的正弦和正切,这样就可以把正和负直接颠倒过来。同样,在解析几何中,圆中的横坐标从圆周或从圆心开始都能够被计算出来,而且,在一切曲线中,横坐标都能够从通常定为负的方向上的曲线,[或者]从任何其他方向上的曲线被计算出来,并得出正确的、合理的曲线方程式。在这里,正只是作为负的补充而存在,反之亦然。但是代数学的抽象把负数当做独立的实数,即使是在和某些较大的正数的关系之外,也是如此。
[35]。——代数学上的负数,只是对正数而言,只是在和正数的关系中才是实在的;在这种关系之外,就其本身来说,它们纯粹是虚构的。在三角学、解析几何以及以这两者为基础的高等数学的某些分支中,它们是表示和正的运动方向相反的一定的运动方向;但是,不论从第一象限或第四象限都同样能计算出圆的正弦和正切,这样就可以把正和负直接颠倒过来。同样,在解析几何中,圆中的横坐标从圆周或从圆心开始都能够被计算出来,而且,在一切曲线中,横坐标都能够从通常定为负的方向上的曲线,[或者]从任何其他方向上的曲线被计算出来,并得出正确的、合理的曲线方程式。在这里,正只是作为负的补充而存在,反之亦然。但是代数学的抽象把负数当做独立的实数,即使是在和某些较大的正数的关系之外,也是如此。
[114]
数学。把某个确定的数,例如把一个二项式,化为无穷级数,即化为某种不确定的东西,从常识来说,这是荒谬的。但是,如果没有无穷级数和二项式定理,那我们能走多远呢?
[68]
渐近线。几何学开始于下列发现:直线和曲线是绝对对立的,直线根本不能用曲线表示,曲线也根本不能用直线表示,两者是不可通约的。但是,连圆的计算也只有用直线来表示它的圆周时才有可能。而在具有渐近线的曲线的情形下,直线完全化为曲线,曲线完全化为直线;平行的观念也同样趋于消失:两条线并不是平行的,它们不断地互相接近,但永远不相交。曲线的臂越伸越直,但永远不能完全变成直线,正如在解析几何中直线被看做曲率无限小的一次曲线一样。而不论对数曲线的-x变得多么大,y始终不会等于0。
[70]
直线和曲线在微分中终于等同起来了:在以弧的微分构成自己的斜边(用切线法)的微分三角形中,我们可以把这个斜边看做
“既是弧的要素又是切线的要素的一条小直线”,——不管我们把曲线看做由无限多的直线所构成,还是“看做真正的曲线;因为在每个M点上曲率既然是无限小的,所以曲线要素和切线要素的最后关系显然是等同的关系”。
在这里,关系虽然不断地接近等同的关系,但是根据曲线的本性来说这种接近是渐近的,因为相切处局限在一个无长度的点上,不过最后还是可以假定,直线和曲线的等同是达到了。(波绪《微积分》共和六年巴黎版第1卷第149页)在极曲线[36]中,虚构的微分横坐标甚至被假定和实在的横坐标平行,并根据这个假定进行运算,虽然两者相交于极上;由此甚至推论出两个三角形的相似性,其中一个三角形有一个角刚好在这样两条线的交点上,而这两条线的平行却是整个相似性的基础!(图17)152[37]
[139]
三角学。在综合几何学从三角形本身详述了三角形的性质并且再没有什么新东西可说之后,一个更广阔的天地被一个非常简单的、彻底辩证的方法开拓出来了。三角形不再被孤立地只从它本身来考察,而是和另一种图形,和圆联系起来考察。每一个直角三角形都可以看做一个圆的附属物:如果斜边=r,则两条直角边分别为正弦和余弦;如果其中的一条直角边=r,则另一条直角边=正切,而斜边=正割。这样一来,边和角便得到了完全不同的、特定的相互关系,如果不把三角形和圆这样联系起来,这些关系是决不能发现和利用的。于是一种崭新的三角理论发展起来了,它远远地超过旧的三角理论而且到处可以应用,因为任何一个三角形都可以分成两个直角三角形。三角学从综合几何学中发展出来,这对辩证法来说是一个很好的例证,说明辩证法怎样从事物的相互联系中理解事物,而不是孤立地理解事物。
[119]
数学的应用:在固体力学中是绝对的,在气体力学中是近似的,在液体力学中已经比较困难了,在物理学中多半是尝试性的和相对的,在化学中是具有最简单本性的简单的一次方程式,在生物学中=0。
[142]

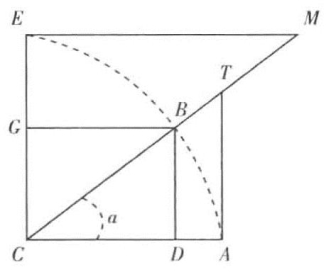
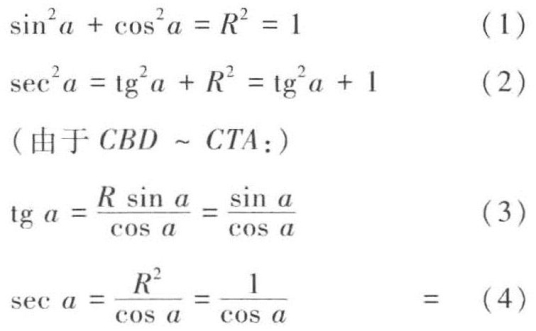
(由于CBD~CBG~CME:)
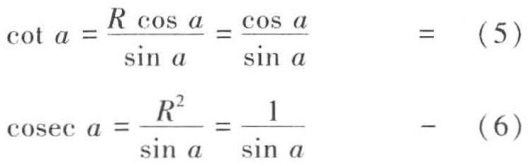
由于(CTA~CME),(3)乘以(5)得
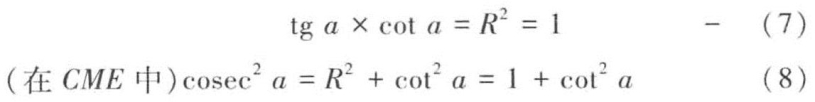
由(4)和(2)得
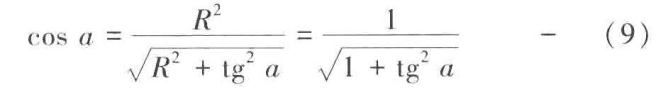
由(3)得
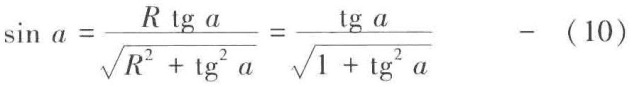
在每一个三角形中
(a、b、c是[与角A、B、C]相对的边)
sin(a±b)=sinacosb±sinbcosa
cos(a±b)=cosacosb∓sinasinb
因此 sin(2a)=2sinacosa
cos(2a)=cos2a-sin2a=2cos2a-1=1-2sin2a(r×r2=1)
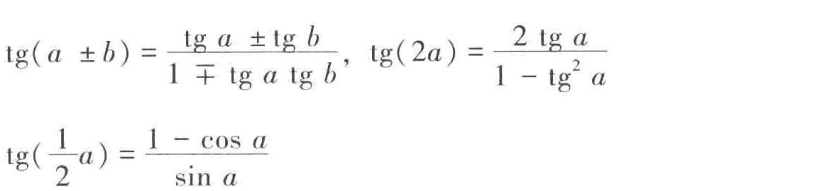
[143]
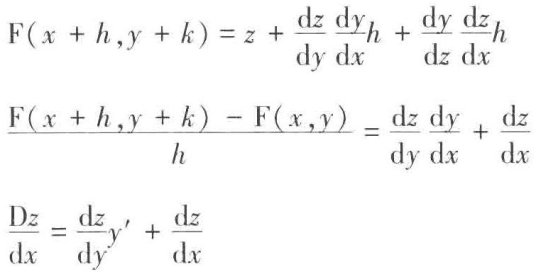
z=F(x,y);间接前提是x变成x+h,则
F(x+h,y)=(泰勒展开)![]() ……;再让y变成y+k,则
……;再让y变成y+k,则
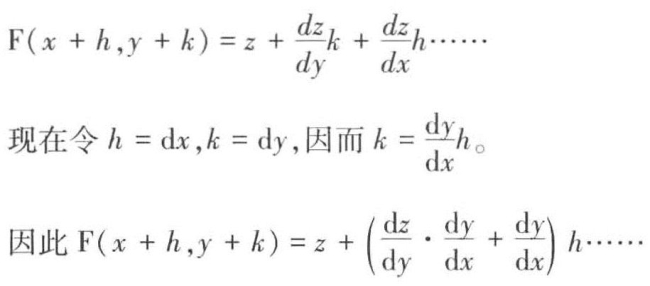
F(x+h,y+k)-z(或F(x,y))=上式右边去掉z。
两边除以h,或者dx,我们得到