[力学和天文学]
[63]
辩证思维的必要性的例子和自然界中非固定的范畴和关系的例子:落体定律,它在物体下落数分钟时便不正确了,因为这时不能再假设地球的半径=∞而毫无误差了,而且地球的引力在增大,而不像伽利略的落体定律所假定的那样保持不变。尽管如此,现在学校里还在继续讲授这个定律,而对保留条件却避而不谈!
[7]
牛顿的引力和离心力——形而上学思维的例子:问题没有解答,而只是提出,然而却被当做答案来讲授。克劳修斯的热的消散的见解也是如此153。
[34]
牛顿的万有引力。能够给予它的最好的评价就是:它不是解释而是描述行星运动的现状。运动是既定的。太阳的引力也是既定的。应当怎样用这些数据来解释运动呢?用力的平行四边形,用一种切线力来解释,这种切线力现在已成为我们不得不采用的必要假定。这就是说,如果我们以现有状态的永恒性为前提,我们就需要有一个第一推动,上帝。但是,现有的行星状态并不是永恒的,而运动原初也不是复合的,而是简单的旋转,力的平行四边形用在这里是错误的,因为它不只是要说明尚待发现的未知数x,就是说,牛顿所要求的,不只是提出问题,而且还要解答问题。
[74]
牛顿的力的平行四边形在太阳系中至多在环行天体分离出来的一刹那间是正确的,因为这时的旋转运动自身处于矛盾之中,它一方面表现为引力,另一方面又表现为切线力。但是,只要分离一完成,运动又重新成为统一的。这种分离必然会发生,这是辩证过程的证据。
[8]
拉普拉斯的理论只是以运动着的物质为前提——悬浮在宇宙空间中的一切物体都必然旋转。
[91]
梅特勒,恒星154。
哈雷在18世纪初叶,根据依巴谷和弗拉姆斯蒂德两人关于三颗星的报告之间的差异,首先得出了星体自行的观念(第410页)。——弗拉姆斯蒂德的《不列颠星表》[38]是第一本比较精确、比较完备的星表(第420页);后来在1750年前后有布拉德莱、马斯基林和拉朗德的观测。
关于巨大天体的光线射程的荒唐理论和梅特勒据此所作的推算,与黑格尔《自然哲学》[39]中的某种东西一样荒唐(第424—425页)。
恒星最大的自行(可见的)每百年为701″=11′41″=太阳直径的![]() 从天文望远镜中观测到的921颗星的自行的最小平均值是8.65″,个别的为4″。
从天文望远镜中观测到的921颗星的自行的最小平均值是8.65″,个别的为4″。
银河——一系列的环,它们都有一个共同的重心(第434页)。
昴星团和其中的昴宿六(金牛座η),是“直到银河最远区域”的我们的宇宙岛的运动中心(第448页)。昴星团内部的公转周期平均约为200万年(第449页)。在昴星团周围,星多和星少的环状星团交替出现。——赛奇对于现在就把一个中心确定下来的可能性提出异议。
据贝塞尔说,天狼星和南河三星除一般的运动之外,还在环绕某一暗体的轨道上运行(第450页)。大陵五食,每3天一次,持续8小时,是由光谱分析证实的(赛奇,第786页)。
在银河区域中,然而是在它的深远的内部,有一个由7到11等星组成的稠密的环;在远离这个环之外的地方是一些同心的银河环,我们能看见其中的两个。据赫歇尔说,在银河中,用他的天文望远镜所能看到的星约有1800万个,位于环内的星约有200万个或更多,就是说总共超过2000万个。此外,在银河本身中,在已经分辨出来的星的背后,始终存在着一种无法分辨的微光,因此很可能还有一些更遥远的、隐而不见的星环吧?(第451—452页)
昴宿六距太阳573光年。由能够看见的各星体组成的银河环的直径,至少为8000光年。(第462—463页)
在以太阳到昴宿六的距离573光年为半径的范围内运动着的天体的质量,共计是11800万个太阳质量(第462页);这和在其中运动着的至多200万个星体是完全不符合的。有暗体吗?这里无论如何有点错误。这证明我们的观测的先决条件还是多么不完备。
梅特勒假定银河环最外端的距离为几万光年,也许为几十万光年(第464页)。
一个反对所谓光的吸收的绝妙理由:
“当然存在着这样的距离〈从那里再也没有任何光能达到我们这里〉,然而理由却完全不同。光的速度是有限的;从创世之初直到现在,消逝的是一段有限的时间,因此我们只能看到光在那段有限时间里所经过的距离以内的天体!”(第466页)
光既然与距离的平方成比例地减弱,它就必定会达到一点,在这一点上,我们的眼睛,不管它们如何敏锐和配上什么样的装备,都再也看不见光了,这是不言而喻的;这已经足以驳倒奥伯斯的见解:只有用光的吸收才能说明,为什么四面八方、远及无限距离都充满着发光星体的天空会是昏暗的。但这决不是说,并不存在这样一个距离,一到这个距离,以太便不再让光通过了。
[92]
星云。它有各种形状:轮廓分明的,圆的,椭圆的,或不规则的和锯齿状的。它有各种程度的可分辨性,直到模糊得完全不可分辨,只能识别出趋向中心的密集。在一些可分辨的星云中,可以看见的达1万颗星,中心多半是比较密集的,很难得有一颗较明亮的中心星。罗斯的巨型天文望远镜又分辨出许多星云。老赫歇尔数出了197个星群和2300个星云,此外还应加上小赫歇尔在南天星表中所记录的星云。不规则的星云必定是遥远的宇宙岛,因为云雾体只能以球体或椭圆体的形式处于平衡状态。这些星云大多数甚至在最高倍的天文望远镜中也只是刚刚能看到。圆形的星云或许可能是云雾体,在上述的2500个星云中有78个是这种云雾体。至于它们和我们的距离,赫歇尔假定是200万光年,梅特勒——在星云的实际直径=8000光年这个假定下——假定是3000万光年。因为每个天体体系和最近的天体体系的距离,至少是这些天体体系的直径的100倍,所以我们这个宇宙岛和最近的宇宙岛的距离,至少应该是8000光年的50倍=40万光年,这样一来,在存在着数千星云的情况下,我们就远远超出老赫歇尔的200万光年了([梅特勒,第485—]492页)。
赛奇:
可分辨的星云提供了连续的和普通的恒星光谱。但是本来意义上的星云“有一部分提供了连续的光谱,例如仙女座中的星云,而大多数则提供了由一条或很少几条亮线所组成的光谱,例如猎户座、人马座和天琴座中的星云,以及许许多多以行星状〈略带圆形的〉星云著称的星云”(第787页)。
(根据梅特勒的说法,第495页,仙女座中的星云是不可分辨的。——猎户座中的星云是不规则的,呈棉絮状,而且像胳膊一样伸出去!第495页——天琴座中的星云呈环状,略带椭圆形,第498页。)
哈金斯在第4374号(赫歇尔星表)星云的光谱中发现了三条亮线,“由此立即推论出:这个星云并不是由单个的星体所组成的星群,而是一个真正的星云,是气体状态的炽热的实体”[第787页]。
这三条线中,一条属于氮,一条属于氢,第三条未知。猎户座中的星云的情况也是一样。甚至含有发光点的星云(长蛇座和人马座)也有这些亮线,因此密集中的星体的物质还不是固态或液态(第789页)。天琴座的星云只有一条氮线(第789页)。——猎户座的星云最密集的地方是1°,全部广延是4°[第790—791页]。
[93]
赛奇:天狼星:(https://www.daowen.com)
“11年以后〈即贝塞尔的计算11年后,梅特勒,第450页〉……不但发现了天狼星的卫星,一颗自己发光的6等星,而且还证实了它的轨道也和贝塞尔所计算的相符合。南河三星及其伴星的轨道现在已由奥沃斯确定了,但是这颗卫星本身还没有观察到。”(第793页)
赛奇:恒星。
“因为恒星除了两三个例外,都没有可觉察到的视差,所以它们离我们至少”有30多光年之远(第799页)。
据赛奇说,(赫歇尔的大望远镜还能分辨出的)16等星离我们有7560光年之远,而罗斯的望远镜所能分辨出的,至少有20900光年之远(第802页)。
赛奇自问道(第810页):
当太阳和整个太阳系死灭的时候,“自然界中是否存在着力量能把死了的星系恢复到最初的炽热的星云状态,并使它再度获得新的生命呢?我们不知道”。
[177]
潮汐摩擦。康德和汤姆生—泰特
地球的自转和月球的引力155
汤姆生和泰特《自然哲学论》第1卷第191页(第276节):
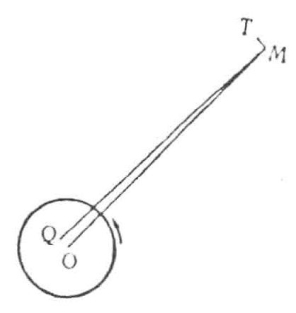
“凡像地球这样有一部分自由表面被液体覆盖着的天体,都存在来自摩擦的间接的阻抗,这种摩擦阻碍着潮汐运动。当这些天体和邻近的天体相对运动时,这些阻抗必定总是从它们的相对运动中不断吸取能量。如果我们首先单独考察月球对地球及其海洋、湖泊、河流的作用,我们就会看到,这个作用势必使地球绕自己的轴而自转的周期和这两个天体绕它们的惯性中心而旋转的周期相等;因为只要这两个周期不相同,地球表面的潮汐作用必然从这两个天体的运动中不断吸取能量。为了比较详细地考察一下这个问题,同时为了避免不必要的麻烦,我们假设月球是一个匀称的球体。月球质量和地球质量之间引力的相互作用和反作用,相当于沿某条经过月球中心的直线起作用的单独的力,而且只要地球自转的周期小于月球绕地球运动的周期,这个力就阻碍地球的自转。因此,它必定沿着MQ这条线发生作用,因而偏离地心OQ这样一段距离;这个偏离在示意图中当然是被大大扩大了。现在,沿直线MQ实际作用于月球的力可以设想是由两股力合成的,一股是沿着指向地心的直线MO发生作用,其大小和整个力差不多相等,另一股是相对说来甚小的力,它沿着垂直于MO的直线MT起作用。后一股力极接近于和月球的轨道相切,其作用和月球的运动是同向的。如果这个力突然开始发生作用,它首先会使月球的运行速度加快;经过一段时间,月球就会由于加速运行而同地球拉开一段距离,这使得它(由于它是抵抗着地球的引力而运动的)正好失去它从切线加速力所得来的速度。持续不断的切线力顺着运动方向发生作用,但是它的量很小,每一瞬间只能导致和圆形轨道稍有偏离。这种切线力的作用就在于,它会逐渐拉大卫星和中心天体的距离,并且抵抗中心天体的引力做功,而它所做的功又等于运动失去的动能。如果想象这个环绕中心天体的运动是沿着极其缓慢地扩展着的螺旋形轨道运行的,问题就容易理解了。假设力和距离的平方成反比,那么重力的反运动方向的切线分力,将是顺运动方向的起干扰作用的切线力的两倍,因此,抵抗前者所做的功,有一半是由后者做的,而另一半则是从运动中吸取来的动能做的。我们现在所考察的起干扰作用的特殊原因对月球运动所发生的全部作用,很容易由动量矩原理求出。我们看到,地球的惯性中心和月球的惯性中心相对于它们共同的惯性中心而运动,由它们的运动随时得到的动量矩,等于地球绕自己的轴自转而损失的动量矩。处于现今运动状态的月球的惯性中心和地球的惯性中心的动量矩之和,约为现今地球自转的动量矩的4.45倍。前一个运动的平均平面是黄道面,所以两个动量的轴互成23°27.5′的平均倾角,如果略去太阳对月球运动平面的影响,这个角度就可以看做两个轴现今的实际的交角。因此,合成的或总的动量矩为现今地球自转的动量矩的5.38倍,其轴和地轴成19°13′交角。所以落潮和涨潮最终导致地球和月球以这个合成的动量矩围绕这个合成的轴作简单的等速转动,就好像它们是同一个刚体的两个部分一样:在这种条件下,月球和地球问的距离会(大约)按1∶1.46的比例(即两个惯性中心现今的动量矩的平方与总的动量矩的平方之比)加大,而公转的周期则按1∶1.77的比例(即这两个动量矩的立方之比)加大。因此,距离会增大到347100英里,而周期会延长到48.36天。假如宇宙中除了地球和月球不再有其他的天体,那么这两个天体就会沿圆形轨道围绕它们共同的惯性中心永远这样运行下去,而地球则以同一周期围绕自己的轴旋转,结果总是以同一个面朝向月球,因而地球表面的全部液体部分对于其固体部分来说处于相对的静止状态。但是太阳的存在使得这种状态不能永久保持下去。地球上会发生太阳潮——在地球相对太阳旋转的一个周期中有两次潮涨和两次潮落(也就是说,在一个太阳日内有两次,或者在一个月内也是如此)。如果不是因为液体的摩擦会使能量有所丧失,这种情况是不可能发生的。要把地球和月球运动中由这种原因所造成的干扰的整个过程描绘出来是不容易的,但是这种干扰归根到底会导致这样的结果:地球、月球和太阳像一个刚体的各个部分一样围绕它们共同的惯性中心旋转。”
1754年,康德首先提出了这样的观点:地球自转因潮汐摩擦而放慢,并且这种作用只是在这样的时候才会完结:
“那时,它〈地球〉的表面和月球将处于相对静止之中,也就是说,它围绕自己的轴旋转的周期将和月球围绕地球旋转的周期相等,结果将总是以同一个面朝向月球。”[40]
同时,他认为,地球自转的变慢仅仅起因于潮汐摩擦,即地球上有液体存在。
“如果地球完全是固体,没有任何液体,那么无论太阳的引力还是月球的引力,都不会改变它绕轴的自由旋转,因为这种引力对地球的东西两个部分的吸引力是相同的,因而不会引起向哪一方偏斜;所以,它一点也不妨碍地球继续完全自由地自转,就好像没有受到任何外来的影响一样。”[41]
对于这样的成果,康德应当感到满足。要更深入地了解月球对地球自转的影响,当时还缺少科学上的一切前提。的确,差不多过了一百年,康德的理论才得到公认;又过了一些时间,人们才发现,落潮和涨潮只是太阳和月球的引力对地球自转产生影响作用的一个明显的方面。
这个较为一般的见解由汤姆生和泰特在上文作了阐发。月球和太阳的引力不仅对地球或地球表面上的液体发生作用,而且对整个地球都发生作用,阻碍着地球的自转。只要地球自转的周期和月球围绕地球旋转的周期不一致,月球的引力(暂且只考察这种引力)的作用就会促使这两个周期彼此越来越接近。如果(相对的)中心天体自转的周期比卫星公转的周期长,那么前者会逐渐缩短;如果前者较短,就像地球的情形那样,那么它会变长。但是,动能不可能在一种情况下凭空产生,也不可能在另一种情况下归于消灭。在前一种情况下,卫星越来越接近中心天体,它的公转周期逐渐缩短;在后一种情况下,它离中心天体越来越远,公转周期变长。在前一种情况下,卫星由于接近中心天体而失去的位能,正好等于中心天体由于自转速度加快而得到的动能;在后一种情况下,卫星由于和中心天体的距离加大而得到的位能,正好等于中心天体所失去的自转的动能。地月系统中所存在的动力学能量,即位能和动能的总和不变;这个系统完全是保守的。
可见,这个理论和所考察的天体的物理化学性质完全无关。它是从自由天体的一般运动规律中得出的,这些天体之间的联系是由同质量成正比而同距离的平方成反比的引力所确立的。这一理论显然是作为康德的潮汐摩擦理论的一般化而产生的,并且汤姆生和泰特在这里甚至是把它当做对后一理论的数学论证向我们表述的。但是实际上它把潮汐摩擦这种特殊情况排除在外了。令人奇怪的是,对于这一点,这两位作者连想也没有想到。
摩擦是物体运动的障碍,几百年来都被看做是物体运动的消灭,即动能的消灭。现在我们知道,摩擦和碰撞是动能借以转化为分子能,转化为热的两种形式。因此,每当发生摩擦时,动能本身就失掉,可是又再现出来,但不是作为动力学上的位能,而是作为热这一特定形式的分子运动。可见,由于摩擦而失掉的动能,从所考察的系统的动力学方面来说,暂时确实是失掉了。只有当它从热的形式反过来又转化为动能时,才能重新起动力学意义上的作用。
那么,潮汐摩擦的情况又是怎样的呢?显然,由月球的引力传给地球表面的水的全部动能,在这里也转化为热,这或者是由于水的粘滞性所造成的水的各个质点的相互摩擦,或者是由于水与地球固体表面的摩擦和阻抗潮汐运动的岩石的破碎。在这些热中,只有促进水面蒸发的微不足道的一部分反过来又转化为动能。但是,整个地月系统传给地球表面某一个部分的这点微不足道的动能,也会暂时留在地球表面上,经受那里起作用的各种条件的影响,而这些条件则给活动在地球表面上的一切能量准备了同一个最终命运:最后转化为热并放射到宇宙空间中去。
可见,就潮汐摩擦无可辩驳地阻碍地球的自转而言,这方面耗费的动能,对于地月动力学系统来说,是绝对地失掉了。所以,它不能以动力学上的位能的形式在这个系统内部再现。换句话说,由于月球的引力而在阻碍地球自转方面耗费的动能,只有对地球上的固体发生作用的那一部分,能够作为动力学上的位能完全再现,也就是能够通过月球距离的相应拉大而得到抵偿。至于对地球上的液体发生作用的那一部分动能,只有当它不使这些液体本身按同地球自转相反的方向运动时,才可能是这样,因为这种运动会完全转化为热,并由于放射出去而从系统中最终失去。
关于地球表面的潮汐摩擦的情况,也同样适用于有时作为假说提出的假想的流体地心的潮汐摩擦。
这里颇为奇怪的是,汤姆生和泰特竟没有注意到,他们为了论证潮汐摩擦理论却提出了以下面这个默认的前提为出发点的理论,这个前提就是:地球是一个完完全全的刚体,决不可能有潮汐,因而也不可能有潮汐摩擦。
[155]
笛卡儿发现,落潮和涨潮都是由月球的作用所引起的。他还和斯涅尔同时发现了光的折射的基本定律(沃尔夫在第325页上对此提出异议156),并且以他所特有的、和斯涅尔不同的方式来表述这一定律。
[62]
迈尔《热力学》[42]第328页:康德已经讲过,落潮和涨潮对旋转的地球施加起延缓作用的压力(根据亚当斯的计算,恒星日的长度现在每千年增加百分之一秒)。
[140]
动力学中动能本身的消耗总是两重性的,并且有两重结果:(1)做出的运动功,相当量的位能的产生,但是这个量总是小于用掉的动能;(2)摩擦等等阻抗(重力除外)的克服,这些阻抗把所消耗的动能的剩余部分转化为热。——在转化回来时也是如此:依转化的方式不同,由摩擦等等而损失的一部分作为热消散了。——这一切全是老生常谈!
[154]
碰撞和摩擦。力学把碰撞的作用看做是纯粹地发生的。但是实际上并不是这样。在每次碰撞时,都有一部分机械运动转化为热,而摩擦无非是碰撞的一种形式,它不断地把机械运动转化为热(摩擦取火在远古时就已经为人所知)。
[10]
摩擦和碰撞使有关的物体产生内在的运动,即分子运动,后者视情况区分为热、电等等。然而这种运动只是暂时的,无因便无果。在一定的阶段上,这一切会转变为永久的分子变化,即化学变化。
