我国房地产价格与通货膨胀关系实证分析
通过上述房地产价格与通货膨胀关系的理论分析可知，房地产价格与通货膨胀之间的存在复杂、间接的关系，本节通过非结构化的非平稳面板计量方法，对我国近十年来房地产价格与通货膨胀之间的关系进行实证分析。面板数据以及面板计量方法的使用，不仅可以扩大样本量克服小样本带来的检验结果的不稳定性，同时还可以进行各城市之间的比较。
（一）指标选取和处理
房地产价格指数反映了不同时期房地产价格水平的变化趋势和程度的相对数量指标，目前国内覆盖全国的房价指数主要有中国房地产指数系统（简称“中房指数”）、全国房地产开发业务综合景气指数（简称“国房指数”）以及由国家发改委和国家统计局联合发布的全国35个大中城市房价指数。其中，国房指数价格和中房指数都没有提供较全面的国内各大城市的房屋价格指数。所以，本书选用全国35个大中城市房价指数中的房地产销售价格指数作为房价（HP）变量，各大中城市的城市居民消费价格指数（CPI）作为物价指数，数据来源于Wind数据库和中国资讯行（China InfoBank），删去数据缺失的部分城市，最终采用了全国30个大中城市从1998年第一季度至2009年第一季度的季度面板数据。由于房地产销售价格指数和CPI都是同比，本书对数据进行了调整，HP调整成以2004年第一季度为基期的定基环比数据，CPI调整成以2007年第一季度为1基期的定基环比数据。
首先对房价和CPI面板数据进行面板单位根检验，判断数据是否平稳。如果平稳则可直接根据数据性质进行固定效应模型或是随机效应模型的OLS回归，估计两者之间的影响系数；如果两组面板数据都是非平稳的，并且是具有同阶单位根，那么就要对它们进行面板协整检验，检验两者之间是否具有长期的均衡关系，并且利用面板DOLS进行系数的估计。最后，利用面板误差修正模型来分析房价与CPI之间的短期和长期Granger因果关系。
（二）实证分析
1.面板单位根检验
为增强检验结果的稳健性，我们同时采用LLC、Breitung、IPS、ADF-Fisher和PP-Fisher方法分别对房价和CPI的原序列和一阶差分进行面板数据单位根检验，并且对含截距和带时间趋势模型都进行了检验，以综合考虑各个统计检验的结果来检查这些数据是否平稳。表7.1给出了各面板数据单位根检验方法的检验结果。
表7.1 房价和房租的面板单位根检验结果
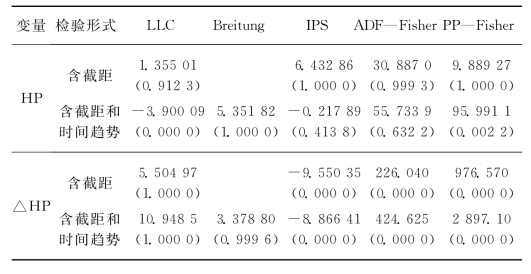
续 表
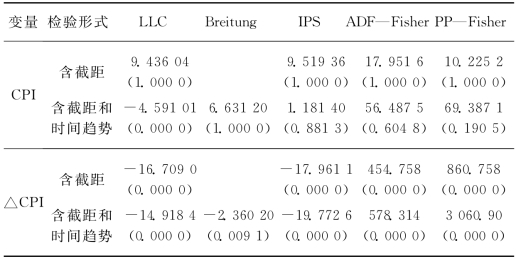
注：括号内报告了估计量的p值；所有检验方法的原假设H0为存在单位根。
从表7.1可以看出，房价的原序列面板单位根检验，每种方法含截距形式的检验都接受原假设，认为存在单位根，在含截距和时间趋势形式的检验中，除LLC和PP-fisher方法外，其他三种方法都接受原假设，所以我们可以认为房价原序列非平稳。房价序列一阶差分后，不管是含截距项还是既含截距项又带时间趋势形式，除LLC和Breitung方法外，其他三种方法都在1%显著水平下拒绝原假设，认为不存在单位根，因此我们认为房价的一阶差分序列平稳。对于CPI序列而言，原序列除含截距和时间趋势检验中LLC方法外，其他所有方法在含截距和既含截距又带时间趋势这两种形式的检验中，都接受原假设，认为CPI原序列非平稳。在CPI的一阶差分序列单位根检验中，每种方法在两种形式下的检验都拒绝原假设，认为房租的一阶差分序列平稳。所以，我国30个城市的房价和CPI的面板数据都是非平稳的，存在一阶单位根。
2.面板协整检验
我国30个城市的房价与CPI面板数据都为一阶单整，两者之间可能存在协整关系。为保证结论的可靠性，我们分别采用Pedroni的七个统计量来进行面板协整检验，结果如表7.2所示。从表7.2可以看出，七个统计量中除Pnael V方法外，其他所有检验方法的结果均在1%显著水平下拒绝原假设，认为房价和CPI之间存在协整关系，即房价与CPI之间存在长期、稳定的均衡关系。
表7.2 房价与房租的面板协整检验结果
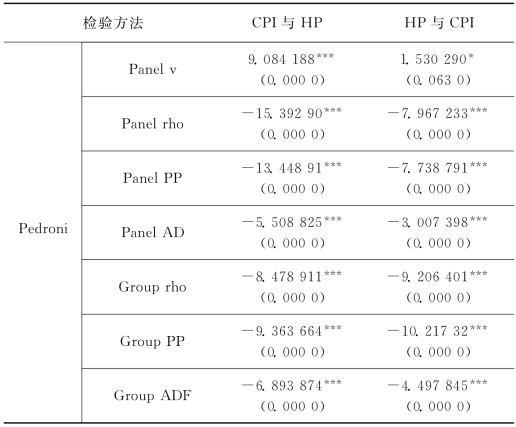
注：（1）表中Pedroni的七个检验的原假设H0都为不存在协整，在零假设下统计量服从渐近正态分布；（2）括号中报告了p值；（3）符号＊＊＊、＊＊、＊分别表示在1%、5%和10%的显著水平下拒绝原假设；（4）Pedroni检验设定中，认为没有时间趋势，使用SCI标准选择滞后阶数，Newey-west窗宽选择使用的是Bartlett核函数。
3.面板DOLS分析
接下来采用面板DOLS方法来估计我国房价与CPI之间的协整方程，即刻画两者之间的长期稳定的均衡关系。模型（1）和模型（2）中的
分别描述了房价对CPI的长期影响程度和CPI对房价的长期影响程度。系数
的面板DOLS估计结果如表7.3所示。
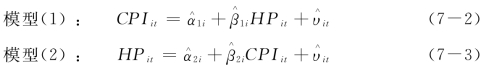
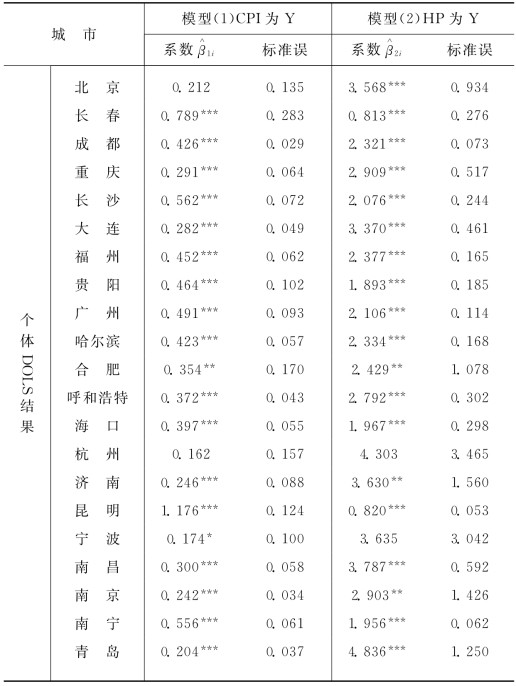
表7.3 房价与CPI长期均衡关系的面板DOLS系数估计结果
续 表
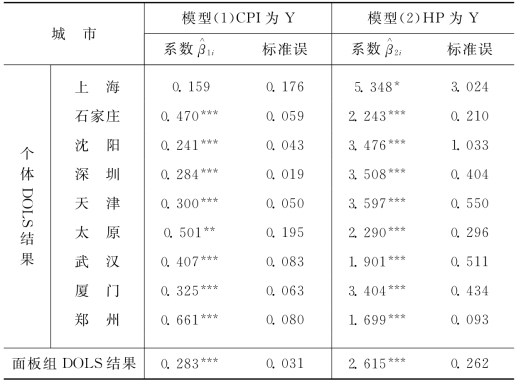
注：符号＊、＊＊、＊＊＊分别表示系数在10%、5%、1%显著性水平下显著。
从模型（1）的DOLS回归结果可以看出，系数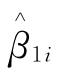
都为正且普遍显著，除北京、上海、杭州和宁波这四个房价涨速最快的城市系数不显著外。这表明长期来看，我国各大中城市的房价上涨普遍对CPI构成了上涨的压力。从模型（2）的DOLS回归结果来看，除长春和昆明两个城市外，其他城市的
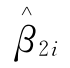系数普遍显著且大于1[3]，这表明我国各大中城市房地产通货膨胀具有对冲作用，房价上涨普遍能随着CPI的上涨。
4.面板Granger因果关系检验
由于房价与CPI之间存在协整关系，接下来使用面板误差修正模型（Panel Error Correction Model，PECM），采用Engle- Granger两步法，来检验我国房价和CPI之间的Granger因果关系检验。第一步是估计长期关系模型来获得残差项，第二步是使用动态面板误差修正来估计Granger因果关系，建立的面板误差修正模型为：
模型（3）：
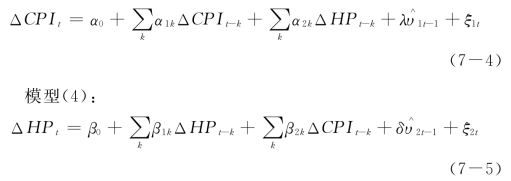
其中，Δ表示一阶差分；k表示滞后阶，本书采用的是房价和CPI的季度数据，所以k取值为0至4；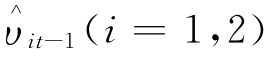
表示房价和CPI长期关系模型的残差项，即模型（1）和（2）的中的残差。依据Granger因果关系检验原理，在模型（3）中，如果ΔHP的滞后项的系数不全为0，则表示房价是CPI的短期Granger原因，我们可以通过设置原假设：H0：α2k＝0，
k来检验；相应地，模型（4）中CPI是否为房价的短期Granger原因的原假设为H0：β2k＝0，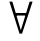
k。由于模型（3）和（4）中所有变量都是平稳的，所以可以用标准F统计量来检测原假设。λ和δ分别表示房价与CPI的短期偏离长期均衡的的调整力度，因此，我们可以通过系数λ和δ的有效性来检验房价与房租的长期Granger因果关系。
从表7.4模型（3）的回归结果可以看出，滞后一期和二期的房价增长对CPI的作用为负，但是不显著，从表7.5的F检验也可以看出，短期的房价变动对CPI的影响为负且不显著。λ系数显著且为负，说明CPI和房价的长期均衡关系对短期CPI变动具有修正作用。从模型（4）的回归结果可以看出，滞后一期的CPI变动对HP变动影响为正但不显著，滞后二期、三期和四期的CPI变动对HP变动具有负向作用，结合表7.5中的F检验结果可以看出，短期内CPI变动是HP变动的Granger原因。δ系数为正且不显著，说明房价和CPI的长期均衡关系对HP的波动没有修正关系。这与我国各大中城市房价上涨过快的事实是相符的。综上所述，短期来看，CPI是HP的Granger原因；但HP不是CPI的Granger原因；长期来看，HP是CPI的Granger原因，但CPI不是HP的Granger原因。
表7.4 面板误差修正模型回归结果
续 表
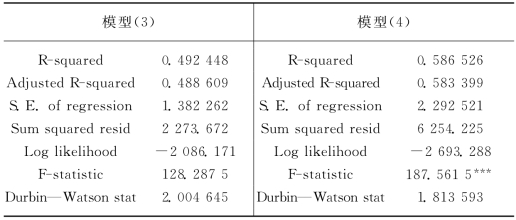
注：符号＊、＊＊、＊＊＊分别表示系数在10%、5%、1%显著性水平下显著；括号中报告的是t值。
表7.5 Granger因果关系检验
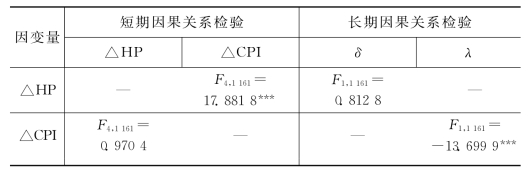
注：符号＊＊＊表示1%显著性水平下拒绝原假设。
（三）结论
通过以上30个城市的房价与CPI的面板单位根和面板协整的检验，以及面板DOLS模型和面板误差修正模型的估计，得出以下结论：（1）我国各大中城市的房价与CPI之间存在长期稳定的均衡关系，这种长期的均衡关系对短期的CPI具有一定的修正作用，但是对房价不具有修正作用。（2）长期来看，房价上涨对CPI上涨具有一定的正向压力，但短期来看，这种压力是负向的且影响不大。（3）长期来看，我国各大城市房地产具有很好的通货膨胀对冲能力，短期来看通货膨胀的变动对房价具有显著的影响。