4.2.2 边界条件和地震波动的输入
在进行数值计算时,计算模型的范围有限,这就需要人为地将计算区域与周围区域断开,在断开处就要用到人工边界。人工边界按照计算类型的不同可分为静力和动力人工边界。静力人工边界由来已久,形式较为简单,通常有固定边界、滚轴边界等。动力人工边界是根据波动在围岩介质中的传播过程推导出来的,经过几十年的发展,已形成多种施加人工边界的方法,但是总体来说可以分成全局人工边界和局部人工边界两大类别,并应用于各自适应的工程计算中[98]。
当前,在动力人工边界方面使用效果较好,使用最广泛的是黏弹性人工边界。黏弹性人工边界是由地震波动传播方程推导出来的[99]。
对于平面内的柱面波(以P波为例),其波动方程可以表示为
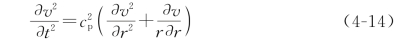
该波动方程的解可表达为
![]()
其中,g为任意函数。
经推导,可得任一半径rb处的应力,可用该处的速度和位移表示为
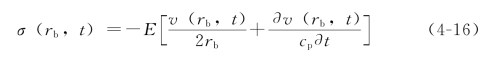
由波速计算公式可将式(4-16)表示为
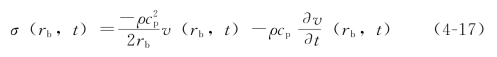
式中 v——波的位移函数;
cp——p波波速;
r——计算点至震源的距离;(https://www.daowen.com)
ρ——密度。
由式(4-17)可知,若在r=rb处断开结构,相当于在该处的法向和切向各施加一个弹簧和阻尼器(c=ρcp)并联的人工元件,可以满足原有的受力条件,这就是波动法使用的黏弹性人工边界,即黏弹性人工边界相当于在人工边界处通过施加等价弹簧和阻尼器来模拟地震波的传播。
为实现波动输入,在人工边界上施加总应力σz,采用力学中分离隔离体概念[100],将人工边界与附加其上的物理元件脱离,则总应力σz包括对边界施加的σ0使人工边界上的节点产生位移为v0的运动,还包括对物理元件上施加应力σ1(σ1=-σ)使节点的位移为v0,即
![]()
对P波入射
![]()
将式(4-17)、式(4-19)代入式(4-18),化简后得到
![]()
式中 k——黏弹性边界的等效弹性模量。
由式(4-20)可推导出需要在人工边界节点处施加的等效节点荷载的计算公式,进而可以在地下结构上施加等效节点荷载进行有限元计算,完成地下结构在地震荷载作用下的动力时程分析,本书即采用黏弹性人工边界进行动力有限元数值计算。
对于地震荷载,施加于底部边界的动力输入形式依地基条件的不同而有所区别,对于具有基岩的较坚硬的底部围岩条件可以采用地震波加速度时程的输入方式,对于底部岩体较软的情况一般采用波动力的方式施加,具体使用时需要进行计算对比后确定。
另外,对于输入地震荷载的特性也需要进行研究分析,可以选取实测的地震波时程或者采用人工合成的方式施加,地震波在使用之前还要进行地震级别调整、基线校正和频谱分析的处理工作。在进行数值计算分析或振动台模型试验前还要分析模型的频谱特性,研究模型和输入地震波的频谱特性的适应性,才能得到合理的结果。
至此,本书确定了进行隧道地震动力计算的数值计算模型。
